Файл: Городского округа г. Выкса Нижегородской области Графы в математике Физикоматематическое отделение Секция математическая.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 52
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Американский Фрэнк Харари (1921 – 2005) по праву считается основателем современной теории графов. Его 700 статей, выступления на конференциях в 87 странах, основанный им в 1977 году престижный «Журнал теории графов», вышедшая в 1969 году, считающаяся одной из самых значимых книг по этой теме, являются доказательством тому, что он заслужил международное признание. Он применял теорию графов не только в математике и информатике, но и в антропологии, географии, лингвистике, искусстве, музыке, физике, инженерном деле и других областях.
Голландский учёный Эдсгер Вибе Дейкстра (1930 – 2002) заинтересовался компьютерными программами в раннем детстве и посвятил им всю свою жизнь. Ему мы обязаны знаменитой фразой «Информатика не более наука о компьютерах, чем астрономия – наука о телескопах». Дейкстра никогда не пользовался компьютером, кроме как для отправки электронной почты и поиска информации в интернете, а все свои труды об алгоритмах и языках программирования он писал … от руки!
Пол Эрдёш (1913-1996) родился и получил образование в Будапеште. Благодаря выдающемуся уму он добился исключительных результатов в теории графов, комбинаторике, геометрии и теории чисел. Он стал автором множества удивительных задач и гипотез, а также написал свыше 1500 статей.
2.3. Азы теории графов
Граф определяется множеством точек (которые также называются вершинами, или узлами графа) и множеством ребер, или дуг графа, которые соединяют его вершины попарно.
Рис.1 Рис.2 Рис.3
На рисунке 1 представлен нулевой граф, состоящий из изолированных вершин; на рисунке 2 - полный граф с тремя вершинами и тремя рёбрами; на рисунке 3 - граф с шестью вершинами и восьмью рёбрами. Две вершины, соединенные ребром, называются смежными. Два ребра, которые имеют общую концевую вершину (инцидентные этой вершине), также называются смежными. Степенью вершины графа называется количество выходящих из нее ребер. В связи с этим, вершина, имеющая четную степень, называется четной вершиной, соответственно, вершина, имеющая нечетную степень, называется нечетной вершиной.
Если вершинам графа сопоставить буквы, числа или некую другую информацию, то говорят, что такой граф является помеченным. Если рёбрам графа поставлены в соответствие некие веса, такой граф называется взвешенным. Если на рёбра графа нанести стрелки, обозначающие направления, то эти ориентированные рёбра графа будут называться дугами. Если все рёбра являются ориентированными, то такой граф называется ориентированным, или орграфом. Графы также можно представить в виде списков, таблиц и различных выражений. Вершины графа можно изобразить в виде точек, окружностей, треугольников, а рёбра - в виде прямых, отрезков или фигурно изогнутых линий. Учитывая подобное разнообразие, важно уметь определять, когда два представления графа являются эквивалентными (изоморфными). Эквивалентные представления графа содержат одинаковые вершины и одинаковые связи между ними. Иными словами, между вершинами и рёбрами двух представлений должно существовать взаимно однозначное соответствие, такое, что степени вершин в обоих случаях будут одинаковы.
Фигуры, изображенные на рисунке 4а,б,в – это разные представления одного и того же графа. Согласитесь, увидеть это не так-то просто!
Рис.4,а Рис.4,б Рис.4,в
На рисунках 5 а,б,в,г изображены четыре графа . Граф (Рис.5,а) является исходным, остальные три (Рис5б,в,г) – его подграфы. Это означает, что в них были выбраны лишь некоторые ребра и вершины исходного графа. Подграфы позволяют изучить графы по частям.
Рис.5,а Рис.5,б
Рис.5,в Рис.5,г
Обычно различают три типа графов: обыкновенные графы, мультиграфы и псевдографы. На рисунках 6,а,б,в представлены все три типа графов. 
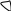
Рис.6,а Рис.6,б Рис.6,в