Задача 1. По первой группе предприятий 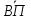= =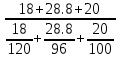 = 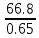102.7%По второй группе 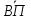= = 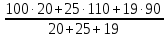= 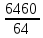100,9%По двум группам 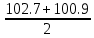= 101.8%По двум группам предприятий план перевыполняется.Задача 2. Второй год по сравнению с первымТовар А.- цена снизилась на 38.5% (100 – 61.5)- прирост физического объема составил 13.6% (113.6 – 100)i_pq=0.615*1.136=0.699 ,т.е. стоимость товарооборота снизилась на 30.1% (100 – 69.9)Товар В.i_pq=0.917*0.87=0.797 (себестоимости)(физического объема)(объем в ценах)Третий год по сравнению со вторым.Товар А.Это означает, что цена возросла на 87.5% (187.5 – 100). Прирост физического объема составил 16% (116 – 100). i_pq=1.875*1.16=2.175Товар В.i_pq=0.809*1.05=0.85 I = Iq · Iz = 1.063 · 0.949 = 1.009 По товару А произошло снижение цены при увеличении кол-ва продукции, при этом товарооборот снизился. По продукции В цена увеличилась почти в два раза, товарооборот за счет этого увеличился более чем в два раза.Задача 3.

	кредиторская	дебиторская
Промышленность	49,18	39,1
Сельское хозяйство	10,44	1,53
Строительство	7,98	7,14
Транспорт	11,05	7,97
Связь	0,25	1,63
Торговля	7,33	25,63
Оптовая торговля	0,79	3,75
ЖКХ	10,01	5,13
Другие отрасли	2,96	8,12
Итого	100	100

---

Промышленность = 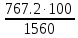= 49,18%(кредиторская)Остальные считаем аналогично.Больше всего кредиторской и дебиторской задолженности в промышленной области, меньшая часть в связи. Задача 4.Заданный планом прирост выпуска продукции (18%) выражаем в форме коэффициента роста выпуска продукции в 2019 г. по сравнению с 2018 г.:1 + 0,18 = 1,18.Фактический процент роста выпуска продукции (113,4%) выражаем в форме коэффициента:112,3 / 100 = 1,123ОВВП(%) = Задача 5.Абсолютный приростцепной прирост: ∆y_ц = y_i - y_i-1базисный прирост: ∆y_б = y_i - y₁Темп приростацепной темп прироста: T_прцi = ∆y_i / y_i-1базисный темп прироста: T_пpб = ∆y_бi / y₁Темп ростацепной темп роста: T_pцi = y_i / y_i-1базисный темп роста: T_pб = y_бi / y₁Абсолютное значение 1% приростацепной: 1%_цi = y_i-1 / 100% базисный: 1%_б = y_б / 100%

Период	ожидаемая продолжительность жизни, лет	Абсолютный прирост	Темп прироста, %	Темпы роста, %	Абсолютное содержание 1% прироста	Темп наращения, %
2009	68.78	-	-	100	-	0
2010	68.94	0.16	0.23	100.23	0.6878	0.23
2011	69.83	0.89	1.29	101.29	0.6894	1.29
2012	70.24	0.41	0.59	100.59	0.6983	0.6
2013	70.76	0.52000000000001	0.74	100.74	0.7024	0.76
2014	70.93	0.17	0.24	100.24	0.7076	0.25
2015	71.39	0.45999999999999	0.65	100.65	0.7093	0.67
2016	71.87	0.48	0.67	100.67	0.7139	0.7
2017	72.7	0.83	1.15	101.15	0.7187	1.21
2018	72.91	0.20999999999999	0.29	100.29	0.727	0.31
Итого	708.35

---

Год	лет	Абсолютный прирост		Темп роста		Темп прироста		Абсолютное содержание 1% прироста
		цепной	базисный	цепной	базисный	цепной	базисный
2009	68.78	-	-	100	100	-	-	-
2010	68.94	0.16	0.16	100.23	100.23	0.23	0.23	0.6878
2011	69.83	0.89	1.05	101.29	101.53	1.29	1.53	0.6894
2012	70.24	0.41	1.46	100.59	102.12	0.59	2.12	0.6983
2013	70.76	0.52	1.98	100.74	102.88	0.74	2.88	0.7024
2014	70.93	0.17	2.15	100.24	103.13	0.24	3.13	0.7076
2015	71.39	0.459	2.61	100.65	103.79	0.65	3.79	0.7093
2016	71.87	0.48	3.09	100.67	104.49	0.67	4.49	0.7139
2017	72.7	0.83	3.92	101.15	105.7	1.15	5.7	0.7187
2018	72.91	0.209	4.13	100.29	106	0.29	6	0.727

Среднее значение ожидаемая продолжительность жизни с 2009 по 2018 составило 70.84 лет

---

Средний темп роста Средний абсолютный прирост. С каждым годом продолжительность жизни увеличивалась на 0.46 лет Задача 6.Находим параметры уравнения методом наименьших квадратов. Система уравнений МНК: an + b∑t + c∑t² = ∑y a∑t + b∑t² + c∑t³ = ∑yt a∑t² + b∑t³ + c∑t⁴ = ∑yt²

t	y	t2	y2	t y	t3	t4	t2 y
84	2	7056	4	168	592704	49787136	14112
95	2.3	9025	5.29	218.5	857375	81450625	20757.5
91	1.5	8281	2.25	136.5	753571	68574961	12421.5
110	2.8	12100	7.84	308	1331000	146410000	33880
121	4.2	14641	17.64	508.2	1771561	214358881	61492.2
161	2.6	25921	6.76	418.6	4173281	671898241	67394.6
166	2.2	27556	4.84	365.2	4574296	759333136	60623.2
171	3.5	29241	12.25	598.5	5000211	855036081	102343.5
175	8.5	30625	72.25	1487.5	5359375	937890625	260312.5
174	4.2	30276	17.64	730.8	5268024	916636176	127159.2
186	4.6	34596	21.16	855.6	6434856	1196883216	159141.6
210	3.9	44100	15.21	819	9261000	1944810000	171990
251	6.5	63001	42.25	1631.5	15813251	3969126001	409506.5
1995	48.8	336419	229.38	8245.9	61190505	11812195079	1501134.3
153.462	3.754	25878.385	17.645	634.3

---

Для наших данных система уравнений имеет вид 13a + 1995b + 336419c = 48.8 1995a + 336419b + 61190505c = 8245.9 336419a + 61190505b + 11812195079c = 1501134.3 Получаем c = -1.1E-5, b = 0.0285, a = -0.335 Уравнение тренда: y = -1.1E-5t²+0.0285t-0.335 Ошибка аппроксимации в пределах 5%-7% свидетельствует о хорошем подборе уравнения тренда к исходным данным. Эмпирическое корреляционное отношение вычисляется для всех форм связи и служит для измерение тесноты зависимости. Изменяется в пределах [0;1]. = Задача 7.Рассчитаем среднее время обработки одной детали в выборочной совокупности. Все расчёты оформим в таблицу.

Группы	Середина интервала, xцентр	Кол-во, fi	xi·fi	Накопленная частота, S	|x-xср|·fi	(x-xср)2·fi
18 - 20	19	2	38	2	10.96	60.061
20 - 22	21	8	168	10	27.84	96.883
22 - 24	23	24	552	34	35.52	52.57
24 - 26	25	50	1250	84	26	13.52
26 - 28	27	12	324	96	30.24	76.205
28 - 30	29	4	116	100	18.08	81.722
Итого		100	2448		148.64	380.96

мин.Дисперсия выборочной совокупности Средняя ошибка выборки составит = 0.185С вероятностью 0,997 рассчитаем предельную ошибку выборочной  средней.Δ = μ * tt - коэффициент доверия (равен 3)Δ = 0.185 * 3 = 0.555 мин.

---

Смотрите также файлы

• Внеурочное мероприятие по литературе для 7 класса Литературная шкатулка.doc

• Кыргыз Республикасынын иимнин Ички коопсуздуктун аскерлер кызматынын офицердик курамы чн буюм млкн чыгымдоонун жана жабдуунун.docx

• Гнойносептические заболевания в акушерстве. Септический шок.pdf

• Синдром пневмоторакса.docx

• Сынып 7.docx