Контрольная работа

по дисциплине: «Управление рисками и страхование»

Вариант – 9

1. Статистические методы оценки рисков

В таблице 1 представлены данные по объемам реализации компании. Рассчитайте вероятность каждого значения временного ряда, а также следующие показатели его динамики:

- размах вариации

- математическое ожидание

- дисперсия

- среднеквадратическое отклонение

- коэффициент вариации

Таблица 1 – Данные по объемам реализации компании в стоимостном выражении

Месяц	янв	фев	мар	апр	май	июн	июл	авг	сен	окт
Объем реализации, тыс. у. е.	150	170	162	150	168	200	162	170	206	168

Решение:

1) Размах вариации рассчитаем по формуле: R = X_max - X_min

R = 206 – 150 = 56

Таким образом, за указанный период разница между минимальным и максимальным значением объема реализации составила 56 тыс. у. е. Но этот показатель дает очень грубую оценку риску, так как он является абсолютным показателем и зависит только от крайних значений ряда.

2) Математическое ожидание определим по формуле: M(E) = ∑(Х_k× Р_k) Для расчета вероятности каждого значения выпишем все значения ряда без повторений. Для удобства расчетов составим таблицу (см. таблицу 2). Рассчитаем вероятность каждого значения ряда по формуле: Рk = k : N Полученные результаты занесем в строку 1 таблицы 2. Найдем произведение каждого значения и его вероятности. Результаты занесем в строку 2 таблицы 2. Сумма полученных произведений является значением математического ожидания данного временного ряда: M(E) = 170,6. Математическое ожидание показывает наиболее правдоподобное значение объема реализации в месяц за указанный период.

---

3) Дисперсия временного ряда - мера разброса значений случайной величины относительно её математического ожидания и определяется по формуле: σ² (Ε) = ∑[( Х_k – M(E))² × Р_k].

Рассчитаем значение дисперсии поэтапно. Сначала найдем отклонение каждого значения ряда от среднего ожидаемого значения (строка 3 таблицы 2). Затем возведем в квадрат полученные значения отклонений (строка 4 таблицы 2). Наконец, умножим значения строки 4 на соответствующие значения вероятности (строка 5 таблицы 2). Сумма значений строки 5 представляет собой значение дисперсии данного временного ряда:

σ² (Ε) = 312,84

Использование дисперсии как меры риска не всегда удобно, так как. размерность ее равна квадрату единицы измерения случайной величины.

Таблица 2 – Расчет статистических показателей

№ п/п	Показатели	Значения (ХК)						Итого
		150	170	162	168	200	206
1	2	3	4	5	6	7	8	9
1	Вероятность (Рк)	2:10 = 0,2	2:10 = 0,2	2:10 = 0,2	2:10 = 0,2	1:10 = 0,1	1:10 = 0,1	1
2	Математическое ожидание М(Е) = ∑(Хk× Рk)	150×0,2 = 30	170×0,2 = 34	162×0,2 = 32,4	168×0,2 = 33,6	200×0,1 = 20	206×0,1 = 20,6	170,6
3	Хk – M(E)	150 – 170,6 = -20,6	170-170,6 = -0,6	162-170,6 = -8,6	168-170,6 = -2,6	200–170,6 = 29,4	206-170,6 = 35,4	-
4	(Хk – M(E))2	424,36	0,36	73,96	6,76	864,36	1253,16	-
5	Дисперсия σ2 (Ε) = ∑[(Хk – M(E))2 × Рk)]	424,36×0,2 = 84,872	0,36×0,2 = 0,072	73,96×0,2 = 14,792	6,76×0,2 = 1,352	864,36× 0,1 = 86,436	1253,16× 0,1 = 125,316	312,84
6	Стандартное (среднеквадратическое) отклонение σ(Ε) = Ѵ¯σ2 (Ε)	-	-	-	-	-	-	17,69
7	Коэффициент вариации Kv = σ(Ε) : M(E)	-	-	-	-	-	-	0,1037 (10,37%)

---

4) Стандартное (среднеквадратическое) отклонение определим по формуле: σ(Ε) = Ѵ¯σ² (Ε).

σ(Ε) = 17,69.

Таким образом, значение объема реализации за указанный период в среднем изменяется на 17,69 тыс. у. е. в месяц.

5) Коэффициент вариации, выраженный в процентах, показывает, насколько велики были отклонения параметров за анализируемый период. Рассчитаем значение коэффициента вариации по формуле: K_v = σ(Ε) : M(E)

K_v = 17,69:170,6 = 0,1037 (т.е. 10,37 %).

Вывод: Таким образом, значение объема реализации за указанный период изменяется в среднем на 10,37%. Совокупность стабильна, так как коэффициент вариации меньше 30% (≤ 0,3).
2. Метод учета риска
при расчете чистой приведенной стоимости NPV
Первоначальные инвестиции компании в реализацию проекта составили 3 000 у. е.

Безрисковая дисконтная ставка составляет 8 %.

Плата за риск – 2 %.

Динамика чистых денежных потоков представлена в таблице 3.

Рассчитайте эффективность проекта с учетом и без учета риска. Опишите недостатки данного метода учета рисков.

Таблица 3 - Динамика чистых денежных потоков

Год	1	2	3	4	5
Стоимость денежного потока, у. е.	-5 000	-1 000	2 000	4 000	7 000

Решение:

Для удобства расчетов составим таблицу 4. Рассмотрим в таблице динамику денежных потоков по годам.

Таблица 4 - Расчет чистой приведенной стоимости NPV проекта
с учетом и без учета риска

№ п/п	Показатели	Годы							Сумма, тыс. у.е.
		0	1	2	3	4	5
1	2	3	4	5	6	7	8	9
1	Первоначальные инвестиции (I0), тыс. у. е.	3000
2	Безрисковая годовая ставка дисконта rt', %		8	8	8	8	8
3	Премия за риск rt*, %		2	2	2	2	2
4	Годовая ставка дисконта с учетом премии за риск rt' +rt*, %		10	10	10	10	10
5	Чистые денежные потоки (CFt), тыс. у. е.		-5 000	-1 000	2 000	4 000	7 000
6	Приведенная стоимость чистых денежных потоков (без учета риска) PVt', тыс. у. е		-5000:1,08 = −4 629,63	-1000: 1,082= −857,34	2000: 1,083= 1 587,68	4000: 1,084= 2 940,1	7000: 1,085= 4 764,1	3 904,91
7	Приведенная стоимость чистых денежных потоков (с учетом риска) PVt*, тыс. у. е.		-5 000:1,1 = −4 545,45	-1 000:1,12 = −826,45	2 000:1,13 = 1 502,63	4 000:1,14 = 2 732,05	7 000:1,15 = 4 241,14	3 103,92
8	Чистая приведенная стоимость (NPV') без учета риска, тыс. у. е	904,91
9	Чистая приведенная стоимость (NPV*) с учетом риска, тыс. у. е.	103,92

---

3. Метод построения «дерева решений»

Международная нефтяная компания должна принять решение о бурении скважины.

В начальный момент времени t=0 необходимо потратить $ 9 млн на проведение трехмерной сейсмической разведки, которая увеличивает шансы успешной разработки. Вероятность положительных результатов разведки составляет 90 %, отрицательных – 10 %.

Если в результате разведки будет выяснено, что потенциал скважины достаточно высок, то компания инвестирует еще $ 15 млн на бурение (t=1).

Вероятность того, что скважина все-таки окажется сухой составляет 20 %. В случае открытия месторождения компания сможет получать прибыль около $ 50 млн в год при оптимистическом сценарии (вероятность 10 %), $ 35 млн – при наиболее вероятном развитии событий (вероятность 80 %) и $ 10 млн – при наихудшем сценарии (вероятность 10 %).

Срок добычи нефти в случае открытия месторождения составляет 3 года.

Ставка цены капитала компании при реализации данного проекта составляет 10 %.

Постройте дерево решений, рассчитайте финансовый результат каждого варианта и определите целесообразность реализации проекта.
Решение:



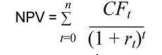
Построим древо решений (рисунок 1).



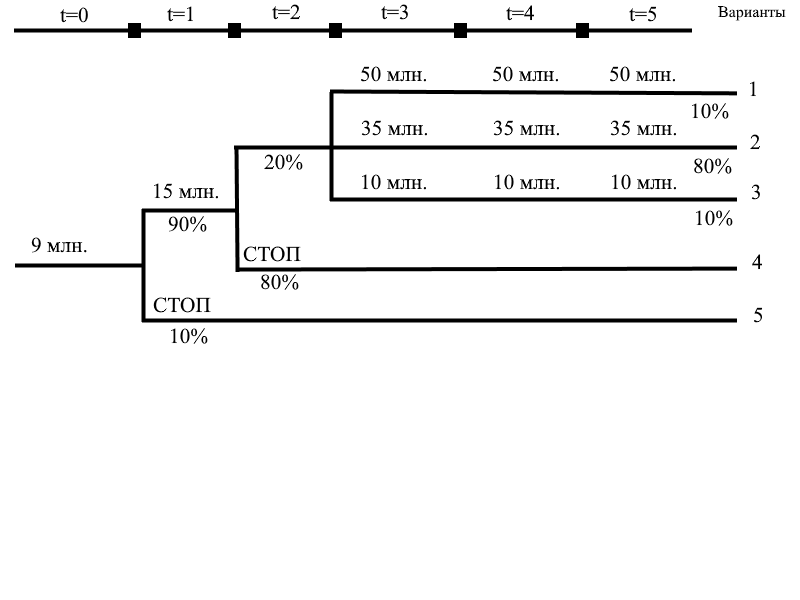
Рисунок 1 – Дерево решений

Данные занесем в таблицу 5. Затем найдем «совместную» вероятность каждого из вариантов. Согласно представленному рисунку, вероятность составит:

р₁ = 0,9 × 0,2 × 0,1 = 0,018;

р₂ = 0,9 × 0,2 × 0,8 = 0,144;

р₃ = 0,9 × 0,2 × 0,1 = 0,018;

Имея значения доходности различных вариантов развития инвестиционного проекта и вероятностное распределение этих значений, можно рассчитать математическое ожидание доходности проекта (среднее ожидаемое значение).

Таблица 5 – Расчет совокупной эффективности проекта

---

Показатели	Годы						NPV	P		NPV×P
	0	1	2	3	4	5
1	2	3	4	5	6	7	8	9		10
Годовая ставка дисконта rt		0,1	0,1	0,1	0,1	0,1
Чистый поток средств CFt1	-9 000 000	-15 000 000		50 000 000	50 000 000	50 000 000
Приведенная стоимость чистых денежных потоков PVt1	-9 000 000	-13 636 363,6	0,0	37 565 740,1	34 150 672,8	31 046 258,9	80 126 308,2	0,9 × 0,2 × 0,1 = 0,018		1 442 273,55
Чистый поток средств CFt2	-9 000 000	-15 000 000		35 000 000	35 000 000	35 000 000
Приведенная стоимость чистых денежных потоков PVt2	-9 000 000	-13 636 363,6	0,0	26 296 018,03	23 905 470,94	21 732 381,25	49 297 506,62	0,9 × 0,2 × 0,8 = 0,144		7 098 840,95
Чистый поток средств CFt3	-9 000 000	-15 000 000		10 000 000	10 000 000	10 000 000
Приведенная стоимость чистых денежных потоков PVt3	-9 000 000	-13 636 363,6	0,0	7 513 148	6 830 134,6	6 209 251,8	-2 083 829,2	0,9 × 0,2 × 0,1 = 0,018		-37 508,9
Чистый поток средств CFt4	-9 000 000	-15 000 000
Приведенная стоимость чистых денежных потоков PVt4	-9 000 000	-13 636 363,6	0,0	0,0	0,0	0,0	-22 636 363,6	0,9 × 0,8 = 0,72		-16 298 181,79
Чистый поток средств CFt5	-9 000 000
Приведенная стоимость чистых денежных потоков PVt5	-9 000 000	0,0	0,0	0,0	0,0	0,0	-9 000 000	0,1		-900 000
Ожидаемое значение доходности инвестиционного проекта									-8 694 576,19

---

Смотрите также файлы

• пр. зад. 3.docx

• Типология государств.docx

• Дисциплина Основы предпринимательской деятельности.docx

• Общая характеристика речевых нарушений. 4.doc

• Философия ее предмет и круг проблемм.docx