ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 41
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования
Балтийский государственный технический университет
«ВОЕНМЕХ» им. Д.Ф. Устинова
Кафедра

ДисциплинааМатематика
Индивидуальное Домашнее задание № __19.1__
__________________________________________________________
__________________________________________________________
_________________________________________________________
| Выполнили студенты | Чудов.С Львов.И | |||
| Фамилия И.О. | ||||
| группа | А411С _________________ | | ||
| | ||||
| Преподаватель | Еськова.Е.А | |||
| | Фамилия И. О. | |||
| | Подпись преподавателя | Дата | ||
| Допуск | | | ||
| Выполнение | | | ||
| | | | ||
Санкт-Петербург
2023 г.
В результате эксперимента получены данные, записанные в виде статистического ряда.
Требуется:
а) записать значения результатов эксперимента в виде вариационного ряда
;
б) найти размах варьирования и разбить его на 9 интервалов;
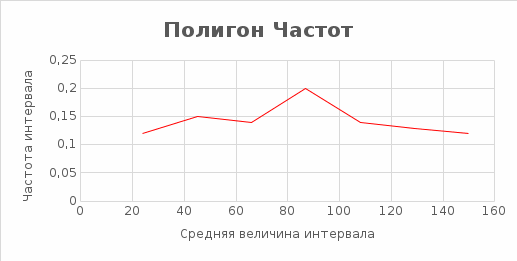
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
г) Найти числовые характеристики выборки
д) принять в качестве нулевой гипотезу Н0: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение, проверить её, пользуясь критерием Пирсона при уровне значимости
е) найти доверительные интервалы для математического ожидания и среднего квадратичного отклонения при степени надёжности
а) записать значения результатов эксперимента в виде вариационного ряда;
Таблица 1.
| 15 | 16 | 17 | 17 | 18 | 19 | 21 | 25 | 30 | 32 |
| 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 | 41 | 48 |
| 49 | 50 | 51 | 52 | 53 | 54 | 55 | 56 | 57 | 61 |
| 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 72 | 73 |
| 76 | 77 | 78 | 80 | 81 | 82 | 84 | 85 | 86 | 87 |
| 88 | 89 | 90 | 91 | 92 | 93 | 93 | 94 | 94 | 96 |
| 97 | 98 | 99 | 100 | 101 | 102 | 103 | 104 | 105 | 109 |
| 110 | 112 | 113 | 114 | 115 | 121 | 123 | 124 | 125 | 126 |
| 128 | 129 | 130 | 131 | 135 | 137 | 138 | 139 | 140 | 141 |
| 142 | 144 | 145 | 146 | 147 | 149 | 150 | 151 | 158 | 159 |
б) Находим размах варьирования
| w=144 |
| |
| h=144:7=21 |
В качестве границы первого интервала возьмём X(min). Границы следующих интервалов вычисляем по формуле:
Находим середины интервалов:
Таблица 2.
| Номер частичного интервала | Границы интервала | Середина интервала | Частота интервала | Относительная частота | Плотность относительной частоты | |
| 1 | 13,5 | 34,5 | 24 | 12 | 0,12 | 0,0057 |
| 2 | 34,5 | 55,5 | 45 | 15 | 0,15 | 0,0071 |
| 3 | 55,5 | 76,5 | 66 | 14 | 0,14 | 0,0067 |
| 4 | 76,5 | 97,5 | 87 | 20 | 0,2 | 0,0095 |
| 5 | 97,5 | 118,5 | 108 | 14 | 0,14 | 0,0067 |
| 6 | 118,5 | 139,5 | 129 | 13 | 0,13 | 0,0062 |
| 7 | 139,5 | 160,5 | 150 | 12 | 0,12 | 0,0057 |
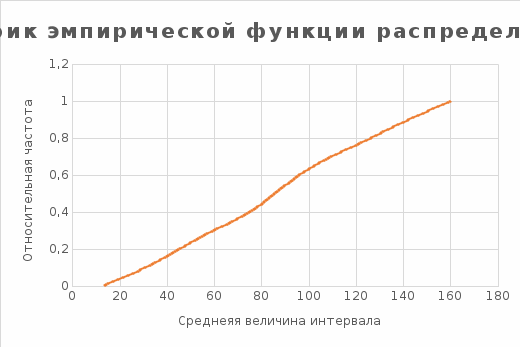
в) построить полигон частот, гистограмму относительных частот и график эмпирической функции распределения;
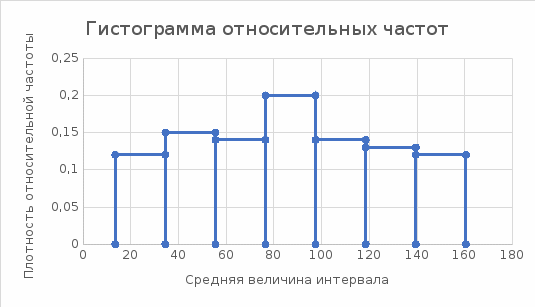
Таблица 3.
| F(13,5) | 0 |
| F(34,5) | 0,12 |
| F(55,5) | 0,27 |
| F(76,5) | 0,41 |
| F(97,5) | 0,61 |
| F(118,5) | 0,75 |
| F(139,5) | 0,88 |
| F(160,5) | 1 |
г) Найдём выборочное среднее
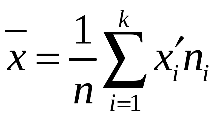 и выборочную дисперсию
и выборочную дисперсию 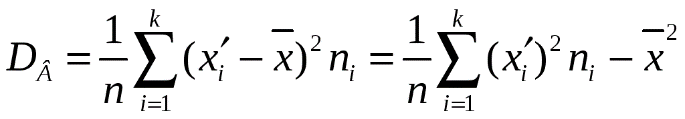
Составляем расчётную таблицу:
Таблица 4.
| m | Граница интервала x | Частота интервала, n | n*x' | (x')^2 | n*(x')^2 | Середина интервала,x' | |
| 1 | 13,5 | 34,5 | 12 | 288 | 576 | 6912 | 24 |
| 2 | 34,5 | 55,5 | 15 | 675 | 2025 | 30375 | 45 |
| 3 | 55,5 | 76,5 | 14 | 924 | 4356 | 60984 | 66 |
| 4 | 76,5 | 97,5 | 20 | 1740 | 7569 | 151380 | 87 |
| 5 | 97,5 | 118,5 | 14 | 1512 | 11664 | 163296 | 108 |
| 6 | 118,5 | 139,5 | 13 | 1677 | 16641 | 216333 | 129 |
| 7 | 139,5 | 160,5 | 12 | 1800 | 22500 | 270000 | 150 |
| ∑ | | | 100 | 8616 | |  xср = 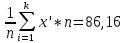 899280 | |
Таблица 5.
| Выборочное среднее xср | |||||
| | | | | ||
| | | |
| ||
| Выборочная дисперсия Dв | | ||||
| | | | | ||
| | | |  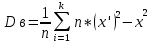 =1569,254 =1569,254 | ||
| Выб. ср. квадр. Откл. σв |  σв = 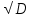 в=39,61382 в=39,61382 | ||||
| | | | | ||
| | | | | ||
| Несмещенная оценка σв2 | σв2 = √Dв2=39,81338 | ||||
| | | | | ||
| | | |  Dв2 =(n/(n-1)) * Dв=1585,105 | ||
| Смещенная оценка Dв2 | | ||||
д) Согласно критерию Пирсона необходимо сравнить эмпирические и теоретические частоты. Эмпирические частоты даны. Найдём теоретические частоты. Для этого пронумеруем Х, т.е. перейдём к случайной величине