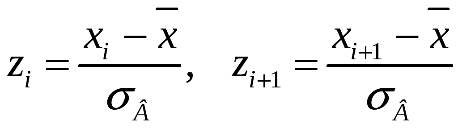и вычислим концы интервалов: , причём наименьшее значение , точнее положим стремящимся к , а наибольшее, точнее - стремящемся к .

Таблица 6.

i	Границы интервала Xi; Xi+1			Xi-Xср	Xi+1-Xср	Границы интервала Zi; Zi+1
	Xi	Xi+1				Zi = (Xi-Xср) / σв	Zi+1 = (Xi+1-Xср) / σв
1	13,5	34,5		-72,66	-51,66	-	-1,30409
2	34,5	55,5		-51,66	-30,66	-1,30409	-0,77397
3	55,5	76,5		-30,66	-9,66	-0,77397	-0,24385
4	76,5	97,5		-9,66	11,34	-0,24385	0,286264
5	97,5	118,5		11,34	32,34	0,286264	0,816382
6	118,5	139,5		32,34	53,34	0,816382	1,3465
7	139,5	160,5		53,34	74,34	1,3465	-

---

Таблица 7.

i	Границы интервала Xi; Xi+1				Ф(Zi )		Ф(Zi+1 )		Pi = Ф(Zi+1 ) - Ф(Zi )				n'I = 100Pi
	Zi	Zi+1
1	-	-1,30409		-0,5		-0,4039		0,096101				9,610137
2	-1,30409	-0,77397		-0,4039		-0,28053		0,123372				12,33722
3	-0,77397	-0,24385		-0,28053		-0,09633		0,184198				18,41983
4	-0,24385	0,286264		-0,09633		0,112662		0,20899				20,89901
5	0,286264	0,816382		0,112662		0,292859		0,180197				18,01972
6	0,816382	1,3465		0,292859		0,410929		0,11807				11,80702
7	1,3465	-		0,410929		0,5		0,089071				8,907067
Сумма								1				100

---

Таблица 8.

i	ni	n'i	ni-n'i		(ni-n'i)^2		(ni-n'i)^2/n'i	ni^2	ni^2/n'i
1	12	9,610137	2,389863		5,711446		0,594315	144	14,98418
2	15	12,33722	2,662781		7,090403		0,574716	225	18,2375
3	14	18,41983	-4,41983		19,53487		1,060535	196	10,64071
4	20	20,89901	-0,89901		0,808223		0,038673	400	19,13966
5	14	18,01972	-4,01972		16,15812		0,896691	196	10,87697
6	13	11,80702	1,192978		1,423197		0,120538	169	14,31352
7	12	8,907067	3,092933		9,566233		1,074005	144	16,16694
∑	100	100	-		-		4,359	-	104,3595
X^2набл =	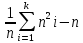			4,359
Контроль: ∑n^2i/n'I - n				4,359
Число степени свободы k:				4
X^2кр =				13,3
Так как X^2набл < X^2кр, то гипотеза H0 о нормальном распределении генеральной совокупности принимается

---

Таблица 9.

Доверительный интервал :(Хср - (σв2/√n)*ty; Хср + (σв2/√n)*ty)

(78,2610; 94,0589)

Доверительный интервал, покрывающий среднее квадратичное отклонение σ, где q = 0,143: (σв2(1-q);σв2(1+q))

(34,12; 45,506)

34,12

---

Смотрите также файлы

• Возрастная анатомия, физиология и гигиена.docx

• Числовые и буквенные выражения. Формулы.docx

• Конкурс Цветами улыбается весна.docx

• Проектный облик перспективного малого космического аппарата с маршевой электроракетной двигательной установкой Власенков Е. В. 1.pdf

• Профессиональный стандарт педагога.docx