Структурная схема, соответствующая этому выражению, приведена на рис. 3.28.



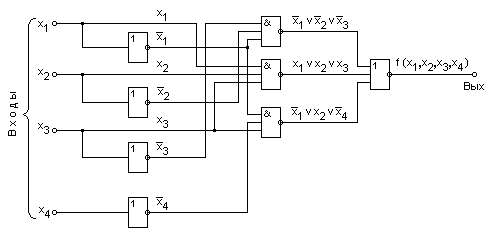
рис 3.28



Переход от сокращенной формы (3.15) к МДНФ (3.16) был осуществлен путем исключения лишних имплнкант и . Покажем допустимость подобного исключения членов из логического выражения.

Импликанты и обращаются в единицу соответственно при следующих наборах значений аргументов:

x₁ = 0; х₂ = 0; х₃ = 0 и х₂ = 1; х₃ = 1; х₄ = 0 (3.17)

Роль этих имликант в выражении сокращенной формы функции (3.15) заключается лишь в том, чтобы на приведенных наборах (3.17) значений аргументов присваивать функции значение 1. Однако при этих наборах функция имеет значение 1 из-за остальных импликант выражения (3.15). Действительно, подставляя значения (3.17) в (3.16), получаем:

при x₁ = 0, x₂ = 0, x₃ = 0





 

при х₂ = 1; х₃ = 1; х₄ = 0



Таким образом, доказана справедливость операции исключения из выражения (3.15) членов и .

До сих пор рассматривалось получение минимальной ДНФ. При использовании метода Квайна для получения минимальной конъюнктивной нормальной формы (МК.НФ) логической функции имеются следущие особенности:

исходной для минимизации формой логического выражения заданной функции является СКНФ;

пары склеиваемых членов имеют вид и ;

---

операция поглощения проводится в соответствии с выражением

Рассмотрим применение метода Квайна на примере минимизации функции, заданной таблицей истинности (табл. 3.8).

Совершенная КНФ рассматриваемой функции

Склеивающиеся пары членов:

первый и третий члены (результат склеивания );

первый и четвертый члены (результат склеивания ):

второй и третий члены (результат склеивания ).

Таблица 3.8
x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f(x1,x2,x3)	1	0	0	0	1	0	1	1

 

Таблица 3.9
Простые импликанты	Члены СДНФ
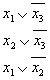	X		X
	X			X
		X	X

---

 

Проводя операции склеивания и поглощения, получаем

Члены операции склеивания



Полученное выражение явлиется сокращенной формой функции. Для перехода к минимальной форме строим иммлнк.шгную матрицу (табл. 3.9).



Все столбцы матрицы перекрываются импликантами и . Следовательно, член является лишним и минимальная конъюнктивная нормальная форма (МКНФ) заданной функции

---

Минимизация логических функций методом карт Вейча

Метод Квайна имеет четко сформулированные правила проведения отдельных операций, благодаря чему он может быть использован для минимизации функций с использованием ЭВМ в тех случаях, когда минимизируемая функция достаточно сложна (содержит большое число аргументов и каноническая форма имеет большое число членов). Однако для минимизации функции ручным способом (без использования ЭВМ) этот метод оказывается весьма трудоемким. Трудоемкость метода Квайна связана с необходимостью попарного сравнения всех членов выражения для выявления склеиваемых членов.

Метод минимизации функции с помощью карт Вейча обеспечивает простоту получения результата. Он используется пои минимизации относительно несложных функций (с числом аргументов до 5) ручным способом. В отличие от метода Квайна этот метод требует элементов изобретательности и не может быть использован для решения задачи минимизации с помощью ЭВМ. Карга Вейча прдставляет собой определенную форму таблицы истинности. Табл. 3.10 являются картами Вейча для функций соответственно двух (а), трех (б), четырех (в) аргументов.

Каждая клетка карты соответствует определенному набору значений аргументов. Этот набор аргументов определяется присвоением значения лог. 1 буквам, на пересечении строк и столбцов которых расположена клетка. Так, в карте функций четырех аргументов (табл. 3.10,в) клегки первой строки соответствуют следующим комбинациям аргументов:

• 
  первая клетка
  
• 
  вторая клетка
  
• 
  третья клетка
  
• 
  четвертая клетка
  

Число клеток карты равно числу всех возможных наборов значений аргументов 2ⁿ (n – число аргументов функций). В каждую из клеток карты записывается значение функции на соответствующем этой клетке наборе значений аргументов. Пусть функция задана таблицей истинности в форме, которая использовалась ранее (табл. 3.11). Таблица истинности этой функции в форме карты Вейча представлена табл. 3.12.

Как видим, карта Вейча определяет значения функции на всех возможных наборах значений аргументов и, таким образом, является таблицей истинности. Карты Вейча компактны, но главное их достоинство состоит в следующем. При всяком переходе из одной клетки в соседнюю вдоль столбца или строки изменяется значение лишь одного аргумента функции. Следовательно, если в паре соседних клеток содержится 1, то над соответствующими им членами канонической формы может быть проведена операция склеивания. Таким образом, облегчается поиск склеиваемых членов.

---

Таблица 3.12
x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f(x1,x2,x3)	0	1	0	1	0	0	1	1

Сформулируем правила получения МДНФ функций с помощью карт Вейча.

Все клетки, содержащие 1, объединяются в замкнутые области. При этом каждая область должна представлять собой прямоугольник с числом клеток 2^k, где k = 0, 1, 2, ... Таким образом, допустимое число клеток в области – 1, 2, 4, 8,... Области могут пересекаться и одни и те же клетки могут входить в разные области.

Затем проводится запись выражения МДНФ функции. Каждая из областей в МДНФ представляется членом, число букв в котором на k меньше общего числа аргументов функции n (т. е. равно n – k). Каждый член МДНФ составляется лишь из тех аргументов, которые для клеток соответствующей области имеют одинаковое значение (без инверсии либо с инверсией).

Таким образом, при охвате клеток замкнутыми областями следует стремиться, чтобы число областей было минимальным (при этом минимальным будет число членов в МДНФ функции), а каждая область содержала возможно большее число клеток (при этом минимальным будет число букв в членах МДНФ функции).

---

Смотрите также файлы

• Лекции, напишите эссе Условия профессионального развития личности.docx

• Задача по теме 13 раздела 2 Совершенная конкуренция объем выпуска.docx

• Интерпретация художественного текста. Вопрос 1.doc

• Доклад по дисциплине избранные главы биоорганической химии.docx

• управление персоналом 3.docx