Синтез логических устройств с несколькими выходами

Пусть синтезируемое логическое устройство имеет п входов и т выходов (рис. 3.30). На каждом из выходов должна быть сформирована определенная функция входных переменных.

Эта задача могла бы быть решена синтезированием раздельно действующих узлов, каждый из которых реализовывал бы определенную выходную функцию. Однако, если даже каждый из этих узлов будет построен минимальным образом, в целом логическое устройство может оказаться не минимальным. Действительно, такое устройство могло бы быть подвергнуто минимизации путем использования общих элементов и нескольких устройствах, реализующих различные выходные функции.

Из этих соображений принеленне каждой из выходных функций к минимальной форме не является услонисм получения минимального в целом устройства. При минимизации устройств и целим некоторые нз функций могут оказаться представленными и неминимальной форме.

Принцип получения минимальной формы устройства сводится к нахождению минимального набора членов с минимальным числом входящих в них букв, достаточного для получения всех формируемых устройством функций.

Метод построения минимальных логических устройств с несколькими выходами рассмотрим на примере реализации устройства, способ функционирования которого задан табл. 3.23.

Записываем наборы аргументов, на которых хотя бы одна из выходных функций имеет значение 1, Рядом в таблице в качестве признака записываем функции, принимающие значения 1 при данном наборе аргументов (табл. 3.24).



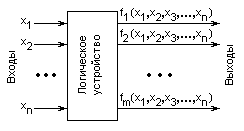
рис 3.24

Затем проводим операцию склеивания и получающиеся при этом члены заносим в табл. 3.25, рядом с членами записываем признаки в виде функций

---

, общих в признаках той пары членов табл. 3.24, склеиванием которых они получены. Так склеивание членов табл. 3.24 и

Приводит в табл. 3.25 к члену ; склеивание членов

и приводит к и т. д.

Таблица 3.23
X1	0	0	0	0	1	1	1	1
X2	0	0	1	1	0	0	1	1
X3	0	1	0	1	0	1	0	1
f1(x1,x2,x3)	0	1	0	1	0	0	1	1
f2(x1,x2,x3)	0	0	1	0	1	1	0	0
f2(x1,x2,x3)	0	1	1	1	1	1	0	0

---

 

 

Таблица 3.25
	f1f3
	f3
	f3
	f1
	f2f3
	f1

Не проводится операция склеивания над членами, в признаках которых не имеется общих функций.

Далее проводится операция поглощения членами табл. 3.25 членов табл. 3.24. Операция поглощения может проводиться лишь над членами, имеющими одинаковую комбинацию функций в признаках.

Указанные операции склеивания и поглощения повторяются, пока их проведение оказывается возможным. Затем составляется импликантная таблица (табл. 3.26). Определяется набор импликант, обеспечивающий перекрятие всех столбцов импликантной таблицы. Этот набор импликант приведен в табл. 3.27.

Записываем логические выражения для выходных функций, составленные из этих импликант, в признаках которых содержатся заданные функции:



 

 

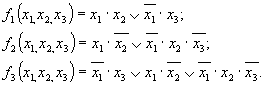
Таблица 3.26

f1

f3

f2

f3

f1

f3

f2

f3

f2

f3

f1

f1

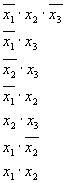(f2f3)

X

X

(f1f3)

X

X

X

X

(f3)

X

X

(f3)

X

X

(f1)

X

(f2f3)

X

X

X

X

(f1)

X

X

---

 



Легко убедиться, что выражение для функции не является минимальным. Минимальная для этой функции форма





Однако замена в выражении функции f₃ члена членом

невыгодна, так как член присутствует и в выражении f₂ и он должен быть сформирован для этой функции.

На рис. 3.31 приведена функциональная схема устройства, обеспечивающего заданное табл. 3.23 функционирование. Как нидно из схемы, ряд элементов участвует одновременно в формировании нескольких выходных функций.



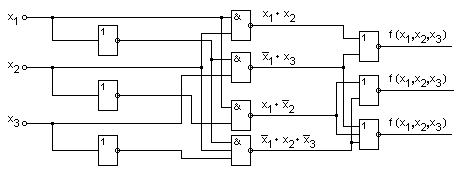
рис 3.31

---

Синтез логических устройств в базисе ИЛИ_НЕ и И-НЕ

Построение логического устройства на элементах ИЛИ-НЕ может быть выполнено при следующей последовательности действий: заданная функция минимизируется с получением МКНФ; производится запись полученного логического выражения через операции ИЛИ-НЕ.

Рассмотрим последовательность синтеза на примере построения логического устройства, реализующего функцию, приведенную в табл. 3.28.

Для минимизации функции воспользуемся методом Вейча. В табл. 3.29 приведена карта Вейча для рассматриваемой функции.

Таблица 3.28
	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
	0	0	1	1	0	0	0	1	1	1	0	0	1	1	0	1

---

Смотрите также файлы

• Лекции, напишите эссе Условия профессионального развития личности.docx

• Задача по теме 13 раздела 2 Совершенная конкуренция объем выпуска.docx

• Интерпретация художественного текста. Вопрос 1.doc

• Доклад по дисциплине избранные главы биоорганической химии.docx

• управление персоналом 3.docx