ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.03.2024
Просмотров: 78
Скачиваний: 0
Лабораторна робота №3 Побудова довірчих інтервалів для прогнозованих значень, що отримуються при використанні регресивних моделей.
Мета роботи: Засвоїти методику побудови довірчих інтервалів для умовного математичного сподівання та окремих значень залежної змінної.
Теоретичні відомості
Регресійний аналіз знайшов широке використання в прогнозуванні. Прогноз отримують шляхом підстановки в регресій не рівняння з чисельно оціненими параметрами значень пояснюючих змінних. При цьому стверджується, що дане співвідношення між змінними з притаманним йому розкидом фактичних значень має місце і при нових умовах. Прогнозна оцінка може бути отримана при інтерполюванні та при екс прополюванні. Побудовані довірчі інтервали можуть бути використані в прогнозуванні. Розрахунок довірчих інтервалів дозволяє визначити область, в якій сподіваються буде значення величини, що прогнозується.
Надійність оцінки визначається ймовірністю, з якою стверджується, що побудований за результатами вибірки довірчий інтервал містить невідомий параметр називають довірчою і позначають Р. Ризик помилки визначається рівнем значущості α, який також називається довірчим рівнем, що відповідає даному інтервалу: α=1-Р. в економічних дослідженнях частіше за все довірча ймовірність вибирається рівною 0,95 або 95%. Тоді ризик помилки складає 5% (α=0,05).
Довірчий інтервал – це інтервал, який при заданому рівні значущості α покриває істинне значення регресії (умовного математичного сподівання змінної Y). Інтервальна оцінка істинних значень регресії при фіксованих значенням пояснюючих змінних Xi .
Довірчий інтервал для умовного математичного сподівання
Значення регресії за своїм характером є усередниними величинами, що розраховуються на основі отриманого емпіричного зв‘язку при кожному фіксованому значенні пояснюючої змінної. Як усі середні, кожне значення регресії є випадковою величиною. Вибіркові середні розташовані навколо середньої генеральної сукупності, яка в даному випадку є вірним значенням середньої залежної змінної, що досліджується (умовного математичного сподівання).
В математичній статистиці під регресією випадкової змінної Y на змінні Xk розуміють умовне математичне сподівання, тобто Y буде мати певне значення, якщо змінні Xk будуть мати визначенні значення.
Позначимо
![]() –
значення регресії генеральної сукупності
в точці і ,
–
значення регресії генеральної сукупності
в точці і ,
![]() –оцінка значення
регресії в точці і, що отримується за
методом найменших квадратів
–оцінка значення
регресії в точці і, що отримується за
методом найменших квадратів
Довірчий інтервал
для одного істинного значення регресії
![]() при заданому рівні значущості α і
фіксованих значеннях пояснюючих зміннихXi
визначається
за формулою:
при заданому рівні значущості α і
фіксованих значеннях пояснюючих зміннихXi
визначається
за формулою:
![]()
де
![]() -
квантільt-розподілу
при заданому рівні значущості α і
кількості ступені рівності f=n-m-1,
де n
- кількість спостережень, а m
– кількість змінних. (Знаходиться за
статистичними таблицями);
-
квантільt-розподілу
при заданому рівні значущості α і
кількості ступені рівності f=n-m-1,
де n
- кількість спостережень, а m
– кількість змінних. (Знаходиться за
статистичними таблицями);
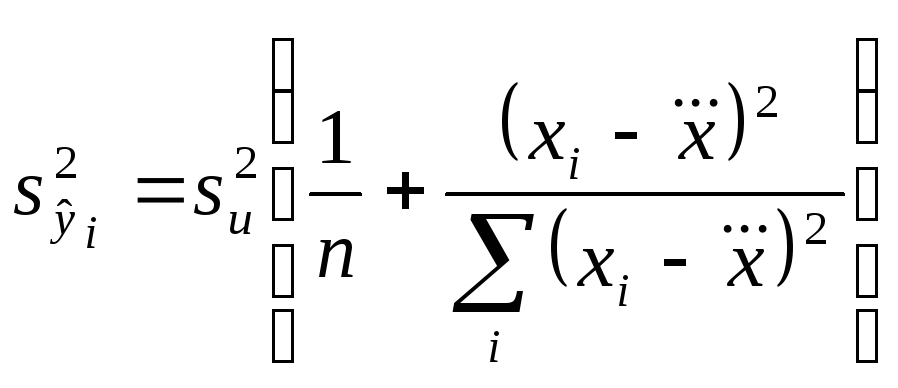 –оцінка дисперсії
простої лінійної регресії,
–оцінка дисперсії
простої лінійної регресії,
![]() -
дисперсія залишків (
-
дисперсія залишків (![]() )
)
Довірчі інтервали для окремих значень залежної змінної
Часто для досліджень необхідно побудувати довірчий інтервал не для середніх, а для індивідуальних значень залежної змінної. Довірчі інтервали для окремих значень залежної змінної ще називають довірчими інтервалами для прогнозів індивідуальних значень Yi.
Розглянемо моделі довірчих інтервалів , всередині яких з деяким ступенем достовірності , що обумовлений рівнем значущості α, буде знаходитись окреме значення Yi залежної змінної, що відповідає значенню Хі незалежної змінної.
Модель1. ( наближений спосіб побудови довірчих границь)
![]() ,
,
де
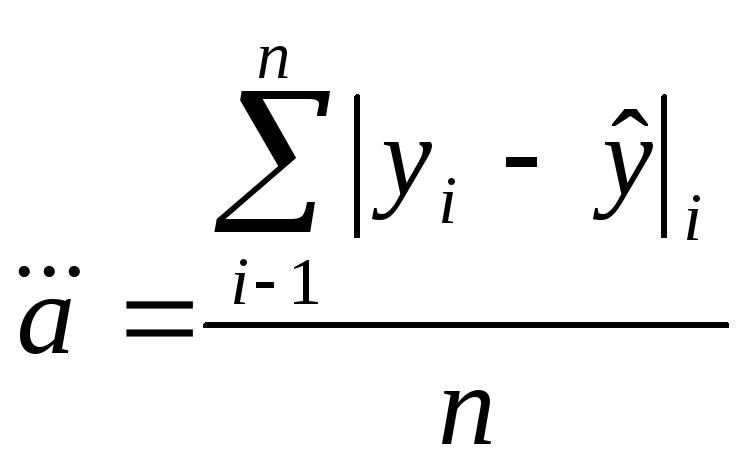
Цей спосіб є досить простим, але неможливо вказати ступінь достовірності потрапляння значень в ці межі.
Модель2. (враховується стандартне відхилення залишків)
![]()
де λα– квантіль нормального розподілу при заданому значенні рівня значущості α (вибирається з статистичних таблиць)
Молодь 3. (враховується стандартне відхилення похибки прогнозу)
![]()
де
![]() -
квантільt-розподілу
при заданому рівні значущості α і
кількості ступені рівності f=n-m-1,
де n
- кількість спостережень, а m
– кількість змінних. (Знаходиться за
статистичними таблицями);
-
квантільt-розподілу
при заданому рівні значущості α і
кількості ступені рівності f=n-m-1,
де n
- кількість спостережень, а m
– кількість змінних. (Знаходиться за
статистичними таблицями);
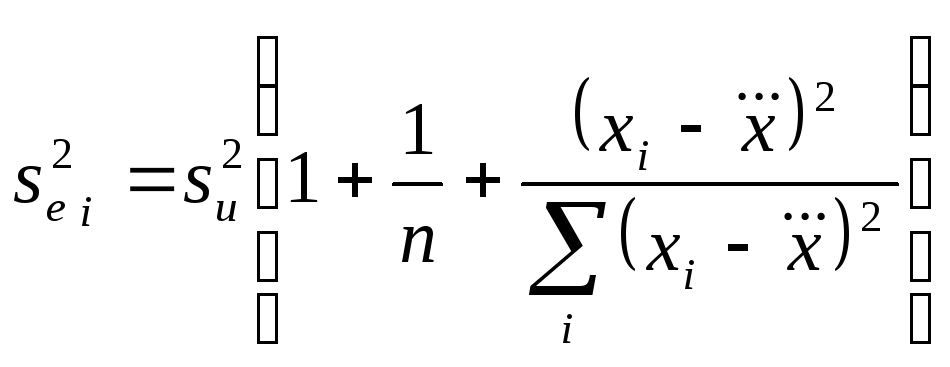 –оцінка дисперсії
простої лінійної регресії,
–оцінка дисперсії
простої лінійної регресії,
![]() –помилка прогнозу.
–помилка прогнозу.
Відносно цього інтервалу з ймовірністю Р=1-α можна стверджувати, що він містить фактичне значення залежної змінної Yi, що відповідають одночасним спостереженням над пояснюючими змінними Хі , або в середньому (1-α)100% всіх можливих значень Yi , що відповідають Хі , потраплять в цей інтервал.
Приклади використання.
Приклад 1.
Рівняння регресії, що виражає залежність експорту зернових культур від рівня урожайності наступне:
Y=7,0356+0,5435*x
![]() t12;0.05=2.179
t12;0.05=2.179
Таблиця 1.
Визначення довірчих границь для істинних значень простої лінійної регресії
|
I |
Xi |
Yi |
|
ui |
ui2 |
|
|
t12;0.05 |
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
1 |
32 |
20 |
24,4276 |
-4,4276 |
17,9776 |
388,4841 |
0,9692 |
2,1119 |
22,3157 |
26,5395 |
|
2 |
30 |
24 |
23,3406 |
0,6594 |
0,4348 |
471,3241 |
1,0360 |
2,2575 |
21,0831 |
25,5981 |
|
3 |
36 |
28 |
26,6016 |
1,3984 |
1,9555 |
246,8041 |
0,8428 |
1,8364 |
24,7652 |
28,4380 |
|
4 |
40 |
30 |
28,7756 |
1,2244 |
1,4991 |
137,1241 |
0,7299 |
1,5905 |
27,1850 |
30,3662 |
|
5 |
41 |
31 |
29,3186 |
1,6814 |
2,8271 |
114,7041 |
0,7047 |
1,5356 |
27,7830 |
30,8542 |
|
6 |
47 |
33 |
32,5806 |
0,4194 |
0,1759 |
22,1841 |
0,5890 |
1,2835 |
31,2971 |
33,8641 |
|
7 |
56 |
34 |
37,4716 |
-3,4716 |
12,0520 |
18,4041 |
0,5838 |
1,2722 |
36,994 |
38,7438 |
|
8 |
54 |
37 |
36,3846 |
0,6154 |
0,3788 |
5,2441 |
0,5653 |
1,2318 |
35,1528 |
37,6164 |
|
9 |
60 |
38 |
39,6456 |
-1,6456 |
2,7080 |
68,7241 |
0,6498 |
1,4159 |
38,2297 |
41,0615 |
|
10 |
55 |
40 |
36,9276 |
3,0724 |
9,4396 |
10,8241 |
0,5732 |
1,2491 |
35,6768 |
38,1767 |
|
11 |
61 |
41 |
40,1896 |
0,8104 |
0,6567 |
86,3041 |
0,6713 |
1,4628 |
38,7268 |
41,6524 |
|
12 |
67 |
43 |
43,4496 |
-0,4496 |
0,2021 |
233,7841 |
0,8302 |
1,8089 |
41,6407 |
45,2585 |
|
13 |
69 |
45 |
44,5376 |
0,4624 |
0,2138 |
298,9441 |
0,8914 |
1,9424 |
42,5952 |
46,4800 |
|
14 |
76 |
48 |
48,3416 |
-0,3416 |
0,1167 |
590,0041 |
1,1249 |
2,4511 |
45,8905 |
50,7927 |
|
Σ |
724 |
492 |
492 |
0 |
52,2639 |
2692,8574 |
|
|
|
|
|
15 |
51 |
|
34,7541 |
|
|
0,5041 |
05585 |
1,2169 |
33,5372 |
35,9710 |
|
16 |
78 |
|
49,4286 |
|
|
691,1641 |
1,1954 |
2,6047 |
46,8239 |
52,0333 |
Приклад 2.
Визначимо для залежності експорту зернових культур від рівня урожайності довірчі границі для окремих значень Y, що розраховані за 3-ю моделлю.(таблиця 2)
Таблиця 2.
Визначення довірчих границь для прогнозу індивідуальних значень Y у випадку простої лінійної регресії
|
i |
|
t12;0.05 |
|
|
|
1 |
2.3010 |
5,0139 |
19,4137 |
29,4415 |
|
2 |
2.3299 |
5,0768 |
18,2636 |
28,4174 |
|
3 |
2.2507 |
4,9042 |
11,6974 |
31,5058 |
|
4 |
2.2109 |
4,8176 |
23,9580 |
33,5932 |
|
5 |
2.2027 |
4,7997 |
24,5189 |
34,1183 |
|
6 |
2.1685 |
4,7251 |
27,8555 |
37,3057 |
|
7 |
2.1671 |
4,7220 |
32,7496 |
42,1936 |
|
8 |
2.1621 |
4,7113 |
31,6733 |
41,0959 |
|
9 |
2.1858 |
4,7628 |
34,8828 |
44,4084 |
|
10 |
2.1642 |
4,7159 |
32,2117 |
41,6435 |
|
11 |
2.1923 |
4,7769 |
35,4127 |
44,9665 |
|
12 |
2.2460 |
4,8940 |
38,5556 |
48,3436 |
|
13 |
2.2693 |
4,9449 |
39,5927 |
49,4825 |
|
14 |
2.3708 |
5,1659 |
43,1757 |
53,5075 |
|
15 |
2.1604 |
4,7075 |
30,0466 |
39,4616 |
|
16 |
2.4050 |
5,2406 |
44,1880 |
54,6692 |