ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 209
Скачиваний: 0
СОДЕРЖАНИЕ
Лекции по общей теории статистики
Тема 1. Введение. Предмет и метод статистической науки
1.1. История развития статистической науки
1.2. Предмет и метод статистической науки
1.3. Организация и функции статистических служб
Тема 2. Статистическое наблюдение
2.1. Статистическое наблюдение.
2.2. Сводка и группировка статистических данных
2.3. Принципы построения статистических группировок
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
3.3. Средние структурные величины
4.1. Понятие вариационных рядов.
Графическое отображение вариационных рядов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
5.2. Закон больших чисел и предельные теоремы
5.3 Формы организации выборочного наблюдения
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Оценка линейного коэффициента корреляции
7.2 Методы анализа тенденций рядов динамики
7.3. Статистические методы прогнозирования экономических показателей
8.2. Общие индексы количественных показателей
8.3. Общие индексы качественных показателей
8.4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов
2.3. Принципы построения статистических группировок
1. Выбор группировочного признака– признака, по которому производится разбиение совокупности на отдельные группы. В качестве признака необходимо использовать существенные обоснованные признаки.Группировочный признак– это основание (свойство объекта) для разделения объектов на группы.
Признаки различаются:
по форме выражения (атрибутивныеиколичественные);
по характеру колебания (альтернативные«да», «нет»;множественные);
по роли во взаимосвязи явлений (результативные– могут меняться в зависимости от ситуации и целей анализа;факторные– воздействующие на другие признаки).
2. Определение количества групп.Если в основание группировки положен атрибутивный признак, то количество групп будет столько, сколько существует градаций (уровней) данного признака. Если основание группировки – количественный признак, то при определении количества групп в каждом конкретном случае следует исходить не только из степени колеблемости признака, но и из особенностей объекта и цели исследования.
Если совокупность состоит из большого числа единиц и распределение единиц по группировочному признаку близко к нормальному, для определения количества групп (n) используют формулу Стерджесса:
n = 1+3,322·lg N, (2.1)
где N– численность единиц совокупности. Количество групп всегда округляется в большую сторону.
3. Определение интервала группировки.Интервал– это значение варьирующего признака, лежащее в определенных границах.
Если вариация признака происходит в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами:
![]() , (2.2)
, (2.2)
где h– величина интервала;
xmax,xmin– максимальное и минимальное значения группировочного признака в совокупности;
n– число групп.
Интервалы могут быть двух видов:
закрытыми, когда у интервала указаны обе границы;
открытыми, когда у первого интервала указана верхняя граница, а у последнего – нижняя (например, в таблице 2.3, 1-я группа населения по размеру среднедушевого дохода – до 1000 руб.; последняя – 10000 и более).
Возможно построение вторичных группировок. Основные задачи, вторичной группировки:
приведение данных к сопоставимым результатам;
укрупнение интервалов;
долевая перегруппировка (образование новых групп с меньшими интервалами).
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
Абсолютными в статистике называются суммарные обобщающие показатели, характеризующие размеры, объемы, уровни, мощности, темпы и др. изменения величин. Абсолютные показатели являются именованными числами, т.е. измеримы. Существуют: натуральные, стоимостные и условно-натуральные (условное топливо, эталонные лошадиные силы) измерители. Они служат для описания фактического состояния объекта, установления плановых и прогнозных значений. Абсолютные показатели могут быть сравнимы в разные периоды времени (прошлый, настоящий, будущий).
Абсолютные показатели позволяют точно характеризовать объект в данный момент времени, но должны уточняться в динамике (сопоставимые цены, инвестиции с учетом инфляции и т.д.).
Относительные статистические величины– это показатели в виде коэффициентов, характеризующих долю отдельных частей, изучаемой совокупности во всем ее объеме.
Относительные показатели при исследовании экономических явлений и процессов изучаются совместно с абсолютными показателями и обеспечивают сопоставимость сравниваемой и базовой величин.
Относительный показатель динамики (ОПД) представляет собой отношение уровня исследуемого процесса или явления за данный период времени (по состоянию на данный момент времени) к уровню этого же процесса или явления в прошлом:
ОПД
![]() или ОПД
или ОПД
![]() . (3.1)
. (3.1)
Относительный показатель структуры(ОПС) представляет собой отношение структурных частей изучаемого объекта и их целого:
ОПС![]() . (3.2)
. (3.2)
Выражается относительный показатель структуры в долях единицы или в процентах. Рассчитанные величины, соответственно называемые долями или удельными весами, показывают, какай долей обладает или какой удельный вес имеет та или иная часть в общем итоге.
Относительный показатель координации(ОПК) представляет собой отношение одной части совокупности к другой части этой же совокупности:
ОПК
![]() . (3.3)
. (3.3)
При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают величину, отражающую во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда – на 100, 1000 и т.д. единиц) базисной структурной части.
Относительный показатель сравнения(ОПСр) представляет собой отношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.):
ОПСр
![]() . (3.4)
. (3.4)
Относительный показатель интенсивности(ОПИ) характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:
ОПИ
![]() , (3.5)
, (3.5)
где xA – показатель, характеризующий явление А;
YA – показатель, характеризующий среду распространения явления А.
Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому, наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах и т.п.
Разновидностью относительных показателей интенсивности являются относительные показатели уровня экономического развития, характеризующие производство продукции в расчете на душу населения и играющие важную роль в оценке развития экономики государства. Так как объемные показатели производства продукции по своей природе являются интервальными, а показатель численности населения – моментным, в расчетах используют среднюю за период численность населения.
Относительные показатели плана и реализации планаиспользуются для целей планирования и сравнения реально достигнутых результатов с ранее намеченными.
ОПП
![]() , (3.6)
, (3.6)
где ОПП – относительный показатель плана;
![]() – уровень, планируемый наi+1
период;
– уровень, планируемый наi+1
период;
xi– уровень, достигнутый вi-м периоде.
ОПРП
![]() , (3.7)
, (3.7)
где ОПРП – относительный показатель реализации плана;
xi– уровень, достигнутый в (i+1)-м периоде.
ОПП характеризует напряженность плана, т.е. во сколько раз намечаемый объем производства превысит достигнутый уровень или сколько процентов от этого уровня составит. ОПРП отражает фактический объем производства в процентах или коэффициентах по сравнению с плановым уровнем.
3.2. Средние величины
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Все виды средних делятся на:
степенные(аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);
структурные(позиционные) средние (мода и медиана) – применяются для изучения структуры рядов распределения.
Средняя степенная (при различной величине k) определяется:
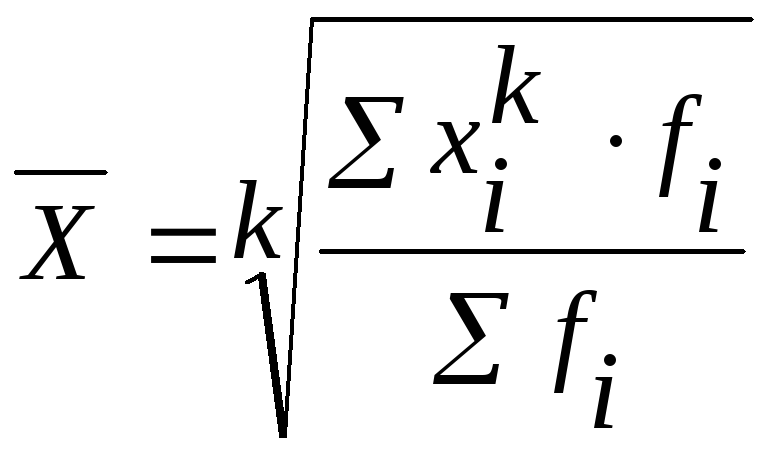 (3.8).
(3.8).
Таблица 1.1 - Виды средних степенных величин
|
№ |
Наименование средней |
Формула средней |
Когда используется |
|
1 |
Средняя арифметическая простая (невзвешенная) |
где xi
– i-й вариант осредняемого признака
( n – число вариант |
Используется, когда расчет осуществляется по несгруппированным данным |
|
2 |
Средняя арифметическая взвешенная |
где fi – частота повторяемости i-го варианта |
Используется, когда данные представлены в виде рядов распределения или группировок |
|
3 |
Средняя гармоническая взвешенная |
|
Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
|
4 |
Средняя гармоническая невзвешенная |
|
Используется в случае, когда веса равны |
|
5 |
Средняя геометрическая невзвешенная |
|
Используется в анализе динамики для определения среднего темпа роста |
|
6 |
Средняя геометрическая взвешенная |
|
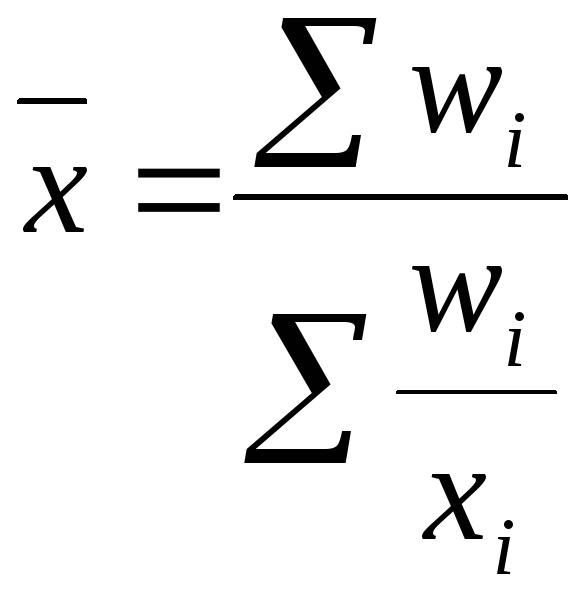 (3.11), где
(3.11), где