ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.03.2024
Просмотров: 229
Скачиваний: 0
СОДЕРЖАНИЕ
Лекции по общей теории статистики
Тема 1. Введение. Предмет и метод статистической науки
1.1. История развития статистической науки
1.2. Предмет и метод статистической науки
1.3. Организация и функции статистических служб
Тема 2. Статистическое наблюдение
2.1. Статистическое наблюдение.
2.2. Сводка и группировка статистических данных
2.3. Принципы построения статистических группировок
Тема 3. Статистические показатели
3.1. Абсолютные и относительные статистические показатели
3.3. Средние структурные величины
4.1. Понятие вариационных рядов.
Графическое отображение вариационных рядов
4.3. Виды дисперсий в совокупности, разделенной на части. Правило сложения дисперсий
Тема 5. Выборочное наблюдение в статистике
5.1. Сущность выборочного наблюдения.
5.2. Закон больших чисел и предельные теоремы
5.3 Формы организации выборочного наблюдения
Тема 6. Статистические методы изучения взаимосвязи социально-экономических явлений
6.1. Сущность корреляционной связи.
Оценка линейного коэффициента корреляции
7.2 Методы анализа тенденций рядов динамики
7.3. Статистические методы прогнозирования экономических показателей
8.2. Общие индексы количественных показателей
8.3. Общие индексы качественных показателей
8.4. Индексы переменного и фиксированного состава. Индекс структурных сдвигов
Свойства средней арифметической
Средняя арифметическая постоянной величины равна самой величине.
Если все варианты xiувеличить (уменьшить) на одно и тоже числоc,
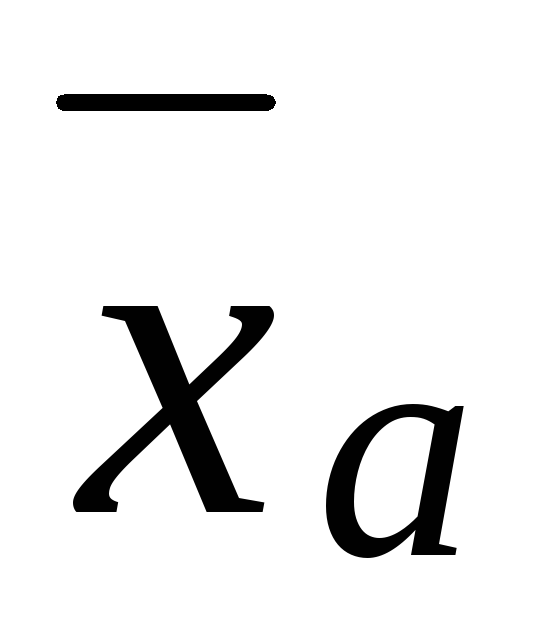 увеличится (уменьшится) на то же число.
увеличится (уменьшится) на то же число.
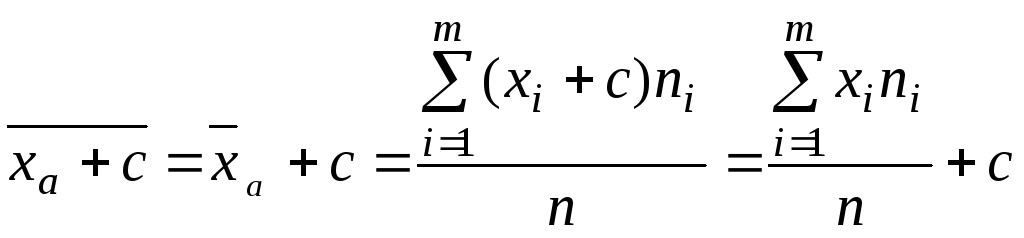 . (3.17)
. (3.17)
Если все варианты xiувеличить (уменьшить) в одно и то же число разk,
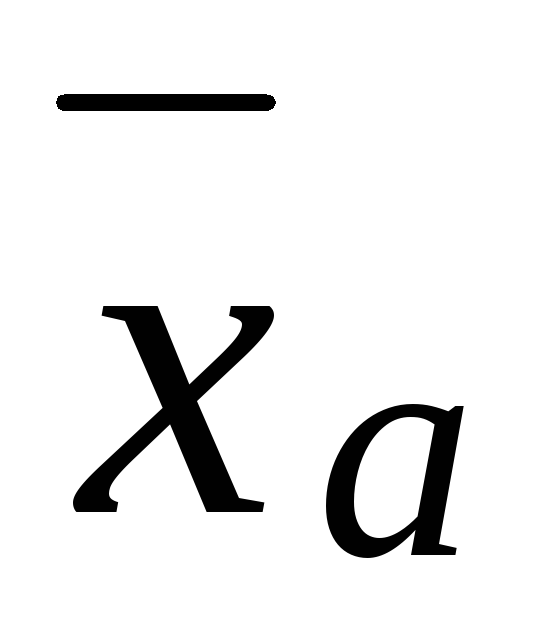 увеличится (уменьшится) в то же число
раз.
увеличится (уменьшится) в то же число
раз.
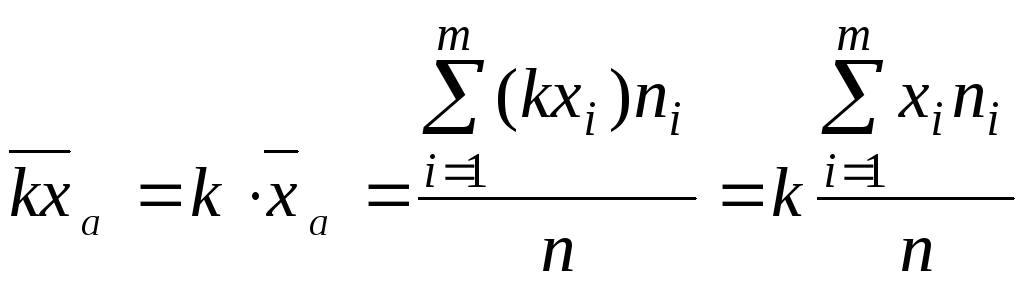 . (3.18)
. (3.18)
Средняя арифметическая отклонений вариантов от средней арифметической равна 0.
![]() . (3.19)
. (3.19)
По
свойству 2 при
![]() :
:![]() .
.
3.3. Средние структурные величины
В условиях недостаточности средних используют структурные средние величины – моду и медиану.
Медиана(Ме) – это вариант, который находится а середине вариационного ряда. Медиана делит ряд на две равные (по числу наблюдений) части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера.
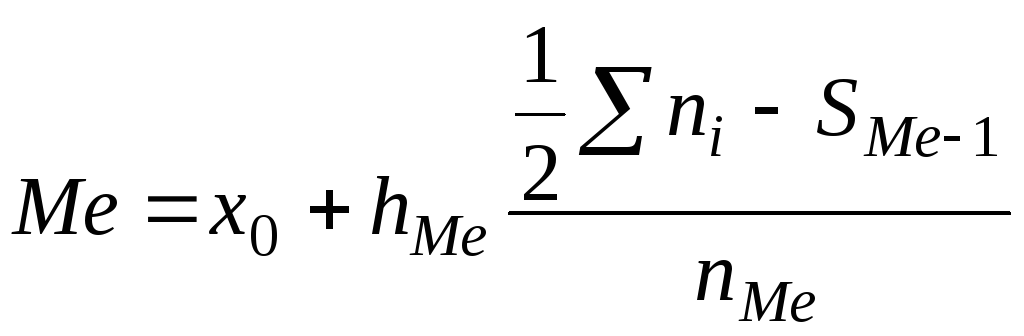 , (3.20)
, (3.20)
где х0– нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот);
![]() – величина медианного интервала;
– величина медианного интервала;
![]() – накопленная частота интервала,
предшествующего медианному;
– накопленная частота интервала,
предшествующего медианному;
![]() – частота медианного интервала.
– частота медианного интервала.
Главное
свойство медианызаключается в том,
что сумма абсолютных отклонений значений
признака от медианы меньше, чем от любой
другой величины:![]() .
.
Модой (Мо) вариационного ряда называется вариант, которому соответствует наибольшая частота.
Для вычисления моды в интервальномряду сначала находится модальный интервал, имеющий наибольшую частоту (или наибольшую плотность распределения – отношение частоты интервала к его величинеni/hi– в интервальном ряду с неравными интервалами), а значение моды определяется линейной интерполяцией:
![]() , (3.21)
, (3.21)
где хо –нижняя граница модального интервала;
![]() – величина модального интервала;
– величина модального интервала;
![]() – частота модального интервала;
– частота модального интервала;
![]() – частота интервала предшествующая
модальныму;
– частота интервала предшествующая
модальныму;
![]() – частота интервала следующего за
модальным.
– частота интервала следующего за
модальным.
Тема 4. Вариационные ряды
4.1. Понятие вариационных рядов.
При изучении совокупности интересующий нас признак у различных единиц совокупности принимает различные значения, т.е. он имеет некоторую вариацию.
Вариацией признаканазывается наличие различий в численных значениях признаков у отдельных единиц совокупности.
Чтобы выявить характер распределения единиц совокупности по варьирующим признакам, определить закономерности в этом распределении, строят ряды распределения единиц совокупностей по какому-либо варьирующему признаку.
Ряды распределения, построенные по количественному признаку называются вариационными.
При анализе вариационных рядов решают следующие задачи:
1) Определение меры вариации, т.е. количественное измерение степени колеблемости признака. Это позволяет сравнивать различные совокупности между собой по степени рассеяния и отслеживать уровень вариации признака одной и той же совокупности в различные периоды.
2) Исследование закономерностей вариациив статистических совокупностях для изучения причин, вызывающих вариацию.
Для описания статистических распределений обычно используются следующие видыхарактеристик (показателей):
1) средние величины;
2) характеристики вариации (рассеяния);
3) характеристики дифференциации и концентрации;
4) характеристики формы распределения.
Графическое отображение вариационных рядов
Вариационный ряд по своей конструкции имеет 2 характеристики:
значения варьирующего признака – вариантыxi,i= 1,2,…,m;
число случаев вариантов: абсолютные – частотыni(fi), относительные –частостиwi(относительные доли частот в общей сумме частот).
Тогда можно сказать, что вариационный ряд– это ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частостей).
Вариационные ряды по способу построения бывают дискретные и интервальные.
Дискретный вариационный ряд можно рассматривать как такое преобразование ранжированного ряда, при котором перечисляются отдельные значения признака и указывается их частота.
Если число вариантов велико или признак имеет непрерывную вариацию, то строится интервальныйвариационный ряд, в котором отдельные варианты объединяются в интервалы (группы).
4.2. Показатели вариации
Вариацией называется изменяемость, колеблемость величины признака. Вариация проявляется в отклонениях от средних и зависит от множества факторов, влияющих на социально-экономическое явление. Вариация бывает случайной и систематической, существует в пространстве и во времени.
Таблица 4.1 - Показатели вариации
|
|
Показатель |
Формула расчета показателя |
|
|
Абсолютные |
Размах |
|
|
|
Среднее линейное отклонение |
|
|
|
|
Дисперсия |
σ2 |
|
|
|
Среднее квадратическое отклонение |
|
|
|
|
относительные |
Коэффициент вариации |
|
|
|
Линейный коэффициент вариации |
|
||
|
Коэффициент осцилляции |
|
||
Относительные показатели строятся с учетом базы (в виде средней), выражаются в процентах и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации
![]() . (4.11)
. (4.11)
 (4.2)
(4.2)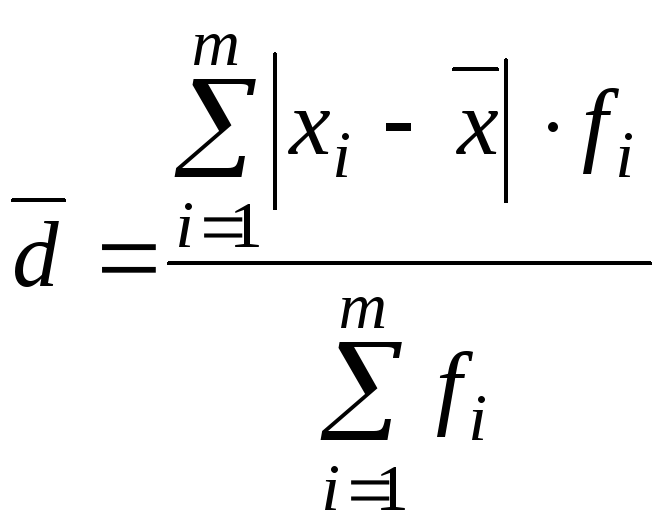 (4.3)
(4.3)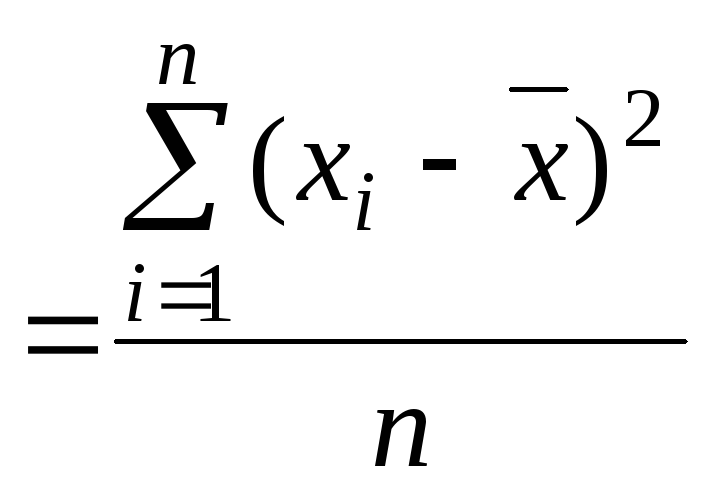 (4.4)
(4.4) (4.5)
(4.5)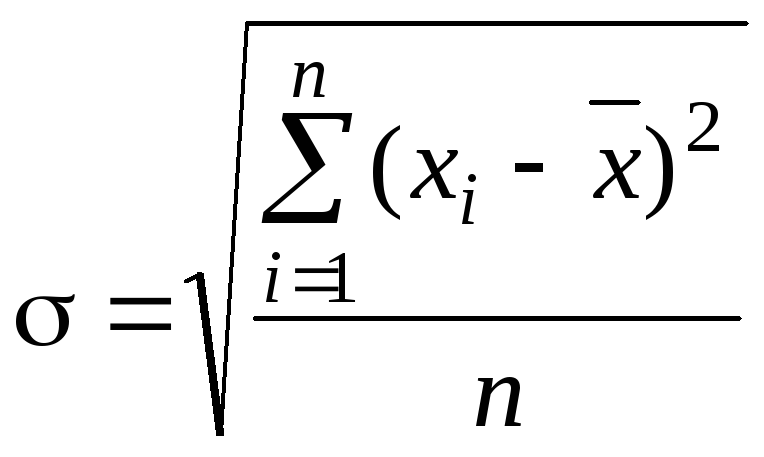 (4.6)
(4.6)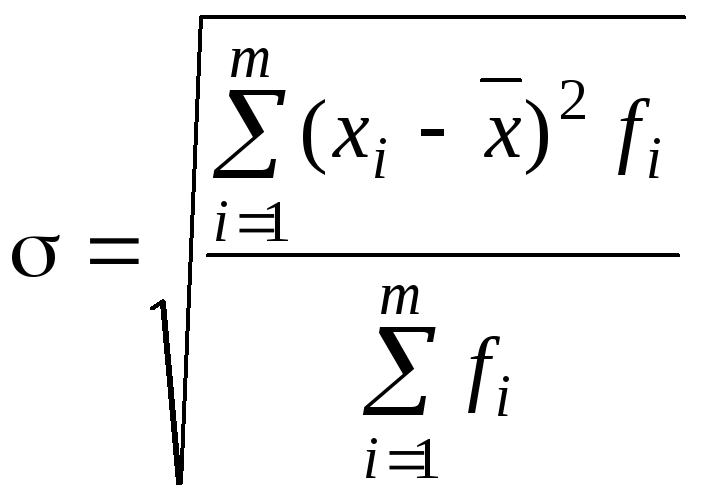 (4.7)
(4.7)