Северо-Кавказский горно-металлургический институт

(государственный технологический университет)

Кафедра автоматизированной обработки информации

КУРСОВАЯ РАБОТА

на тему:

"Нахождение единой матрицы преобразований"

Выполнила: студентка гр. ИВб-11-2

Глотова А.В.

Проверила: Соколова Е.А.

Владикавказ-2013

Задание: Составить единую матрицу преобразований для поворота графического объекта относительно отрезка на заданный угол и программно реализовать.

СОДЕРЖАНИЕ

Введение		4 стр.
1.	Теоретическая часть
	1.1. Аналитический обзор	6 стр.
	1.2. Содержательная постановка задачи	8 стр.
2.	Практическая часть
	2.1. Алгоритм	9 стр.
	2.1. Программная реализация	10 стр.
	2.2. Пример	13 стр.
Заключение		18 стр.
Литература		20 стр.
Приложения		21 стр.

---

ВВЕДЕНИЕ

Цель курсовой работы: вычисление единой матрицы преобразований для поворота графического объекта относительно отрезка.

Задачи курсовой работы:

1. Изучение теоретических основ вращения графических объектов.

2. Расчет матриц поворота для различных осей.

Разработка и программная реализация алгоритма нахождения единой матрицы преобразований.

3. Работа с файлами для предоставления информации о расчете.

4. Формирование навыков работы с литературой, анализа полученных данных и умения построения на их основе логических заключений.

В настоящее время трудно представить человека, не знакомого с понятием компьютерной графики. Мы сталкиваемся с ним постоянно: при распечатке плакатов, обработке в Photoshop фотографий, работая с любым изображением.

Компьютерная графика - это область деятельности, в которой компьютеры используются в качестве инструмента как для создания изображений, так и для обработки визуальной информации, полученной из реального мира.

Этот раздел включает в себя описание разных типов графических изображений (растровая, векторная, фрактальная); методов их обработки (масштабирования, изменения цвета, яркости, контрастности, поворот изображения на заданный угол, наложение фильтров); алгоритмы сжатия изображений (RLE, JPEG,LZW), алгоритмы построения примитивов (ЦДА, алгоритм Брезенхема для окружности) и т.д. Современное программное обеспечение и стремительно развивающиеся возможности видеокарт позволяют обрабатывать огромные объемы графической информации и создавать собственные программные продукты, реализующие методы обработки изображений различного масштаба и любого расширения. В данном курсовом проекте разработана программа поворота изображения относительно отрезка, представляющая собой огромные расчеты с использованием матриц, время которых значительно снижено за счет использования компьютерной техники.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. АНАЛИТИЧЕСКИЙ ОБЗОР

Поворот изображения относительно отрезка - это пересчет его координат с помощью единой матрицы преобразований.

Единая матрица преобразований - это матрица, при умножении на которую координаты начальной и конечной точки заданного отрезка остаются неизменными, а координаты поворачиваемого изображения пересчитываются в зависимости от заданных условий (угла и отрезка), после чего графический объект перерисовывается

---

Для получения единой матрицы преобразований используются:

• матрицы поворота относительно осей - ортогональные матрицы, которые используются для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.

1) относительно оси ОХ:

,

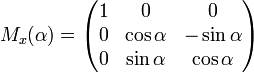
2) относительно оси ОУ:

,

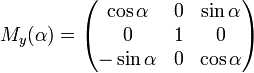3) относительно OZ:

.

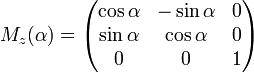• Инцидентная матрица

• Проекция - векторной проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси.

• Обратная матрица - такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E.

1.2. СОДЕРЖАТЕЛЬНАЯ ПОСТАНОВКА ЗАДАЧИ

Дан отрезок ОВ, ось и задан угол поворота изображения α. Необходимо, основываясь на исходных данных, построить единую матрицу преобразований для поворота изображения на заданный угол относительно отрезка ОВ. Использовать при вычислениях матрицы поворота М1(Х), М2 (У), М3 (Z), а также обратные им матрицы М5, М6, М7.

2. ПРАКТИЧЕСКАЯ ЧАСТЬ

2.1. АЛГОРИТМ

П1. Ввод исходных данных.

П2. Совмещение начальной точки отрезка с началом координат посредством инцидентной матрицы.

П3. Нахождение новой конечной точки путем умножения её координат на инцидентную матрицу.

П4. Создание проекции на одну из осей.

П5. Рассчет гипотенузы

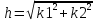
где k1, k2 - значения двух свободных осей.

Нахождение Cos и Sin.

П6. Создание матрицы М2 с помощью соответствующей матрицы поворота Rx, Ry, Rz.

П7. Перерасчет координат конечной точки В.

П8. Используя полученные данные, повторяем шаги П4-П7 и строим матрицу М3.

---

П9. Находим матрицу поворота М4 в соответствии с заданным углом и осью.

П10. С помощью метода Гаусса или алгебраических дополнений вычисляем обратные матрицы к М1,М2,М3. П11. Находим произведение всех полученных матриц:

Ms=M1*M2*...*M7

П12. Проверяем на правильность результат: если при умножении исходных координат конечной точки В на единую матрицу преобразований результат отличается от исходных данных на 0,001, то точность достигнута и матрица верна. В противном случае рекомендуется еще раз пройти пункты П1-П11.

2.2. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

Алгоритм нахождения единой матрицы преобразований для поворота изображения реализован в среде разработки Visual Studio 2013 на языке C#.

Для внешнего облика программы были использованы следующие компоненты и их свойства(рис.1):

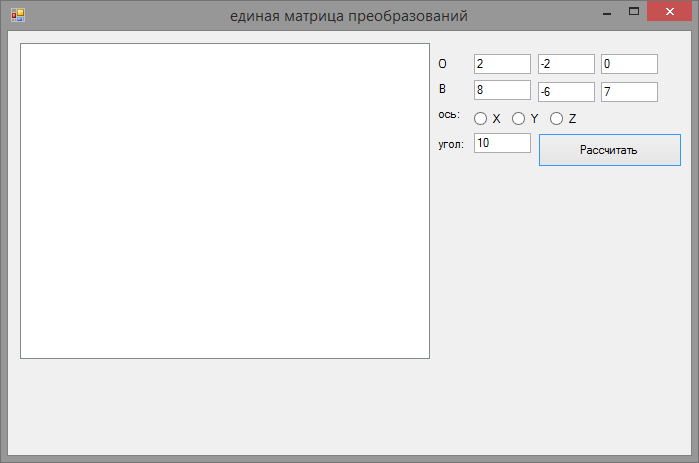
Рис.1 Внешний вид программы

1. – textBox – представляет собой текстовое поле, в которое вносятся значения координат отрезка и угол поворота. Задействованные свойства:

- Text - меняет содержимое поля.

2. – ListBox – текстовой поле, позволяющее выводить большой объем данных. В программе необходимо для вывода результата расчетов.

3. – button – кнопка, при нажатии на которую происходит вычислительный процесс.

4,5,6 – radiobutton – кнопки, позволяющие выбрать только одно из значений. В программе служат для определения оси поворота.

В программе задействованы следующие переменные:

а – угол поворота.

двумерные массивы вещественных чисел О и В - координаты отрезка.

двумерный вещественный массив М1 - инцидентная матрица.

двумерные вещественные массивы М2,М3,М4 - матрицы поворота.

двумерные вещественные массивы М5,М6,М7 - обратные матрицы.

двумерный вещественный массив С - суперматрица.

В программе используются следующие процедуры и функции:

Комплекс процедур по нахождению обратных матриц методом алгебраических дополнений:

• public static double[,] Inverse(double[,] matrix)

• public static double Determinent(double[,] matrix)

• public static double[,] AlgebraicComplement(double[,] matrix)

• public static double[,] Multiply(double[,] matrix, double number)

• public static double[,] Minor(double[,] matrix, int row, int column)

• private static int Signum(int number)

• public static double[,] Transpose(double[,] matrix)

---

Процедуры умножения матриц:

• void MultB(double[,] K,double[,] L)

• void MultAll(double [,] K,double [,] L)

Процедуры нахождения матриц поворота:

• void MatrpZ(double co1, double si1)

• void MatrpY(double co1, double si1)

• void MatrpX(double co1,double si1)

Процедура нахождения инцидентной матрицы:

• void Matr1()

Основные процедуры расчета в зависимости от исходных данных, включают в себя остальные подпрограммы: - void MatrX()

• void MatrY()

• void MatrZ()

Процедура нажатия кнопки:

• private void button1_Click(object sender, EventArgs e)

2.3. ПРИМЕР

Для проверки работы программы решим один пример вручную, а потом программно и сравним результаты.

В качестве исходных данных используем

Отрезок: О(2 0 -1) - В(8 6 -8)

Ось:У

Угол равен 60 градусам.

1) Совместим начало ОВ с началом координат, воспользовавшись инцидентной матрицей М1:

1 0 0 0

0 1 0 0

0 0 1 0

-2 0 1 1

Умножим координаты начальной и конечной точки на М1:

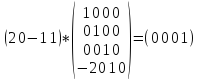
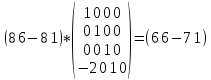
Найдем матрицу М2, построив проекцию отрезка на одну из осей:

Гипотенуза = 9,2195, Sin = -0,7593, Cos=0,6508

Применим соответствующую матрицу поворота Ry и получим матрицу М2:

0,650 0 0,759 0

0 1 0 0

-0,759 0 0,65 0

0 0 0 1

Умножаем координаты конечной точки отрезка на М2 аналогично пункту выше и получаем:

(9,2 6 0,0002 1)

Чтобы совместить отрезок с осью ОУ вновь находим создаем проекцию и вычисляем :

Гипотенуза = 11,0003, Sin = 0,8381, Cos=0,5454

Применим соответствующую матрицу поворота Rz и получим матрицу М3:

0,5454 0,8381 0 0

-0,8381 0,5454 0 0

0 0 1 0

0 0 0 1

Составим матрицу поворота M4 относительно оси ОY на угол 60 градусов.

0,5 0 -0,866 0

0 1 0 0

0,866 0 0,5 0

0 0 0 1

Найдем обратные матрицы:

М5:

0,545 -0,83 0 0

0,84 0,545 0 0

0 0 1 0

0 0 0 1

М6:

0,65 0 -0,75 0

---

Смотрите также файлы

• отчёт №3 Excel.docx

• отчёт №2.docx

• отчёт №2 Excel.docx

• отчёт №1.docx

• отчёт №1 Excel.docx