1) его малая ось видна из фокусов под углом в 60°;

2) отрезок между фокусами виден из вершин малой оси под прямым углом;

3) расстояние между дирек­трисами в три раза больше рас­стояния между фокусами;

4) отрезок перпендикуляра, опущенного из центра эллипса на его директрису, делится вер­шиной эллипса пополам.

467. Через фокус F эллипса проведён перпендикуляр к его большой оси (черт. 15). Опреде­лить, при каком значении эксцен­триситета эллипса отрезки и будут параллельны.

468. Составить уравнение эллипса с полуосями a, b и центром С(x₀ ; у ₀), если известно, что оси симметрии эллипса параллельны осям координат.

469. Эллипс касается оси абсцисс в точке А (3; 0) и оси орди­нат в точке В (0; —4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

470. Точка С (— 3; 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.

471. Установить, что каждое из следующих уравнений опреде­ляет эллипс, и найти координаты его центра С, полуоси, эксцен­триситет и уравнения директрис:

1) 5х² + 9у² — 30х + 18у + 9 = 0;

2) 16х² + 25у² + 32х — 100у — 284 = 0;

3) 4х² + 3у² — 8х + 12у —32 = 0.

472. Установить, какие линии определяются следующими урав­нениями:

1) ; 2) ;

3) ; 4) .

Изобразить эти линии на чертеже.

473. Составить уравнение эллипса, зная, что:

1) его большая ось равна 26 и фокусы суть F₁ (—10; 0), F₂ (14; 0);

2) его малая ось равна 2 и фокусы суть F₁(—1; —1), F₂ (1; 1);

3) его фокусы суть F₁ (2; ) , F₂ (2; ) эксцентриситет ;

---

4) его фокусы суть F₁ (l; 3), F₂ (3; 1) и расстояние между ди­ректрисами равно .

474. Составить уравнение эллипса, если известны его эксцентриситет , фокус F(-4; 1) и уравнение соответствующей ди­ректрисы x - 5 = 0.

475. Составить уравнение эллипса, если известны его эксцен­триситет фокус F(—4; 1) и уравнение соответствующей директрисы

y + 3 = 0

476. Точка А (— 3; — 5) лежит на эллипсе, фокус которого F(—1; —4), а соответствующая директриса дана уравнением

х — 2 = 0.

Составить уравнение этого эллипса.

477. Составить уравнение эллипса, если известны его эксцен­триситет , фокус F(3; 0) и уравнение соответствующей ди­ректрисы х + у — 1= 0.

478. Точка M₁ (2; —1) лежит на эллипсе, фокус которого F(l; 0), а соответствующая директриса дана уравнением 2х — у — 10 = 0. Составить уравнение этого эллипса.

479. Точка M₁ (3; —1) является концом малой оси эллипса, фо­кусы которого лежат на прямой у + 6 = 0.Составить уравнение этого эллипса, зная его эксцентриситет .

480. Найти точки пересечения прямой х + 2у — 7 = 0 и эллипса х² + 4у² = 25.

481. Найти точки пересечения прямой 3х + 10у — 25 = 0 и эллипса

482. Найти точки пересечения прямой 3х — 4у — 40 = 0 и эллипса

483. Определить, как расположена прямая относительно эллипса: пересекает ли, касается или проходит вне его, если прямая и эллипс заданы следующими уравнениями:

1) 2х—у —3 = 0, 2) 2х+у— 10 = 0,

3) 3х + 2у —20 = 0,

484. Определить, при каких значениях m прямая у = —k x + m: 1) пересекает эллипс ; 2) касается его; 3) проходит вне этого эллипса.

---

485. Вывести условие, при котором прямая y = kx + m касается эллипса

486. Составить уравнение касательной к эллипсу

в его точке M₁ (x₁; y₁).

487. Доказать, что касательные к эллипсу

проведённые в концах одного и того же диаметра, параллельны. (Диаметром эллипса называется его хорда, проходящая через центр.)

488. Составить уравнения касательных к эллипсу

параллельных прямой 3х + 2у + 7 = 0.

489. Составить уравнения касательных к эллипсу

х² + 4у² = 20,

перпендикулярных к прямой

2х —2у—13 = 0.

490. Провести касательные к эллипсу

параллельно прямой

4х —2у + 23 = 0

и вычислить расстояние d между ними.

491. На эллипсе

найти точку M₁, ближайшую к прямой

2х— 3у + 25 = 0,

и вычислить расстояние d от точки M₁ до этой прямой.

492. Из точки А () проведены касательные к эллипсу

Составить их уравнения.

493. Из точки С(10; —8) проведены касательные к эллипсу

Составить уравнение хорды, соединяющей точки касания.

494. Из точки Р(—16; 9) проведены касательные к эллипсу

Вычислить расстояние d от точки Р до хорды эллипса, соединяю­щей точки касания.

495. Эллипс проходит через точку А (4; —1) и касается пря­мой х + 4у—10 = 0. Составить уравнение этого эллипса при усло­вии, что его оси совпадают с осями координат.

496. Составить уравнение эллипса, касающегося двух прямых 3х—2у — 20 = 0, х + 6у— 20 = 0, при условии, что его оси со­впадают с осями координат.

---

497. Доказать, что произведение расстояний от центра эллипса до точки пересечения любой его касательной с фокальной осью и до основания перпендикуляра, опущенного из точки касания на фо­кальную ось, есть величина постоянная, равная квадрату большой полуоси эллипса.

498. Доказать, что произведение расстояний от фокусов до лю­бой касательной к эллипсу равно квадрату малой полуоси.

499. Прямая х—у— 5 = 0 касается эллипса, фокусы которого находятся в точках F₁ (—3; 0) и F₂ (3; 0). Составить уравнение этого эллипса.

500. Составить уравнение эллипса, фокусы которого располо­жены на оси абсцисс симметрично относительно начала координат, если известны уравнение касательной к эллипсу

3х+10у —25 = 0

и его малая полуось b = 2.

501. Доказать, что прямая, касающаяся эллипса в некоторой точке М, составляет равные углы с фокальными радиусами F₁M, F₂M и проходит вне угла F₁MF_2.

502. Из левого фокуса эллипса

под тупым углом  к оси Ох направлен луч света. Известно, что tg = — 2. Дойдя до эллипса, луч от него отразился. Составить уравнение прямой, на которой лежит отражённый луч.

503. Определить точки пересечения двух эллипсов:

х² + 9у² — 45 = 0, х² + 9у² —6х —27 = 0.

504. Убедившись, что два эллипса

n²m²+ m²y²— m²n² = 0, m²x² + n²y² — m²n² = 0 (mn)

пересекаются в четырёх точках, лежащих на окружности с центром в начале координат, определить радиус R этой окружности.

505. Две плоскости  и  образуют угол  = 30⁰. Определить полуоси эллипса, полученного проектированием на плоскость  окружности радиуса R =10, лежащей на плоскости .

506. Эллипс, малая полуось которого равна 6, является проек­цией окружности радиуса R=12. Определить угол  между пло­скостями, в которых лежат эллипс и окружность.

507. Направляющей круглого цилиндра является окружность радиуса R = 8. Определить полуоси эллипса, полученного в сечении этого цилиндра плоскостью, наклонённой к его оси под углом  = 30°.

508. Направляющей круглого цилиндра является окружность ра­диуса R = . Определить, под каким углом к оси цилиндра нужно его пересечь плоскостью, чтобы в сечении получить эллипс с большой полуосью а = 2.

---

509. Равномерным сжатием (или равномерным растяжением) плоскости к оси абсцисс называется такое преобразование точек

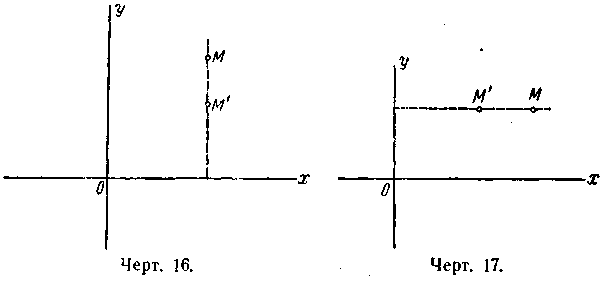
плоскости, при котором произвольная точка М(х; у) перемещается в точку М'(х'; у') (черт. 16) так, что

х' = х, у' = qy,

где q>0 — постоянная, называемая коэффициентом равномерного сжатия.

Аналогично определяется равномерное сжатие плоскости к оси Оу при помощи уравнений

x' = qx, y' = y (черт. 17).

Определить, в какую линию преобразуется окружность

х² + у² = 25,

если коэффициент равномерного сжатия плоскости к оси абсцисс

q = .

510. Коэффициент равномерного сжатия плоскости к оси Оуз равен 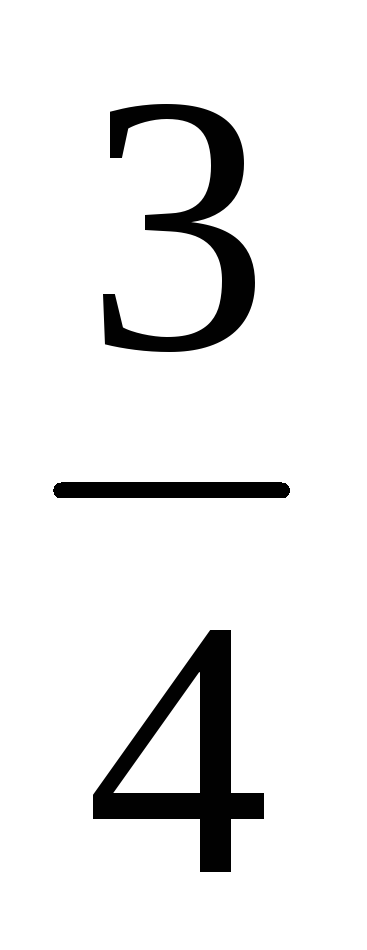. Определить уравнения линии, в которую при таком сжатии преобразуется эллипс

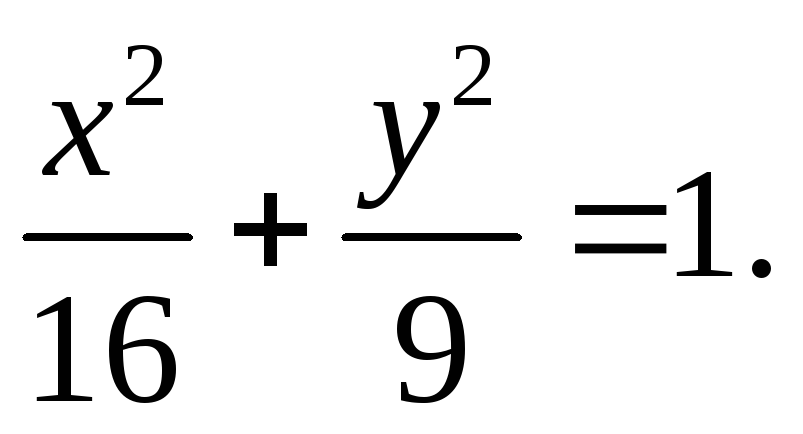
511. Найти уравнение линии, в которую преобразуется эллипс при двух последовательных равномерных сжатиях пло­скости к координатным осям, если коэффициенты равномерного сжатия плоскости к осям Ох и Оу равны соответственно и .

612. Определить коэффициент q равномерного сжатия плоскости к оси Ох, при котором эллипс преобразуется в эллипс .

613. Определить коэффициент q равномерного сжатия плоскости к оси Оу, при котором эллипс преобразуется в эллипс .

514. Определить коэффициенты q₁ и q₂ двух последовательных равномерных сжатий плоскости к осям Ох и Оу, при которых эллипс преобразуется в окружность х²+у²=16.

---

Смотрите также файлы

• kletenik_17.doc

• kletenik_16.doc

• kletenik_15.doc

• kletenik_14.doc

• kletenik_13.doc