§ 19. Гипербола

Гиперболой называется геометрическое место точек, для которых раз­ность расстояний от двух фиксированных точек плоскости, называемых фо­кусами, есть постоянная величина; указанная разность берётся по абсо­лютному значению и обозначается, обычно, через 2а. Фокусы гиперболы обозначают буквами F₁ и F₂ , расстояние между ними — через 2с. По опреде­лению гиперболы 2а < 2с, или а < с.

Пусть дана гипербола. Если оси декартовой прямоугольной системы координат выбраны так, что фокусы данной гиперболы располагаются на оси абсцисс симметрично относительно начала координат, то в этой системе координат уравнение гиперболы имеет вид

(1)

где b = . Уравнение вида (1) называется каноническим уравнением гиперболы. При указанном выборе системы координат оси координат являются

Черт. 18.

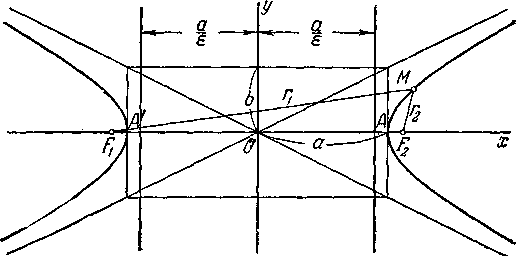
осями симметрии гиперболы, а начало координат — её центром симметрии (черт. 18). Оси симметрии гиперболы называются просто её осями, центр симметрии — центром гиперболы. Гипербола пересекает одну из своих осей; точки пересечения называются вершинами гиперболы. На черт. 18 вершины гиперболы суть точки А' и А.

Прямоугольник со сторонами 2а и 2b, расположенный симметрично от­носительно осей гиперболы и касающийся её в вершинах, называется основным прямоугольником гиперболы.

Отрезки длиной 2а и 2b, соединяющие середины сторон основного прямоугольника гиперболы, также называют её осями. Диагонали основного прямоугольника (неограниченно продолженные) являются асимптотами гипер­болы; их уравнения суть:

y = y = — Уравнение —

определяет гиперболу, симметричную относительно координатных осей с фо­кусами на оси ординат; уравнение (2), как и уравнение (1), называется кано­ническим уравнением гиперболы; в этом случае постоянная разность расстоя­ний от произвольной точки гиперболы до фокусов равна 2b. Две гиперболы, которые определяются уравнениями

---

—

в одной и той же системе координат, называются сопряжёнными.

Гипербола с равными полуосями (а = b) называется равносторонней; её каноническое уравнение имеет вид

х² — у² = а² или — х² — у² = а² .

Число , где а — расстояние от центра гиперболы до её вершины, называется эксцен­триситетом гиперболы. Очевидно, для любой гиперболы > 1. Если М (х; у)— произвольная точка гиперболы, то отрезки Р₁М и F₂ M (см. черт. 18) назы­ваются фокальными радиусами точки М. Фокальные радиусы точек правой ветви гиперболы вычисляются по формулам

r₁ = εx + a, r₂ = εx — a,

фокальные радиусы точек левой ветви — по формулам

r₁ = — εx + a, r₂ = — εx — a,

Если гипербола задана уравнением (1), то прямые, определяемые урав­нениями

x = x =

называются её директрисами (см. черт. 18). Если гипербола задана уравне­нием (2), то директрисы определяются уравнениями y = x =

Каждая директриса обладает следующим свойством: если r — расстояние от произвольной точки гиперболы до некоторого фокуса, d — расстояние от той же точки до односторонней с этим фокусом директрисы, то отношение есть постоянная величина, равная эксцентриситету гиперболы: =.

616. Составить уравнение гиперболы, фокусы которой располо­жены на оси абсцисс, симметрично относительно начала коорди­нат, зная, кроме того, что:

---

1) её оси 2а = 10 и 2b = 8;

2) расстояние между фокусами 2с =10 и ось 2b = 8;

3) расстояние между фокусами 2с = 6 и эксцентриситет ε =;

4) ось 2a = 16 и эксцентриситет ε =;

5) уравнения асимптот

y = ±

и расстояние между фокусами 2с — 20;

6) расстояние между директрисами равно 22 — и расстояние между фокусами 2с = 26;

7) расстояние между директрисами равно и ось 2b = 6;

8) расстояние между директрисами равно и эксцентриситет ε =;

9) уравнения асимптот у = ± и расстояние между директрисами равно 12 516. Составить уравнение гиперболы, фокусы которой располо­жены на оси ординат, симметрично относительно начала коорди­нат, зная, кроме того, что:

1) её полуоси а = 6, b = 18 (буквой а мы обозначаем полуось гиперболы, расположенную на оси абсцисс);

2) расстояние между фокусами 2с =10 и эксцентриситет

ε =;

3) уравнения асимптот

у = ±

и расстояние между вершинами равно 48;

4) расстояние между директрисами равно и эксцентриси­тет ε =;

5) уравнения асимптот у = ± и расстояние между директрисами равно .

517. Определить полуоси а и b каждой из следующих гипербол:

1) ^; 2) 3) х²— 4у² = 16;

---

4) х² —у² = 1; 5) 4х² — 9у² = 25; 6) 25х² — 16у² = 1;

7) 9х² —16у²=1.

518. Дана гипербола 16х² — 9у²=144. Найти: 1) полуоси а и b; 2) фокусы;

3) эксцентриситет; 4) уравнения асимптот; 5) урав­нения директрис.

619. Дана гипербола 16х² — 9у² = —144. Найти: 1) полуоси а и b; 2) фокусы; 3) эксцентриситет; 4) уравнения асимптот; 5) урав­нения директрис.

520. Вычислить площадь треугольника, образованного асимпто­тами гиперболы

и прямой

9х + 2у — 24 = 0.

521. Установить, какие линии определяются следующими урав­нениями:

1) y = + , 2) y = —3,

3) х = —, 4) у = + .

Изобразить эти линии на чертеже.

522. Дана точка М₁(10; — ) на гиперболе

.

Составить уравнения прямых, на которых лежат фокальные радиусы точки M₁.

523. Убедившись, что точка М₁(— 5; ) лежит на гиперболе

,

определить фокальные радиусы точки M₁.

524. Эксцентриситет гиперболы ε = 2, фокальный радиус ей точки М, проведённый из некоторого фокуса, равен 16. Вычислить расстояние от точки М до односторонней с этим фокусом дирек­трисы.

525. Эксцентриситет гиперболы ε = 3, расстояние от точки М гиперболы до директрисы равно 4. Вычислить расстояние от точки М до фокуса, одностороннего с этой директрисой.

526. Эксцентриситет гиперболы ε = 2, центр её лежит в начале координат, один из фокусов F(12; 0). Вычислить расстояние от точки М₁ гиперболы с абсциссой, равной 13, до директрисы, соответствующей заданному фокусу.

---

527. Эксцентриситет гиперболы ε = , центр её лежит в начале координат, одна из директрис дана уравнением х = — 8. Вычи­слить расстояние от точки М₁ гиперболы с абсциссой, равной 10, до фокуса, соответствующего заданной директрисе.

528. Определить точки гиперболы , расстояние которых до правого фокуса равно 4,5.

529. Определить точки гиперболы , расстояние кото­рых до левого фокуса равно 7.

530. Через левый фокус гиперболы проведён пер­пендикуляр к её оси, содержащей вершины. Определить расстояния от фокусов до точек пересечения этого перпендикуляра с гипер­болой.

531. Пользуясь одним циркулем, построить фокусы гиперболы (считая, что оси координат изображены и масштабная единица задана).

532. Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны:

1) точки M₁(6; —1) и М₂(—8; 2 ) гиперболы;

2) точка M₁(— 5; 3) гиперболы и эксцентриситет ε = ;

3) точка M₁(; —1) гиперболы и уравнения асимптот y = ;

4) точка M₁(—3; ) гиперболы и уравнения директрис y = ;

5) уравнения асимптот у =  и уравнения директрис x = ;

533. Определить эксцентриситет равносторонней гиперболы.

534. Определить эксцентриситет гиперболы, если отрезок между её вершинами виден из фокусов сопряжённой гиперболы под углом в 60°.

535. Фокусы гиперболы совпадают с фокусами эллипса

---

Смотрите также файлы

• kletenik_18.doc

• kletenik_17.doc

• kletenik_16.doc

• kletenik_15.doc

• kletenik_14.doc