§ 20. Парабола

Параболой называется геометрическое место точек, для каждой из кото­рых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называе­мой директрисой. Фокус параболы обозначается буквой F, расстояние от фокуса до директрисы — буквой р. Число р называется параметром параболы.

Пусть дана некоторая парабола. Введём декартову прямоугольную си­стему координат так, чтобы ось абсцисс проходила через фокус данной параболы перпендикулярно к директрисе и была направлена от директрисы к фокусу; начало координат расположим посредине между фокусом и дире­ктрисой (черт. 19). В этой системе координат данная парабола будет опреде­ляться уравнением

Y² = 2рх. (1)

Уравнение (1) называется каноническим уравнением параболы. В этой же системе координат директриса данной параболы имеет уравнение

х = — .

Фокальный радиус произвольной точки М(х; у) параболы (т. е. длина от­резка FM) может быть вычислен по формуле

r = x +

Парабола имеет одну ось симметрии, называемую осью параболы, с ко­торой она пересекается в единственной точке. Точка пересечения параболы

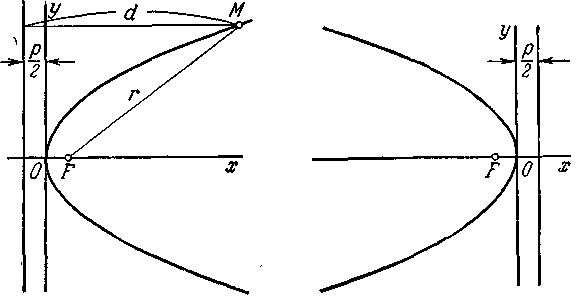
Черт. 19. Черт. 20.

с осью называется её вершиной. При указанном выше выборе координатной системы ось параболы совмещена с осью абсцисс, вершина находится в на­чале координат, вся парабола лежит в правой полуплоскости.

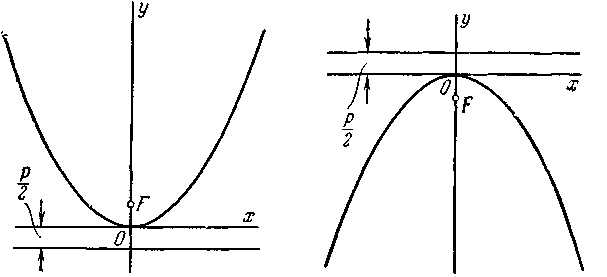
Черт. 21. Черт. 22.

Если координатная система выбрана так, что ось абсцисс совмещена с осью параболы, начало координат — с вершиной, но парабола лежит в ле­вой полуплоскости (черт. 20), то её уравнение будет иметь вид

y² = —2рx. (2)

В случае, когда начало координат находится в вершине, а с осью сов­мещена ось ординат, парабола будет иметь уравнение

x² = 2ру, (3)

если она лежит в верхней полуплоскости (черт. 21), и

х² = —2ру (4)

— если в нижней полуплоскости (черт. 22).

---

Каждое из уравнений параболы (2), (3), (4), как и уравнение (1), назы­вается каноническим.

583. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола расположена в правой полуплоскости, симметрично относительно оси Ох, и её параметр р = 3;

2) парабола расположена в левой полуплоскости, симметрично относительно оси Ох, и её параметр р = 0,5;

3) парабола расположена в верхней полуплоскости, симметрично относительно оси Оу, и её параметр p = ;

4) парабола расположена в нижней полуплоскости, симметрично относительно оси Оу, и её параметр р =3.

584. Определить величину параметра и расположение относи­тельно координатных осей следующих парабол:

1) у² = 6х; 2) х² = 5у; 3) у² = — 4х; 4) х² = — у.

585. Составить уравнение параболы, вершина которой находится в начале координат, зная, что:

1) парабола симметрично расположена относительно оси Ох и проходит через точку А (9; 6);

2) парабола симметрично расположена относительно оси Ох и проходит через точку В(—1; 3);

3) парабола симметрично расположена относительно оси Оу и проходит через точку С(1; 1);

4) парабола симметрично расположена относительно оси Оу и проходит через точку D (4; — 8).

586. Стальной трос подвешен за два конца; точки крепления расположены на одинаковой высоте; расстояние между ними равно 20 м. Величина его прогиба на расстоянии 2 м от точки крепления, считая по горизонтали, равна 14,4 см. Определить величину прогиба этого троса в середине между точками крепления, приближённо считая, что трос имеет форму дуги параболы.

587. Составить уравнение параболы, которая имеет фокус F(0; —3) и проходит через начало координат, зная, что её осью служит ось Оу.

588. Установить, какие линии определяются следующими урав­нениями:

1) у = + 2, 2) у = +, 3) у = — 3,

4) у = — 2, 5) х = + , 6) х = — 5,

---

7) х = — , 8) х = + 4.

Изобразить эти линии на чертеже.

589. Найти фокус F и уравнение директрисы параболы у² = 24х.

590. Вычислить фокальный радиус точки М параболы у² = 20х, если абсцисса точки М равна 7.

591. Вычислить фокальный радиус точки М параболы у²=12х, если ордината точки М равна 6.

592. На параболе у^а=16х найти точки, фокальный радиус которых равен 13.

593. Составить уравнение параболы, если дан фокус F(— 7; 0) и уравнение директрисы х—7 = 0.

594. Составить уравнение параболы, зная, что её вершина совпа­дает с точкой (а; 3), параметр равен р, ось параллельна оси Ох и парабола простирается в бесконечность:

1) в положительном направлении оси Ох;

2) в отрицательном направлении оси Ох.

595. Составить уравнение параболы, зная, что её вершина совпа­дает с точкой (а; (3), параметр равен р, ось параллельна оси Оу и парабола простирается в бесконечность:

1) в положительном направлении оси Оу (т. е. парабола является восходящей);

2) в отрицательном направлении оси Оу (т. е. парабола является нисходящей).

596. Установить, что каждое из следующих уравнений определяет параболу, и найти координаты её вершины А, величину параметра р и уравнение директрисы:

1) у² = 4х — 8, 2) у² = 4 — 6х,

3) х² = 6у + 2, 4) х² = 2— у.

597. Установить, что каждое из следующих уравнений опреде­ляет параболу, и найти координаты её вершины А и величину параметра р:

1) y = х² + х + 2, 2) y = 4x² — 8x + 7,

3) y = — х² + 2х— 7.

698. Установить, что каждое из следующих уравнений опреде­ляет параболу, и найти координаты её вершины А и величину параметра р:

1) х = 2у² — 12у + 14, 2) х = — у² + у,

3) х = — у² + 2у — 1.

599. Установить, какие линии определяются следующими уравне­ниями:

---

1) у = 3 — 4, 2) х = — 4 + 3,

3) х = 2 — , 4) у = — 5 — .

Изобразить эти линии на чертеже.

600. Составить уравнение параболы, если даны её фокус F(7; 2) и директриса х — 5 = 0.

601. Составить уравнение параболы, если даны её фокус F(4; 3) и директриса у + 1 = 0.

602. Составить уравнение параболы, если даны её фокус F(2; —1) и директриса х — у — 1 = 0.

603. Дана вершина параболы А (6; —3) и уравнение ее дире­ктрисы

3х —5у + 1 = 0.

Найти фокус F этой параболы.

604. Дана вершина параболы А(—2; —1) и уравнение её ди­ректрисы

х + 2у — 1 = 0.

Составить уравнение этой параболы.

605. Определить точки пересечения прямой х + у— 3 = 0, и параболы х² = 4у.

606. Определить точки пересечения прямой 3х + 4у—12 = 0 и параболы у² = — 9х.

607. Определить точки пересечения прямой 3х — 2у + 6 = 0 и параболы у² = 6х.

608. В следующих случаях определить, как расположена данная прямая относительно данной параболы — пересекает ли, касается или проходит вне её:

1) х—у + 2 = 0, у² = 8х;

2) 8х + 3у—15 = 0, х² = —3у;

3) 5х—у—15 = 0, у² = —5х.

609. Определить, при каких значениях углового коэффициента k

прямая у = Ах + 2:

1) пересекает параболу у² = 4х;

2) касается её;

3) проходит вне этой параболы.

610. Вывести условие, при котором прямая y = kx + b касается параболы у² = 2рх.

611. Доказать, что к параболе у² = 2рх можно провести одну и только одну касательную с угловым коэф­фициентом k ≠ 0.

612. Составить уравнение касательной к параболе у² = 2рх в её точке М₁(х₁; у₁)

613. Составить уравнение прямой, которая касается пара­болы у² = 8х и параллельна прямой

2х + 2у —3 = 0.

614. Составить уравнение прямой, которая касается пара­болы х²=16у и перпендикулярна к прямой

2х+4у + 7 = 0.

---

615. Провести касательную к параболе у²=12х параллельно прямой

3х — 2у + 30 = 0

и вычислить расстояние d между этой касательной и данной прямой.

616. На параболе у² = 64х найти точку М₁ ближайшую к прямой

4х+3у—14 = 0,

и вычислить расстояние d от точки М₁ до этой прямой.

617. Составить уравнения касательных к параболе у² = 36х, проведённых из точки А (2; 9).

618. К параболе у² = 2рх проведена касательная. Доказать, что вершина этой параболы лежит посредине между точкой пересечения касательной с осью Ох и проекцией точки касания на ось Ох.

619. Из точки А (5; 9) проведены касательные к параболе y² = 5х. Составить уравнение хорды, соединяющей точки касания.

620. Из точки Р(—3; 12) проведены касательные к параболе

у²=10х.

Вычислить расстояние d от точки Р до хорды параболы, соеди­няющей точки касания.

621. Определить точки пересечения эллипса па­раболы у² = 24х.

622. Определить точки пересечения гиперболы

и параболы у² = 3х.

623. Определить точки пересечения двух парабол:

у = х² — 2х+1, х = у² —6у + 7.

624. Доказать, что прямая, касающаяся параболы в некоторой точке М, составляет равные углы с фокальным радиусом точки М и с лучом, который, исходя из М, идёт параллельно оси параболы в ту сторону, куда парабола бесконечно простирается.

625. Из фокуса параболы

у²=12х

под острым углом а к оси Ох направлен луч света. Известно, что 3 tgα = . Дойдя до параболы, луч от неё отразился. Составить

уравнение прямой, на которой лежит отражённый луч.

626. Доказать, что две параболы, имеющие общую ось и общий фокус, расположенный между их вершинами, пересекаются под пря­мым углом.

627. Доказать, что если две параболы со взаимно перпендику­лярными осями пересекаются в четырёх точках, то эти точки лежат на одной окружности.

---

Смотрите также файлы

• kletenik_19.doc

• kletenik_18.doc

• kletenik_17.doc

• kletenik_16.doc

• kletenik_15.doc