§ 23. Центр линии второго порядка

Линия, которая в некоторой декартовой системе координат определяется уравнением второй степени, называется линией второго порядка. Общее уравнение второй степени (с двумя переменными) принято записывать в виде:

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0. (1),

Центром некоторой линии называется такая точка плоскости, по отно­шению к которой точки этой линии расположены симметрично парами. Ли­нии второго порядка, обладающие единственным центром, называются цен­тральными.

Точка S (х₀; у_а) является центром линии, определяемой уравнением (1) в том и только в том случае, когда её координаты удовлетворяют уравне­ниям:

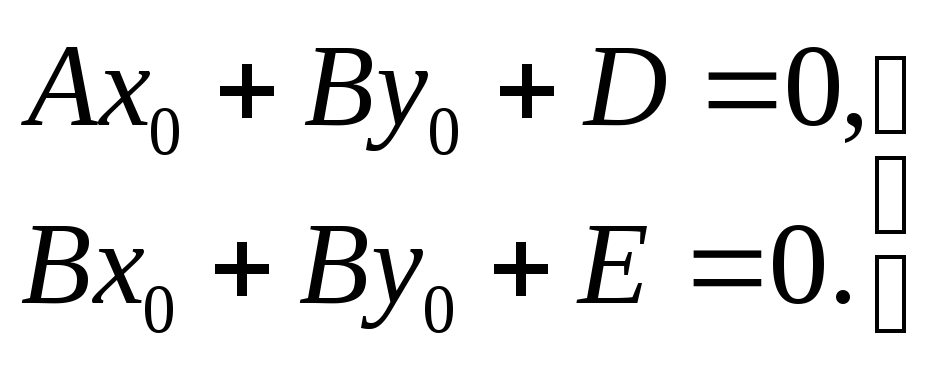(2)

Обозначим через определитель этой системы:

.

Величина составляется из коэффициентов при старших членах уравне­ния (1) и называется дискриминантом старших членов этого уравнения.

Если  0, то система (2) является совместной и определённой, т. е. имеет решение и притом единственное. В этом случае координаты центра могут быть определены по формулам:



Неравенство 0 служит признаком центральной линии второго порядка.

Если S (х₀ , у₀) — центр линии второго порядка, то в результате преобра­зования координат по формулам

(что соответствует переносу начала координат в центр линии) её уравнение примет вид

,

---

где А, В, С — те же, что в данном уравнении (1), а определяется форму­лой

В случае  0 имеет место также следующая формула:

где

.

Определитель  называется дискриминантом левой части общего уравнения второй степени.

665. Установить, какие из следующих линий являются централь­ными (т. е. имеют единственный центр), какие не имеют центра, какие имеют бесконечно много центров:

1) 3х² — 4ху — 2у² + 3х — 12у — 7 = 0;

2) 4х² + 5ху + 3y² — х + 9у — 12 = 0;

3) 4х² — 4ху +y² — 6х + 8у + 13 = 0;

4) 4х² — 4ху + y² — 12х + 6у — 11 = 0;

5) х² — 2ху + 4у² + 5х —7у+12=0;

6) х² — 2ху + у² — 6х + 6у — 3 = 0;

7) 4х² — 20ху + 25у² — 14х + 2у — 15 = 0;

8) 4х² — 6ху — 9у² + 3х — 7у + 12 = 0.

666. Установить, что следующие линии являются центральными, и для каждой из них найти координаты центра:

1) 3х² + 5ху +y² — 8х — 11у — 7 = 0;

2) 5х² + 4ху + 2y² + 20х+ 20у — 18 = 0;

3) 9х² — 4ху — 7y² — 12 = 0;

4) 2х² — 6ху + 5у² + 22х — 36у + 11 = 0.

667. Установить, что каждая из следующих линий имеет беско­нечно много центров; для каждой из них составить уравнение гео­метрического места центров:

1) х² — 6ху + 9y² — 12х + 36y + 20 = 0;

2) 4х² + 4ху + у² — 8х — 4у — 21 = 0;

3) 25x² — 10ху + у² + 40х — 8у + 7 = 0.

668. Установить, что следующие уравнения определяют централь­ные линии; преобразовать каждое из них путём переноса начала координат в центр:

---

1) 3х² — 6ху + 2у² — 4х + 2у+1=0;

2) 6х² + 4ху +y² + 4х — 2у + 2=0;

3) 4х² + 6ху+у² — 10х —10 = 0;

4) 4х² + 2ху + 6y² + 6х — 10у + 9 = 0.

669. При каких значениях т и п уравнение

mх² + 12ху + 9у² + 4х + пу — 13 = 0

определяет:

а) центральную линию;

б) линию без центра;

в) линию, имеющую бесконечно много центров.

670. Дано уравнение линии 4х² — 4ху +у² + 6х + 1 =0.

Определить, при каких значениях углового коэффициента k прямая

у = kx

а) пересекает эту линию в одной точке;

б) касается этой линии;

в) пересекает эту линию в двух точках;

г) не имеет общих точек с этой линией.

671. Составить уравнение линии второго порядка, которая, имея центр в начале координат, проходит через точку М (6; —2) и касается прямой

х —2 = 0

в точке N (2; 0).

672. Точка Р (1; —2) является центром линии второго порядка, которая проходит через точку Q (0;—3) и касается оси Ох в начале координат. Составить уравнение этой линии.

---

Смотрите также файлы

• kletenik_22.doc

• kletenik_21.doc

• kletenik_20.doc

• kletenik_19.doc

• kletenik_18.doc