§ 25. Приведение к простейшему виду

параболического уравнения

Пусть уравнение

(1)

является параболическим, т. е. удовлетворяет условию

.

В этом случае линия, определяемая уравнением (1), либо не имеет центра, либо имеет бесконечно много центров. Упрощение параболического уравне­ния целесообразно начать с поворота координатных осей, т. е. сначала преобразовать уравнение (1) при помощи формул

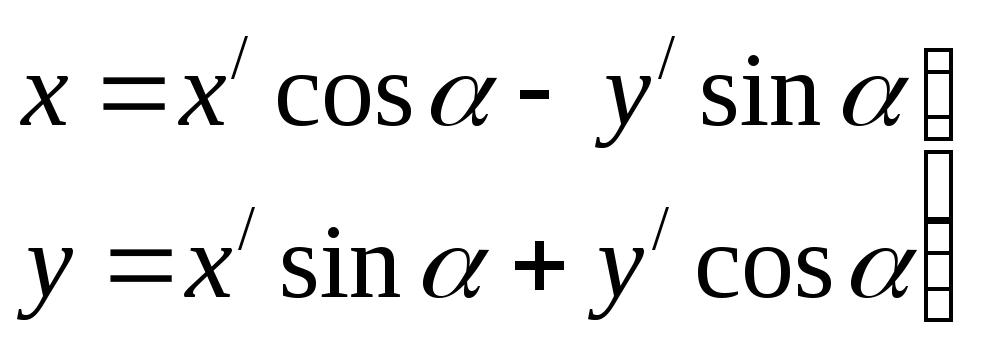(2)

Угол следует найти из уравнения

(3)

тогда в новых координатах уравнение (1) приводится либо к виду

, (4)

где , либо к виду

(5)

где .

Дальнейшее упрощение уравнений (4) и (5) достигается путём параллель­ного перенесения (повёрнутых) осей.

689. Установить, что каждое из следующих уравнений является параболическим; каждое из них привести к простейшему виду; установить, какие геометрические образы они определяют; для каж­дого случая изобразить на чертеже оси первоначальной координат­ной системы, оси других координатных систем, которые вводятся по ходу решения, и геометрический образ, определяемый данным уравнением:

1) 9х² —24ху+16у² —20х+110у —50 = 0;

2) 9х² + 12ху + 4у² — 24х — 16у + 3 = 0;

3) 16х² — 24ху + 9у^а — 160х+ 120у + 425 = 0.

690. То же задание, что и в предыдущей задаче, выполнить для уравнений:

1) 9х² + 24ху+16у²—18х + 226у +209 = 0;

2) х² — 2ху+у² — 12х+12у— 14 = 0;

---

3) 4х² + 12ху + 9у² —4х —6у+1=0.

691. Для любого параболического уравнения доказать, что коэффициенты А и С не могут быть числами разных знаков и что они одновременно не могут обращаться в нуль.

692. Доказать, что любое параболическое уравнение может быть написано в виде:

Доказать также, что эллиптические и гиперболические уравне­ния в таком виде не могут быть написаны.

693. Установить, что следующие уравнения являются параболи­ческими, и записать каждое из них в виде, указанном в задаче 692:

1) х² + 4ху + 4у² + 4х+у—15 = 0;

2) 9х² —6ху+у² —х + 2у—14 = 0;

3) 25х² — 20ху + 4у² + 3х —у +11=0;

4) 16х²+16ху + 4у² — 5х + 7у = 0;

5) 9х² — 42ху + 49у² + 3х — 2у — 24 = 0.

694. Доказать, что если уравнение второй степени является параболическим и написано в виде

то дискриминант его левой части определяется формулой

.

695. Доказать, что параболическое уравнение

при помощи преобразования

приводится к виду

где

а — дискриминант левой части данного уравнения.

696. Доказать, что параболическое уравнение определяет пара­болу в том и только в том случае, когда . Доказать, что в этом случае параметр параболы определяется формулой

---

697. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет параболу, и найти параметр этой параболы:

1) 9х² + 24ху+16у² — 120х + 90у = 0;

2) 9х² — 24ху+16у² — 54х—178у+181=0;

3) х² —2ху+у² + 6х—14у + 29 = 0;

4) 9х² — 6ху +у² — 50х + 50у — 275 = 0.

698. Доказать, что уравнение второй степени является уравне­нием вырожденной линии в том и только в том случае, когда = 0.

699. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет пару параллельных прямых, и найти их уравнения:

а) 4х² + 4ху+у² —12х —6у + 5 = 0;

б) 4х² — 12ху + 9у² + 20х — 30у — 11 = 0;

в) 25х² — 10xу +у² + 10х — 2у —15 = 0.

700. Не проводя преобразования координат, установить, что каждое из следующих уравнений определяет одну прямую (пару слившихся прямых), и найти уравнение этой прямой:

а) х² —6ху + 9у² + 4х—12у + 4 = 0;

б) 9х² + 30ху + 25у² + 42х + 70у + 49 = 0;

в) 16х²—16ху+4у² —72х+36у + 81=0.

---

Смотрите также файлы

• kletenik_24.doc

• kletenik_23.doc

• kletenik_22.doc

• kletenik_21.doc

• kletenik_20.doc