§ 26. Уравнения некоторых кривых, встречающихся

в математике и её приложениях

701. Составить уравнение геометрического места точек, произ­ведение расстояний которых до двух данных точек F₁ (— с; 0) и

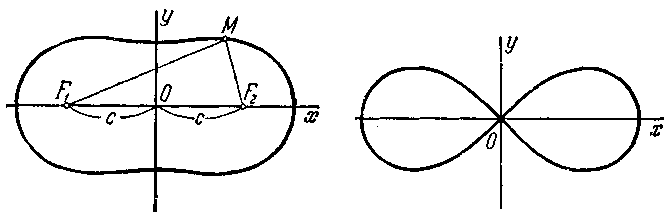
Черт. 23. Черт. 24.

F₂ (с; 0) есть постоянная величина а². Такое геометрическое место точек называется о в а л о м К а с с и н и (черт. 23).

702. Составить уравнение геометрического места точек, про-. изведение расстояний которых до двух данных точек F₁ (— а; 0) и F₂ (а; 0) есть постоянная величина а². Такое геометрическое место точек называется л е м н и с к а т о й (черт. 24). (Уравнение лемнискаты сначала найти непосредственно, потом — рассматривая её как частный вид овала Кассини.) Составить также уравнение лемнискаты в полярных координатах, совмещая полярную ось с поло­жительной полуосью Ох и полюс с началом координат.

703. Составить уравнение геометрического места оснований пер­пендикуляров, опущенных из начала координат на прямые, отсе­кающие от координатного угла треугольники постоянной площади S.

У к а з а н и е. Составить уравнение сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох.

704. Доказать, что геометрическое место точек задачи 703 есть лемниската (см. задачу 702).

У к а з а н и е. Повернуть координатные оси на угол в 45°.

705. Луч а, в начальном положении совпадающий с полярной осью, вращается вокруг полюса О с постоянной угловой ско­ростью ω. Составить в данной системе полярных координат уравне­ние траектории точки М, которая, имея начальное положение в О, движется по лучу а равномерно со скоростью v (спираль Архи­меда, черт. 25).

706. Дана прямая х=2r и окружность радиуса r, которая про­ходит через начало координат О и касается данной прямой. Из точки О проведен луч, пересекающий данную окружность в точке В и данную прямую в точке С, на котором отложен отрезок

О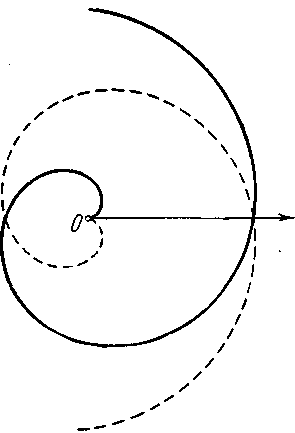М = ВС (черт. 26). При вра­щении луча длина отрезка ОМ меняется и точка М описывает кривую, называемую ц и с с о и д о й. Составить уравнение циссоиды.

---

707. Дана прямая х = а (а > 0) и окружность диаметра а, прохо­дящая через начало координат О, и касающаяся данной прямой. Из точки О проведён луч, пересекаю­щий окружность в точке А и дан­ную прямую в точке В. Из точек А и В проведены прямые, парал­лельные соответственно осям Оу и Ох (черт. 27). Точка М пересе­чения этих прямых при вращении луча описывает кривую, называемую в е р з ь е р о й. Составить её урав­нение.

708. Из точки А (— а; 0), где a > 0, проведён луч АВ (черт. 28), на котором по обе стороны от

Черт. 25. точки В отложены отрезки ВМ и BN одинаковой длины b (b = const.). При вращении луча точки М к N описывают кривую, назы­ваемую конхоидой. Составить её уравнение сначала в полярных координатах, помещая полюс в точку А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.

709. Из точки А(—а; 0), где a > 0, проведён луч АВ (черт. 29), на котором по обе стороны от точки В отложены отрезки ВМ и BN, равные 0В. При вращении луча точки М и N описы­вают кривую, называемую с т р о ф о и д о й. Составить её урав­нение сначала в полярных координатах, помещая полюс в точке А и направляя полярную ось в положительном направлении оси Ох, а затем перейти к данной системе декартовых прямоугольных координат.

710. Из начала координат проведён луч, пересекающий данную окружность x2 + y² = 2ax (а > 0) в точке В (черт. 30); на луче

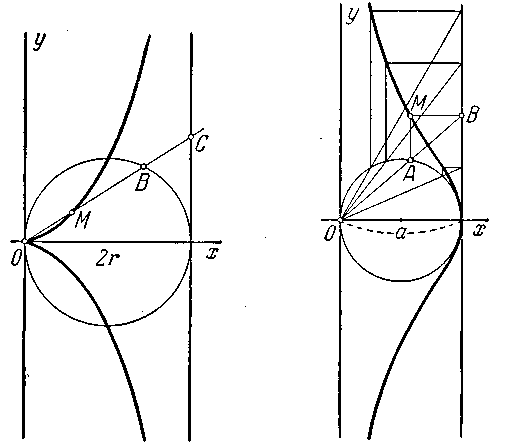
Черт. 26. Черт. 27.

по обе стороны от точки В отложены равные между собой отрезки ВМ и BN постоянной длины b, При вращении луча точки М и N

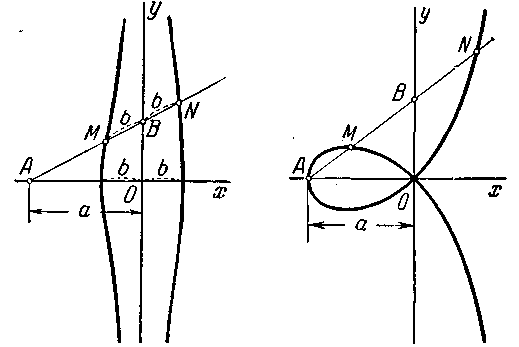
Черт. 28. Черт. 29.

описывают кривую, называемую у л и т к о й П а с к а л я (черт. 30). Составить её уравнение сначала в полярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых

прямоугольных координат.

7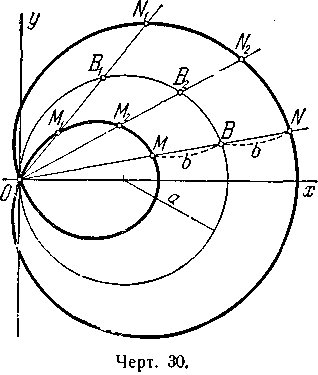11. Отрезок длины 2а движется так, что его концы всё время находятся на координатных осях. Составить уравнение траектории основания М перпендикуляра, опущенного из начала коорди­нат на отрезок (черт. 31), сна­чала в полярных координатах, совмещая полюс с началом ко­ординат и полярную ось с поло­жительной полуосью Ох, а затем перейти к данной си­стеме декартовых прямоуголь­ных координат. Точка М описывает кривую, называемую четырёхлепестковой розой.

---

7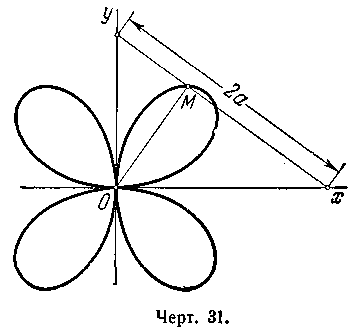12. Отрезок длины а дви­жется так, что его концы всё время находятся на коорди­натных осях (черт. 32). Через концы отрезка проведены пря­мые, параллельные координат­ным осям, до их взаимного пересечения в точке Р. Соста­вить уравнение траектории основания М перпендикуляра, опущенного из точки Р на от­резок. Эта траектория назы­вается а с т р о и д о й.

У к а з а н и е. Составить сна­чала параметрические уравнения астроиды, выбирая параметр t, как указано на черт. 32 (затем исклю­чить параметр t).

713. Из точки В пересече­ния луча ОВ с окружностью х²+у² = ах опущен перпен­дикуляр ВС на ось Ох. Из точки С на луч ОВ опущен перпенди­куляр СМ. Вывести уравнение траектории точки М сначала в по­лярных координатах, совмещая полюс с началом координат и полярную ось с положительной полуосью Ох, а затем перейти к данной системе декартовых прямоугольных координат.

714. Нить, намотанная на окружность х² + у² = а², разматы­вается так, что в точке В, где нить отделяется от окружности, она

остаётся касательной к ней (черт. 33). Найти параметрические уравнения линии, описываемой концом нити, если начальным положе­нием конца является точка А (а; 0), где a > 0. Линия, о которой идёт речь, называется э в о л ь в е н т о й к р у г а.

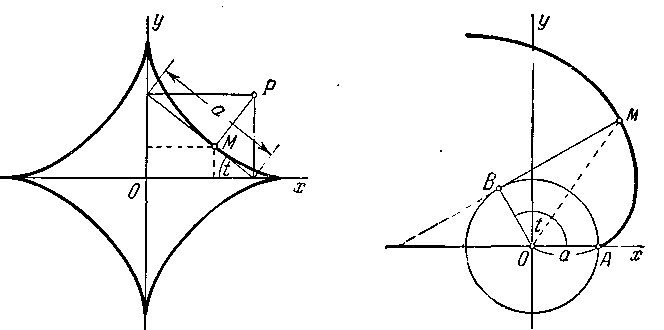
Черт. 32. Черт. 33.

7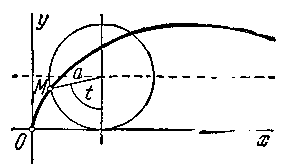15. Круг радиуса а катится без скольжения по оси Ох. Траек­тория некоторой точки М окружности этого круга называется циклоидой (черт. 34). Вывести параметрические уравнения циклоиды, принимая в качестве параметра t угол, на который по­ворачивается катящаяся окружность вокруг своего центра; считать при этом, что в начальный момент (t = 0) точка М находится в начале коор­динат. Исключить параметр t из полу­ченных уравнений.

716. Круг радиуса а катится без скольжения по окружности х² +у²=а², оставаясь вне её. Траектория некоторой точки M окружности Черт. 34.

катяще­гося круга называется к а р д и о и д о й (черт. 35). Вывести параме­трические уравнения кардиоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведён­ного в точку касания с подвижной. Считать при этом, что в на­чальный момент (t = Q) точка М находится справа на оси Ох. Перейти к полярным координатам при условии, что направление полярной оси совпадает с положительным направлением оси абсцисс, а полюс находится в точке А.

---

Доказать, что кардиоида есть частный вид улитки Паскаля (см. задачу 710).

717. Круг радиуса а катится без скольжения по окружности х² + у² = b², оставаясь вне её. Траектория некоторой точки М окружности катящегося круга называется эпициклоидой

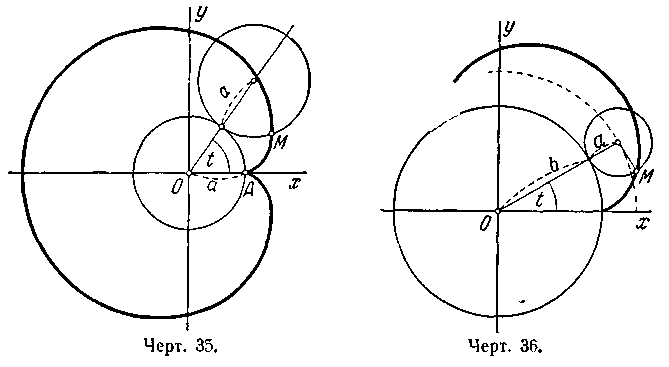
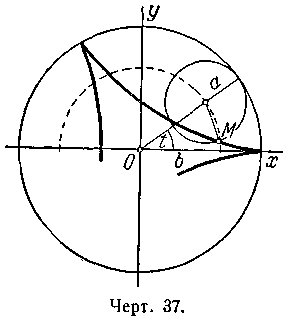(черт. 36). Вывести параметрические уравнения эпициклоиды, выби­рая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведённого в точку касания с подвижной; счи­тать при этом, что в начальный мо­мент (t = 0) точка М находится справа на оси Ох. Доказать, что кардиоида (см. задачу 716) есть частный вид эпициклоиды.

718. Круг радиуса а катит­ся без скольжения по окружно­сти х² + у² = b², оставаясь внутри неё. Траектория некоторой точ­ки М окружности катящегося кру­га называется гипоциклоидой (черт. 37). Вывести параметрические уравнения гипоциклоиды, выбирая в качестве параметра t угол наклона к оси Ох радиуса неподвижной окружности, проведённого в точку касания с подвижной; считать при этом, что в начальный момент (t = 0) точка М находится справа на оси Ох, Доказать, что аст­роида (см. задачу 712) есть частный вид гипоциклоиды.

---

Смотрите также файлы

• kletenik_25.doc

• kletenik_24.doc

• kletenik_23.doc

• kletenik_22.doc

• kletenik_21.doc