ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.07.2024
Просмотров: 22
Скачиваний: 0
§ 5. Решение и исследование системы трёх уравнений первой
степени с тремя неизвестными
Рассмотрим систему уравнений
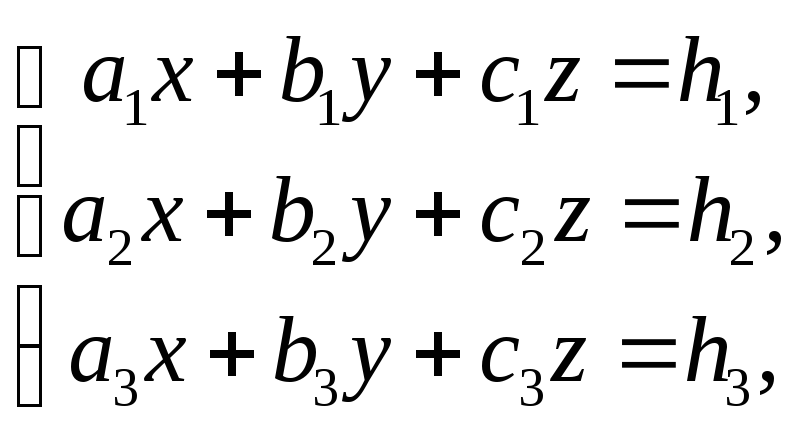 (1)
(1)
с неизвестными х, у, z (коэффициенты at, b1 ..., с2 и свободные члены h1, h2, h3 предположим данными).
Введём обозначения:
=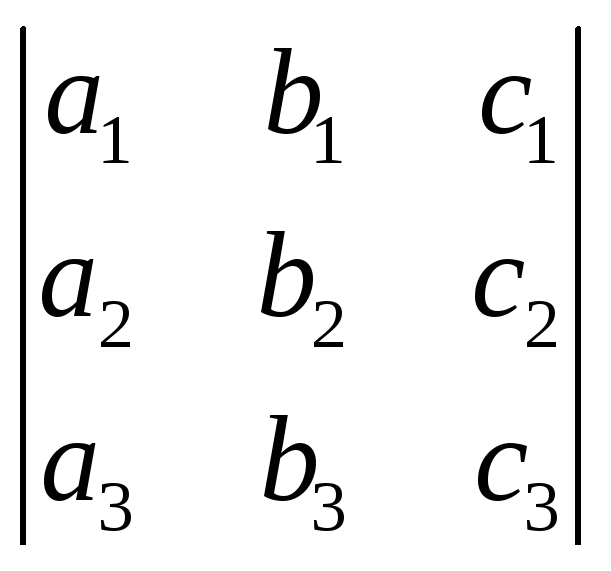 ,
=
,
=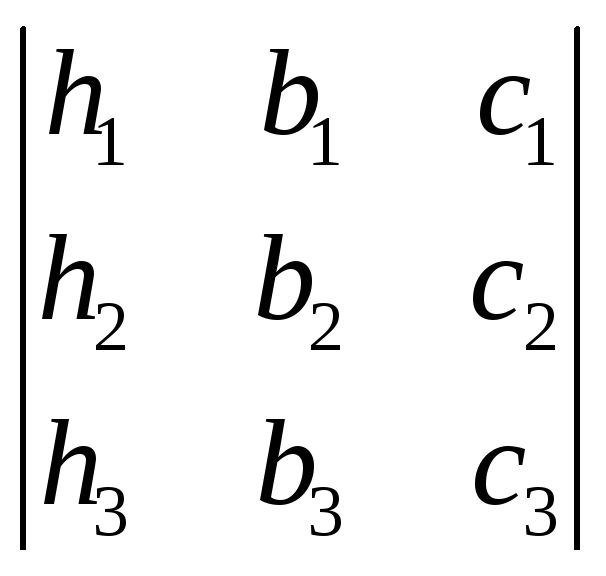 ,
=
,
=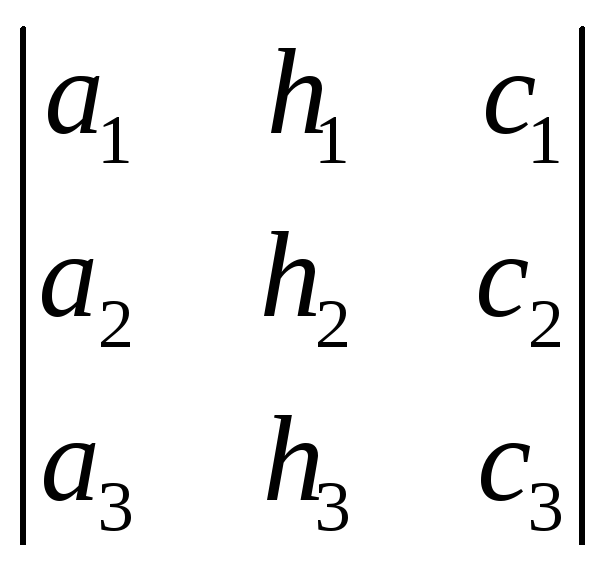 ,
=
,
= .
.
Определитель , составленный из коэффициентов при неизвестных системы (1), называется определителем данной системы.
Полезно заметить, что определители x, y, z получаются из определителя при помощи замены соответственно его первого, второго и, наконец, третьего столбца — столбцом свободных членов данной системы. Если 0, то система (1) имеет единственное решение; оно определяется формулами
x
=
![]() y =
y =
![]() z =
z =
![]()
Предположим теперь, что определитель системы равен нулю: = 0. Если в случае = 0 хотя бы один из определителей x, y, z отличен от нуля, то система (1) совсем не имеет решений.
В случае, когда = 0 и одновременно 1 = 0, 2 = 0, 3 = 0, система (1) также может совсем не иметь решений; но если система (1) при этих условиях имеет хотя бы одно решение, то она имеет бесконечно много различных решений. Однородной системой трёх уравнений первой степени с тремя неизвестными называется система вида:
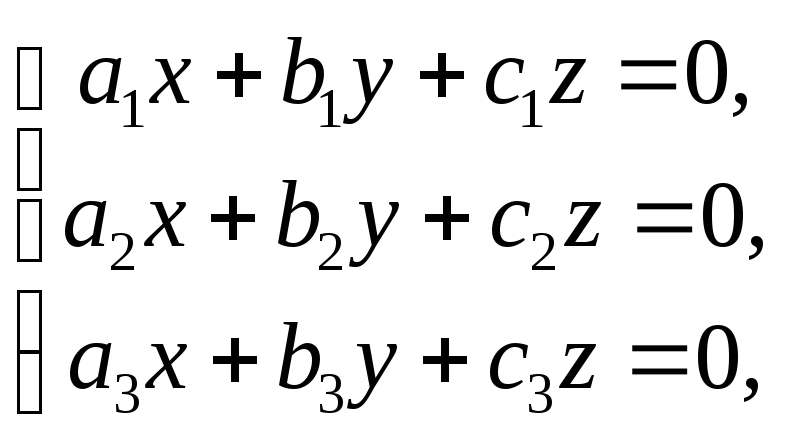
т. е. система уравнений, свободные члены которых равны нулю. Очевидно, что такая система всегда имеет решение: x = 0, у = 0, z = 0; оно называется нулевым. Если 0, то это решение является единственным. Если же = 0, то однородная система (2) имеет бесконечно много ненулевых решений.
В задачах 1236—1243 требуется установить, что системы уравнений имеют единственное решение, и найти его.
1236.
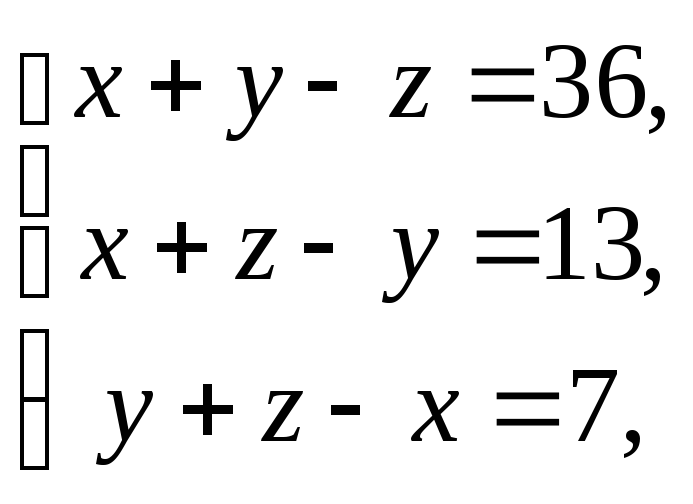 1237.
1237.
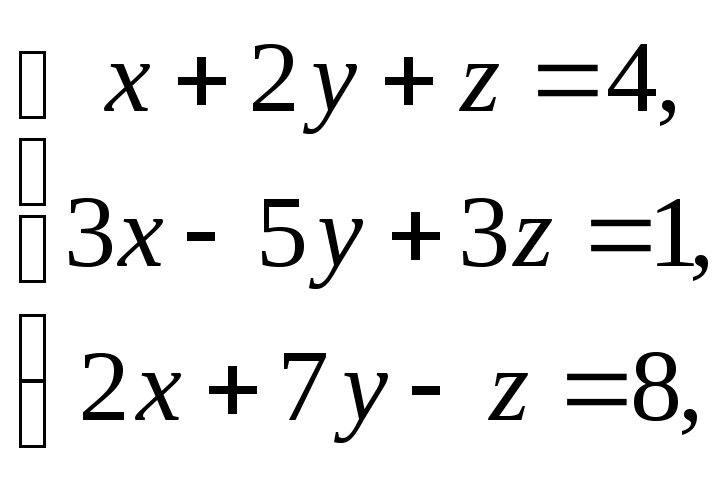
1238.
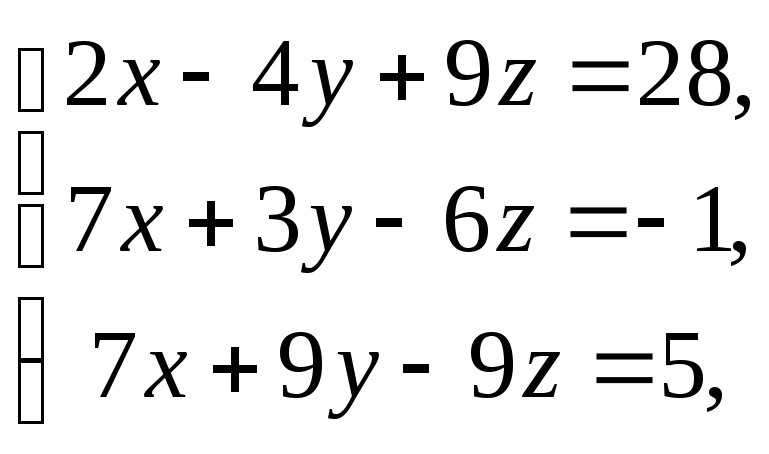 1239.
1239.
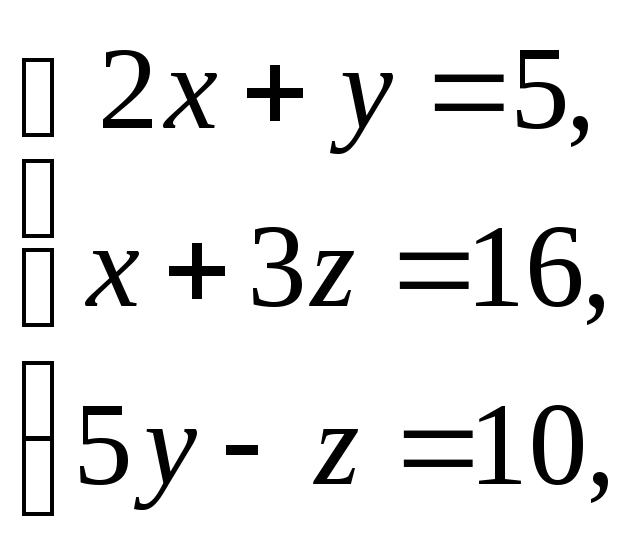
1240.
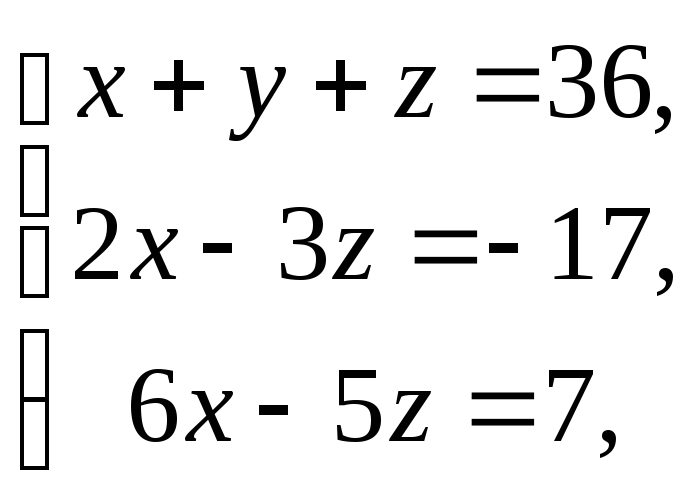 1241.
1241.
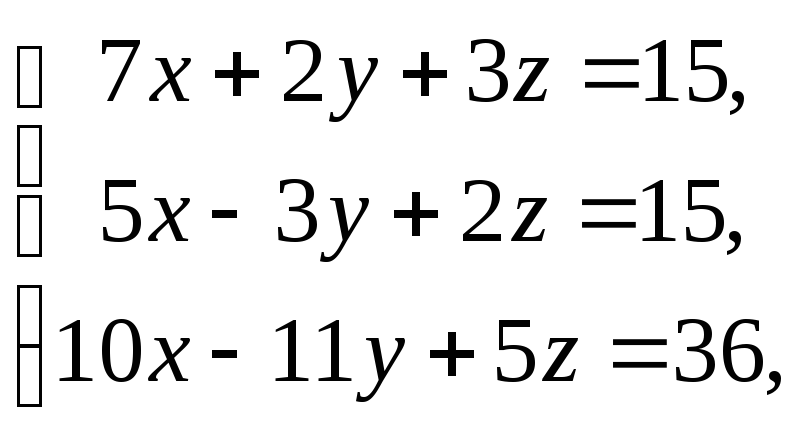 1242.
1242.
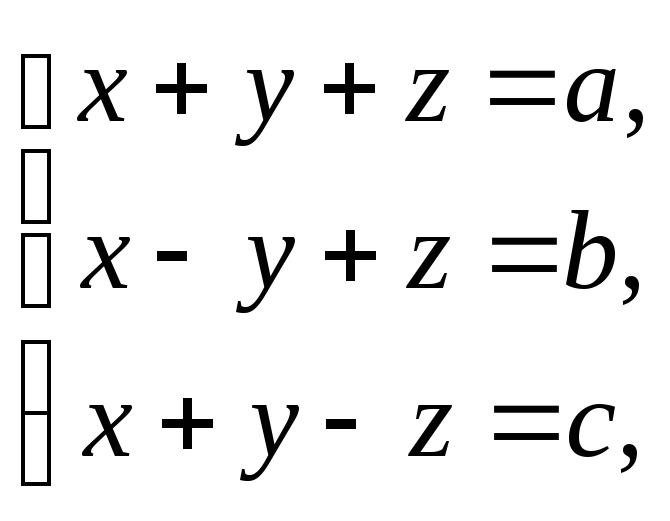 1243.
1243.
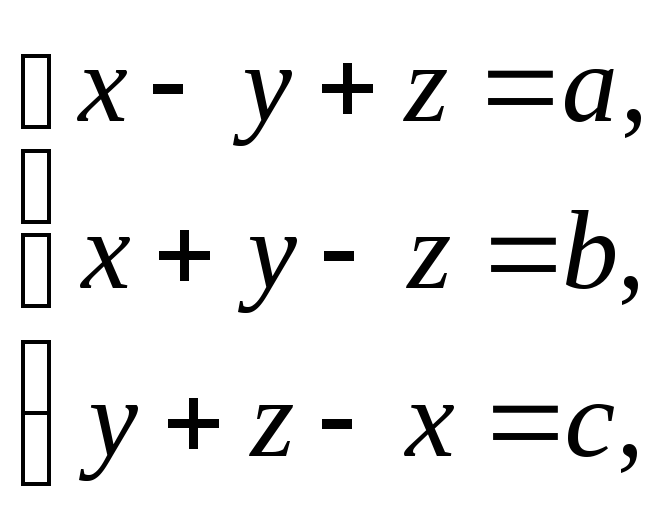 .
.
1244. Найти все решения системы
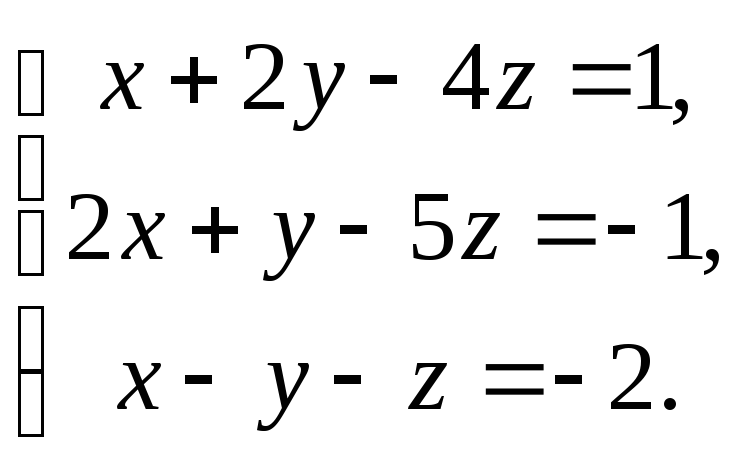
1245. Найти все решения системы
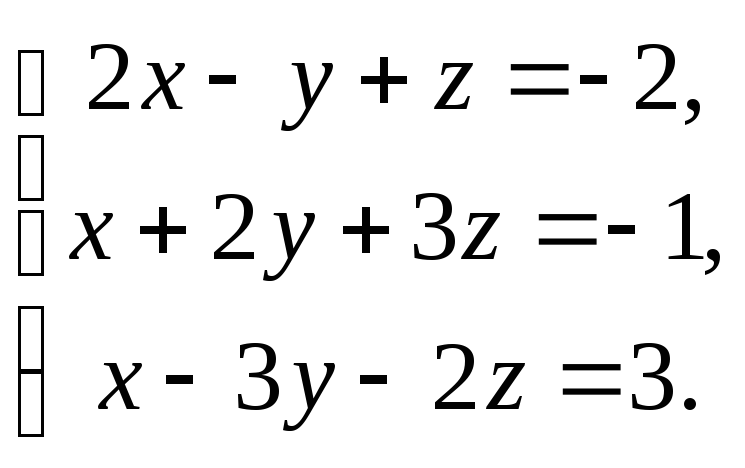
1246. Найти все решения системы
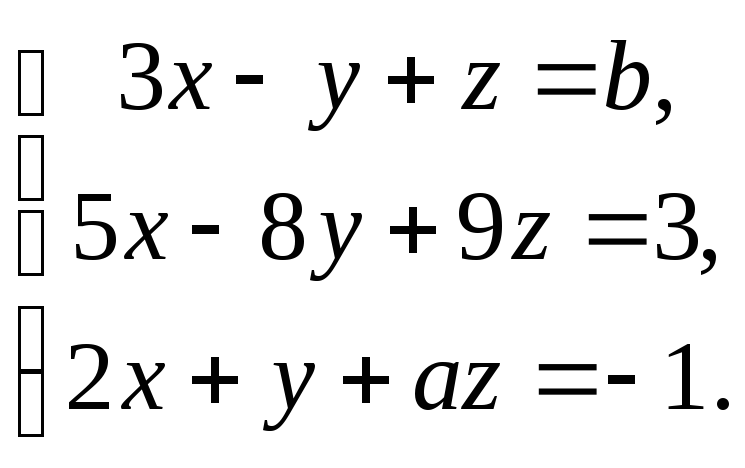
1247. Определить, при каких значениях а и b система уравнений
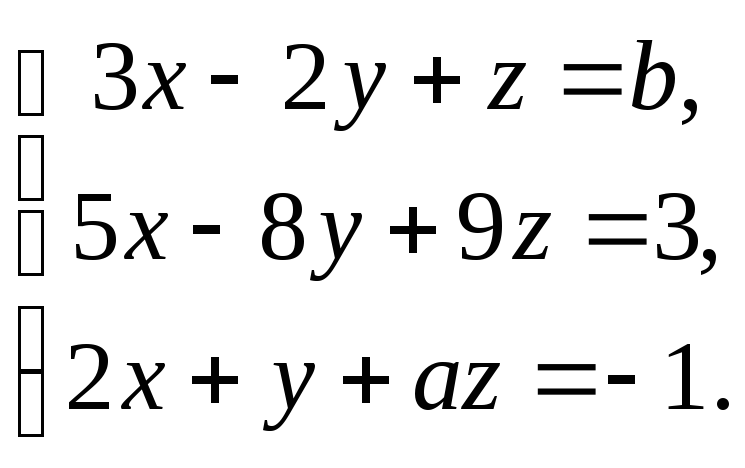
1) имеет единственное решение; 2) не имеет решений; 3) имеет бесконечно много решений.
1248. Доказать, что если система
уравнений
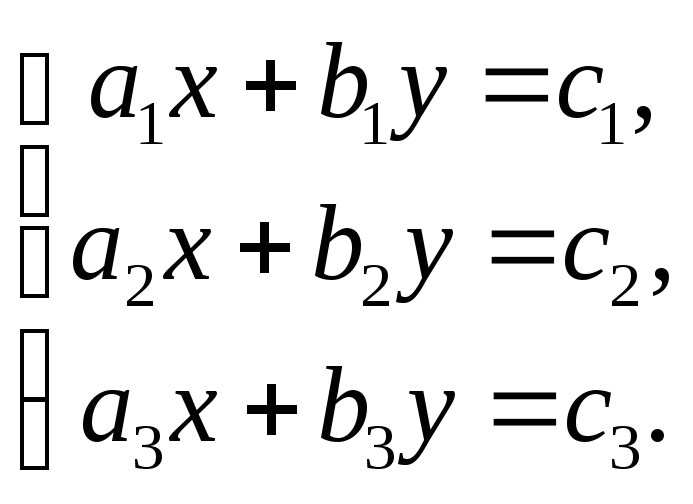
совместна, то
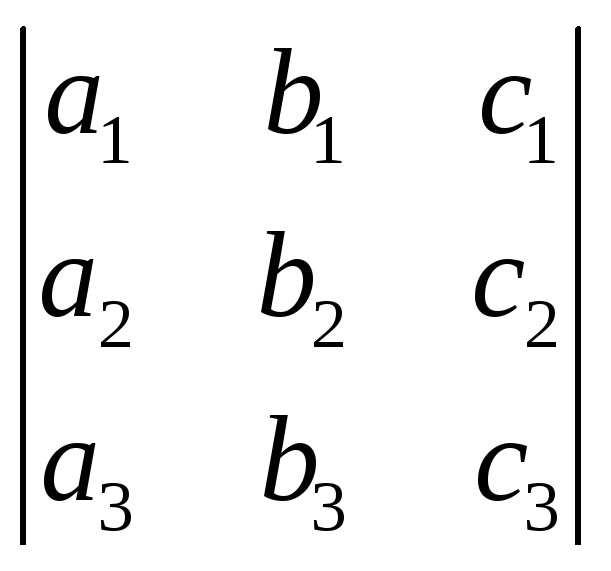 =
0
=
0
1249. Найти
все решения
системы
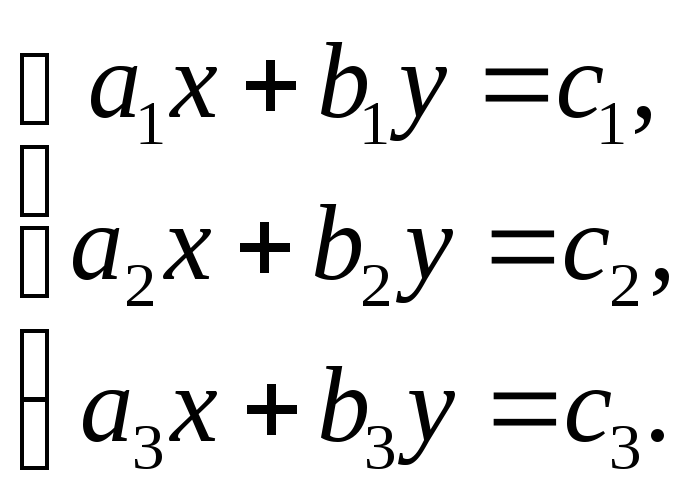
1250. Найти все решения системы
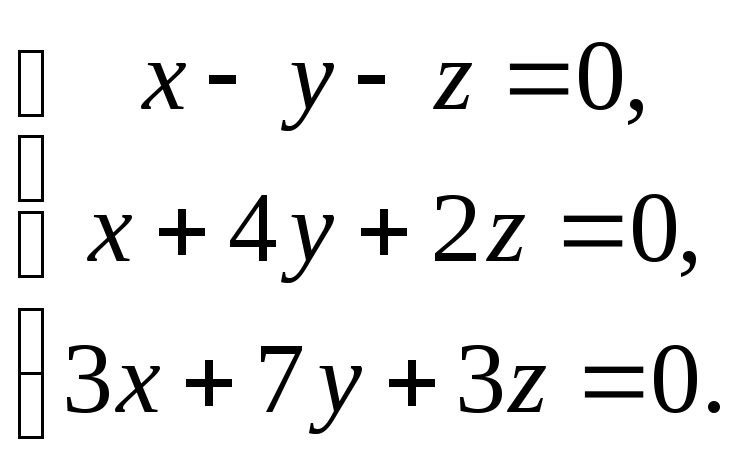
1251. Определить, при каком значении а система однородных уравнений
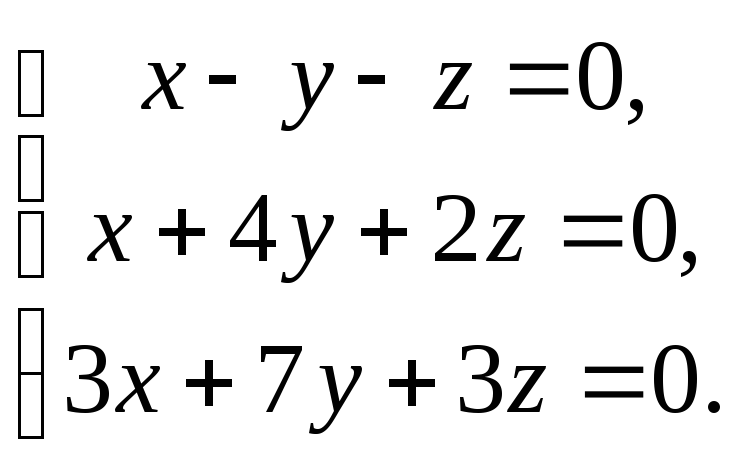
имеет ненулевое решение.