Файл: Метод РИПСА в задаче выбора решений (1. Системы поддержки принятия решений).pdf

В начале восьмидесятых годов в исследованиях по искусственному интеллекту сформировалось самостоятельное направление, получившее название "экспертные системы" (ЭС). Цель исследований по ЭС состоит в разработке программ, которые при решении задач, трудных для человека, получают результаты, не уступающие по качеству и эффективности решениям, получаемым квалифицированным экспертом.

По мнению ведущих специалистов, в недалекой перспективе ЭС будут играть ведущую роль во всех фазах проектирования, разработки, производства, распределения, продажи, поддержки и оказания услуг, а технология ЭС, получившая коммерческое распространение, обеспечит революционный прорыв в интеграции приложений из готовых интеллектуально взаимодействующих модулей.

Уже сейчас технология экспертных систем используется для решения различных типов задач (предсказание, диагностика, планирование, конструирование, контроль, отладка, инструктаж, управление) в самых разнообразных проблемных областях, таких, как финансы, нефтяная и газовая промышленность, энергетика, транспорт, фармацевтическое производство, космос, металлургия, горное дело, химия, образование, целлюлозно-бумажная промышленность, телекоммуникации и связь и др.

ЭС предназначены для решения так называемых неформализованных задач. Неформализованные задачи обычно обладают следующими особенностями:

ошибочностью, неоднозначностью, неполнотой и противоречивостью исходных данных и знаний о проблемной области и решаемой задаче.
большой размерностью пространства решения, т.е. перебор при поиске решения весьма велик.
динамически изменяющимися данными и знаниями.

Экспертные системы и системы искусственного интеллекта отличаются от систем обработки данных тем, что в них в основном используются символьный (а не числовой) способ представления, символьный вывод и эвристический поиск решения (а не исполнение известного алгоритма).

Таким образом, мы видим, что мнения экспертов, которые превращаются в экспертной системе в знания, могут не совпадать и даже противоречить друг другу. Поэтому необходимо использовать специальные методы, которые могут достаточно надежно сопоставить различные элементы знания (альтернативы) в условиях, когда они оцениваются по разному. Если эти оценки можно принять в качестве некоторых критериев оптимальности, для решения указанной задачи можно привлечь такие методы, как MAUT (многокритериальная теория полезности), AHP(метод аналитической иерархии), ELECTRE(исключение и выбор, отражающие реальность), голосования (метод Борда и система де Кондорсе).

Поэтому избранная тема «Метод РИПСА в задаче выбора решений» является актуальной и подлежит рассмотрению в курсовой работе.

Целью курсовой работы является подробное изучение метода РИПСА и его применение на практике.

Для достижения поставленной цели необходимо решить следующие задачи исследования:

изучить системы поддержки принятия решений;
рассмотреть применение методов РИПСА на практике.

Предметом исследования является метод РИПСА.

Объектом — задача выбора решений.

Теоретической основой являются учебники и учебные пособия таких авторов, как Самков А. В., Азгальдов Г. Г., Саати Т. Л., Михалев А. И.

1. Системы поддержки принятия решений

1.1. Методы, основанные на количественном выражении предпочтений ЛПР на множестве критериев

Метод приращений

ЛПР выражает свои предпочтения на множестве критериев, как правило, с помощью задания системы весовых коэффициентов. Данные методы можно условно разделить на две группы:

1) простые методы объединения характеристик;

2) методы объединения, основанные на порогах чувствительности.

Одним из основных методов 1-й группы является простой метод приращений.

Входные данные – множество вариантов решения. Каждый из этих вариантов предварительно оценивают. Оценка производится по нескольким заданным критериям. При каждой оценке (по каждому критерию) вариант получает свой порядковый номер. Затем каждый вариант будет поставлен на какое-либо место. Это место определяется оценкой порядковых номеров критериев. Затем строится квадратная матрица. B=||bir|| порядка N. Значение bir показывает, сколько раз i-й вариант xi оценен как r-й по порядку.

Если заданы весовые коэффициенты, то bir – это сумма весов тех критериев, по которым вариант оценен по порядку, т.е. элементы матрицы можно интерпретировать как меру приращения r-го порядка i-му варианту.

Составляется матрица Y=||yir||, состоящая только из нулей и единиц. Изначально она вся нулевая. yir = 1, если варианту xi приписан r-й порядок. Для нахождения решения решается задача целочисленного линейного программирования:

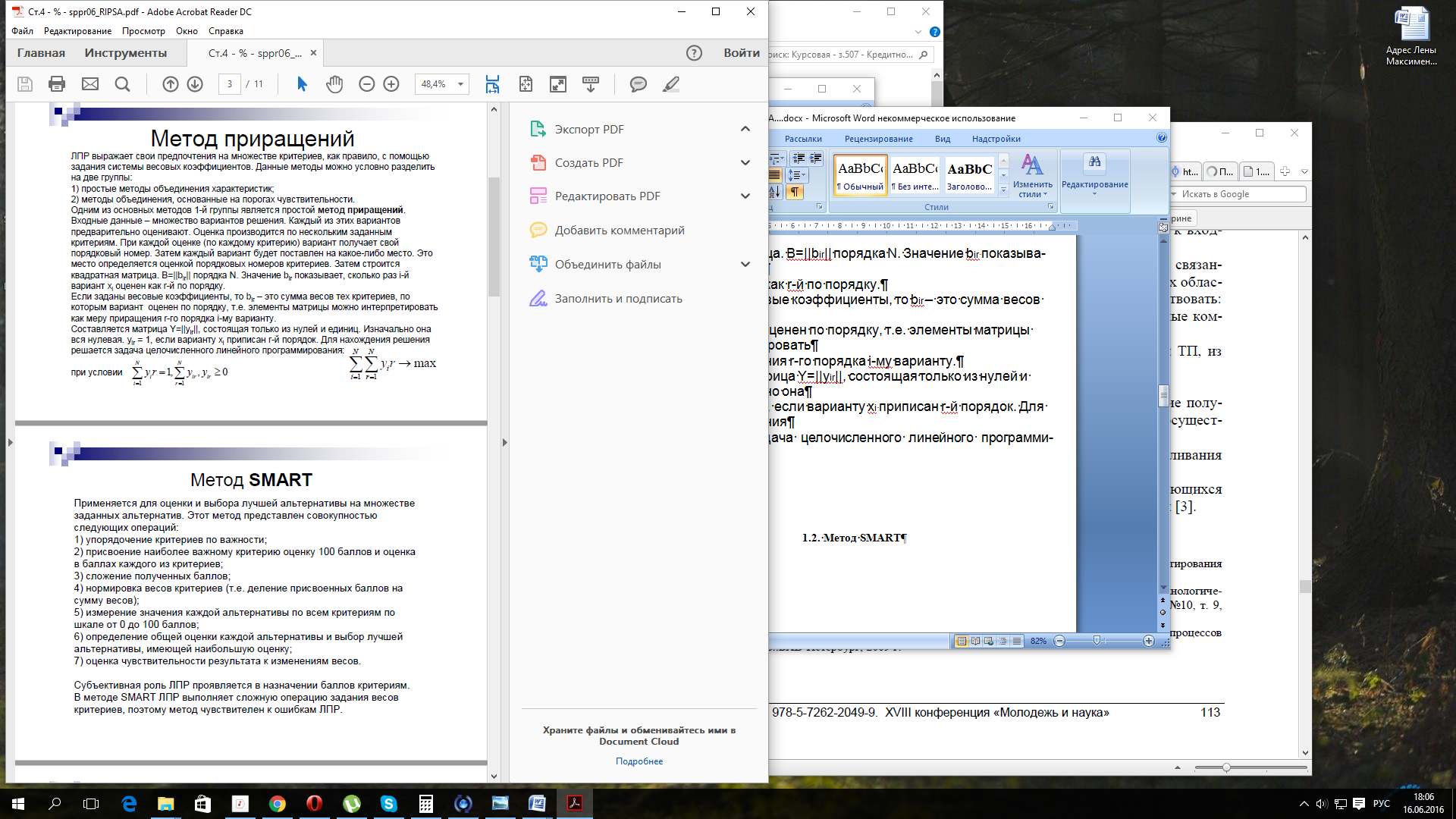(1.1)

при условии

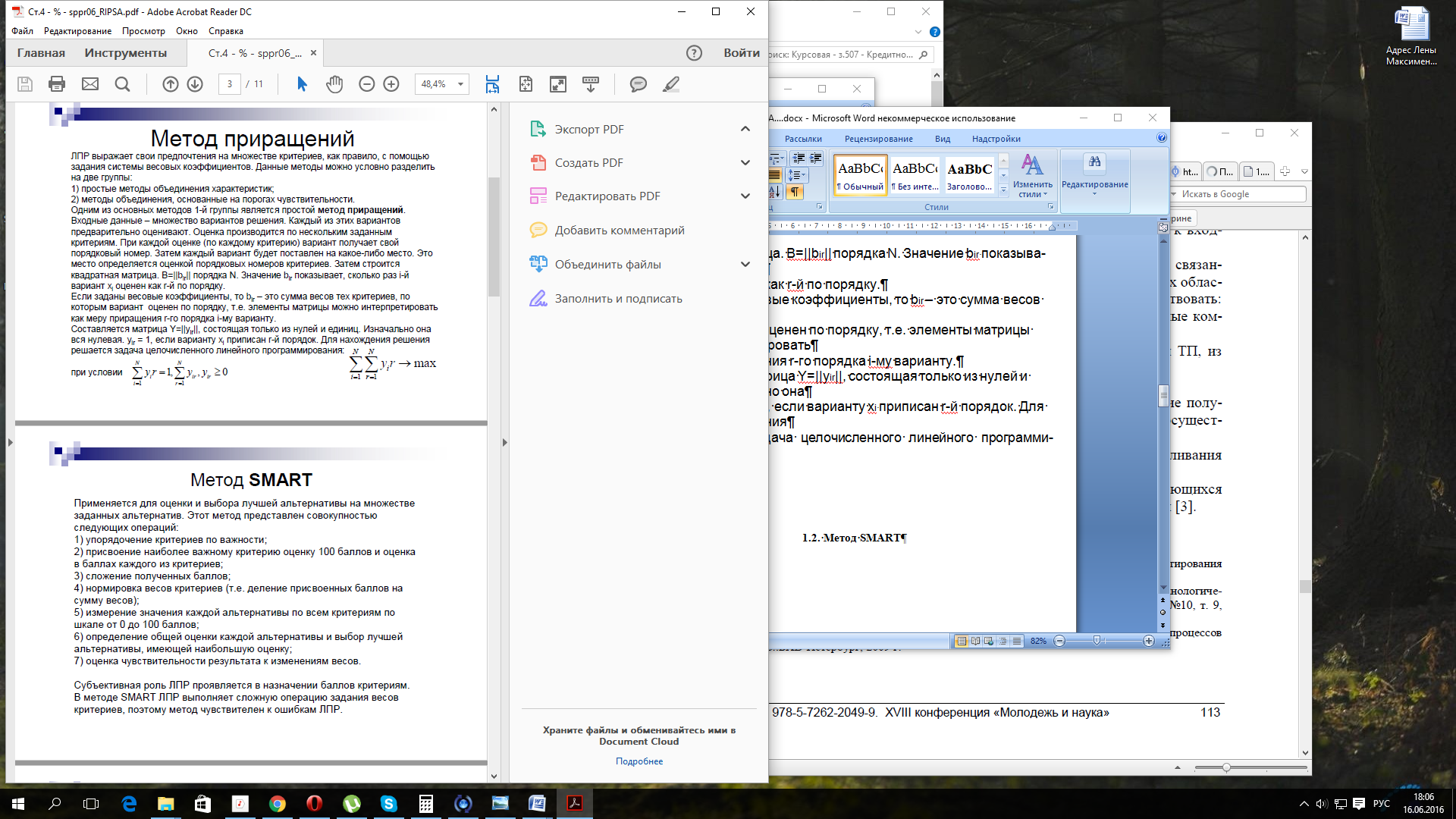(1.2)

1.2. Метод SMART

Применяется для оценки и выбора лучшей альтернативы на множестве заданных альтернатив. Этот метод представлен совокупностью следующих операций:

1) упорядочение критериев по важности;

2) присвоение наиболее важному критерию оценку 100 баллов и оценка в баллах каждого из критериев;

3) сложение полученных баллов;

4) нормировка весов критериев (т.е. деление присвоенных баллов на сумму весов);

5) измерение значения каждой альтернативы по всем критериям по шкале от 0 до 100 баллов;

6) определение общей оценки каждой альтернативы и выбор лучшей альтернативы, имеющей наибольшую оценку;

7) оценка чувствительности результата к изменениям весов.

Субъективная роль ЛПР проявляется в назначении баллов критериям.

В методе SMART ЛПР выполняет сложную операцию задания весов критериев, поэтому метод чувствителен к ошибкам ЛПР.

1.3. Методы объединения, основанные на порогах чувствительности: методы класса РИПСА

Основу этих методов составляют методы класса ЭЛЕКТРА (ЭЛЕКТРА 1, ЭЛЕКТРА 2, ЭЛЕКТРА 3), которые были разработана коллективом французских ученых, возглавляемым профессором Б. Руа. Эти методы относятся к классу методов Разработки Индексов Попарного Сравнения Альтернатив (РИПСА).

В подходе РИПСА принято различать 2 этапа:

1) этап разработки, на котором строятся один или несколько индексов попарного сравнения альтернатив;

2) этап исследования, на котором построенные индексы используются для ранжирования (или классификации) заданного множества альтернатив.

ЭЛЕКТРА 1 позволяет из множества вариантов исключить неэффективные варианты. В основе данного метода лежит попарное сравнение отдельных вариантов.

ЭЛЕКТРА 2 служит для упорядочения индифферентных классов вариантов.

ЭЛЕКТРА 3 отличается от метода ЭЛЕКТРА 2 способом задания порогов чувствительности.

1.3.1. Метод ЭЛЕКТРА 1

Входными данными для метода является множество решений. Метод отсекает все неэффективные варианты. На множестве вариантов Х производится попарное их сравнение, в результате которого строятся индексы согласия и несогласия.

Каждому из N критериев ставится в соответствие целое число w, характеризующее важность критерия (фактически, вес критерия). Это число можно получить как количество голосов жюри, поданных за этот критерий.

Выдвигается гипотеза о превосходстве альтернативы Ai над альтернативой Aj. Множество I, состоящее из N критериев, разбивается на 3 подмножества:

I+ – подмножество критериев, по которым Ai предпочтительнее Aj.

I- – подмножество критериев, по которым Aj предпочтительнее Ai.

I= – подмножество критериев, по которым Ai равноценна Aj.

Далее формируется индекс согласия с гипотезой о превосходстве Ai над Aj:

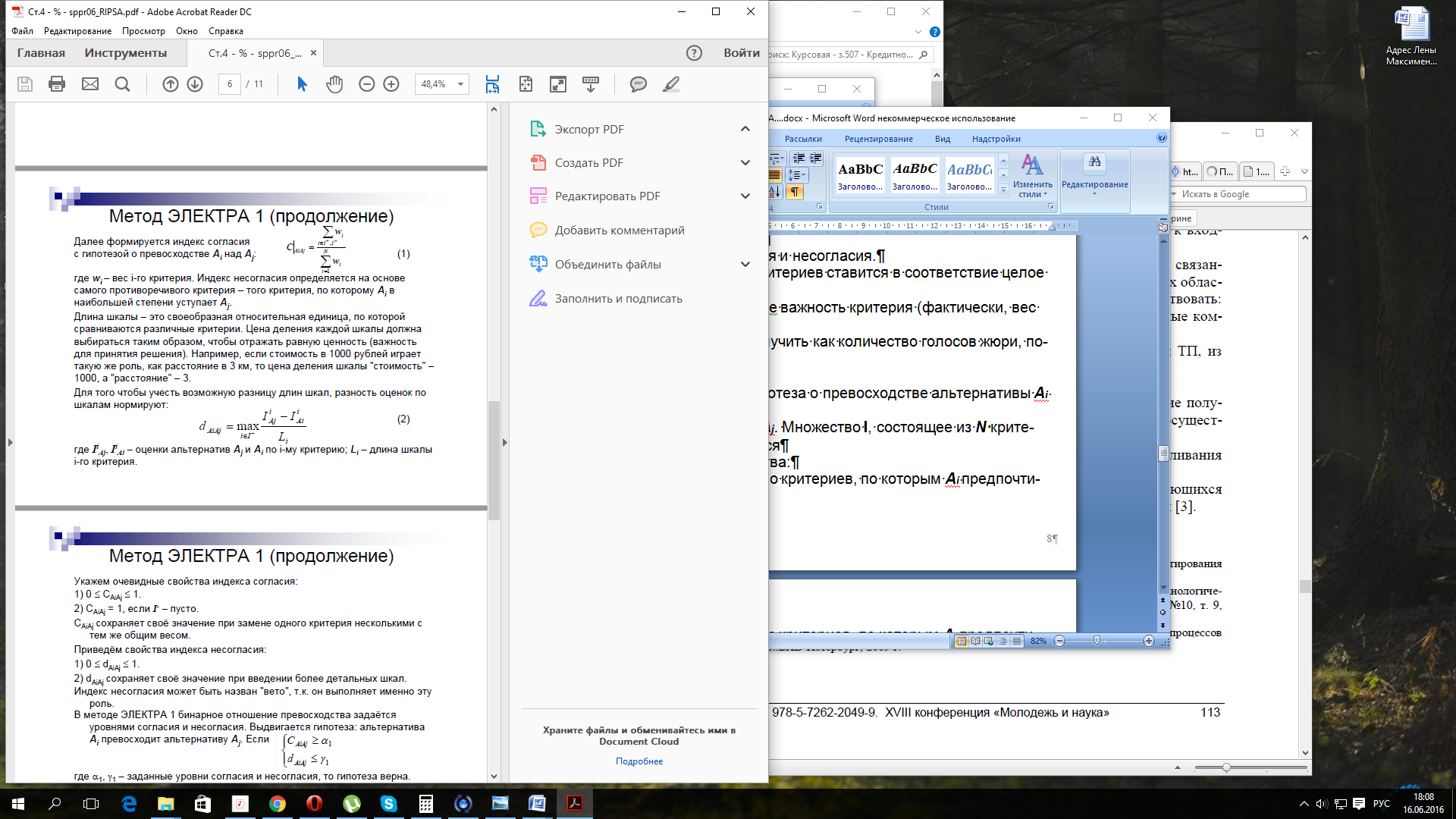(1.3)

где wi – вес i-го критерия. Индекс несогласия определяется на основе самого противоречивого критерия – того критерия, по которому Ai в наибольшей степени уступает Aj.

Длина шкалы – это своеобразная относительная единица, по которой сравниваются различные критерии. Цена деления каждой шкалы должна выбираться таким образом, чтобы отражать равную ценность (важность для принятия решения). Например, если стоимость в 1000 рублей играет такую же роль, как расстояние в 3 км, то цена деления шкалы "стоимость" – 1000, а "расстояние" – 3.

Для того чтобы учесть возможную разницу длин шкал, разность оценок по шкалам нормируют:

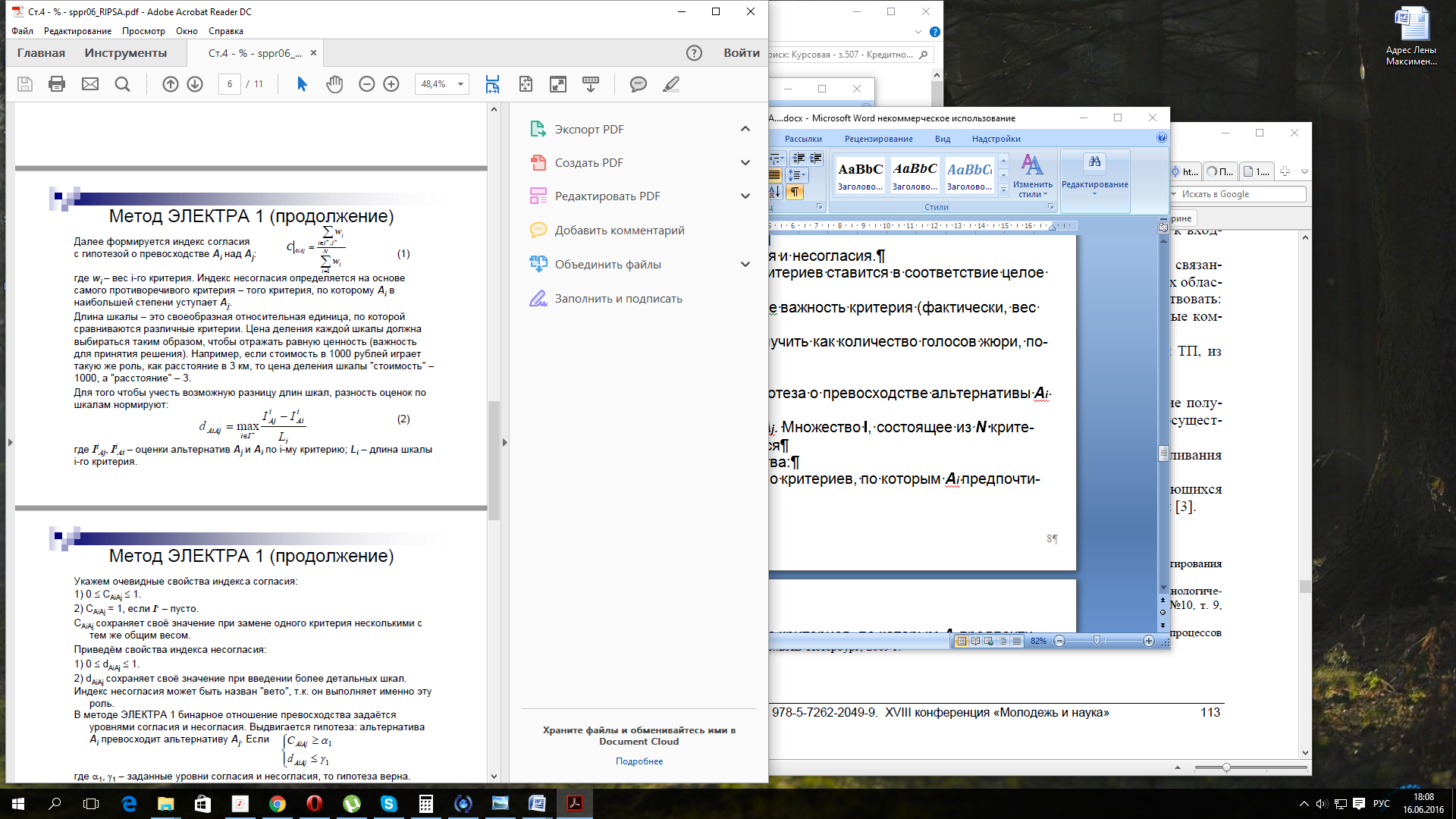(1.4)

где Ii Aj, Ii Ai – оценки альтернатив Aj и Ai по i-му критерию; Li – длина шкалы i-го критерия.

Укажем очевидные свойства индекса согласия:

1) 0 ≤ СAiAj ≤ 1.

2) СAiAj = 1, если I- – пусто.

СAiAj сохраняет своё значение при замене одного критерия несколькими с тем же общим весом.

Приведём свойства индекса несогласия:

1) 0 ≤ dAiAj ≤ 1.

2) dAiAj сохраняет своё значение при введении более детальных шкал.

Индекс несогласия может быть назван "вето", т.к. он выполняет именно эту роль.

В методе ЭЛЕКТРА 1 бинарное отношение превосходства задаётся уровнями согласия и несогласия. Выдвигается гипотеза: альтернатива Ai превосходит альтернативу Aj. Если

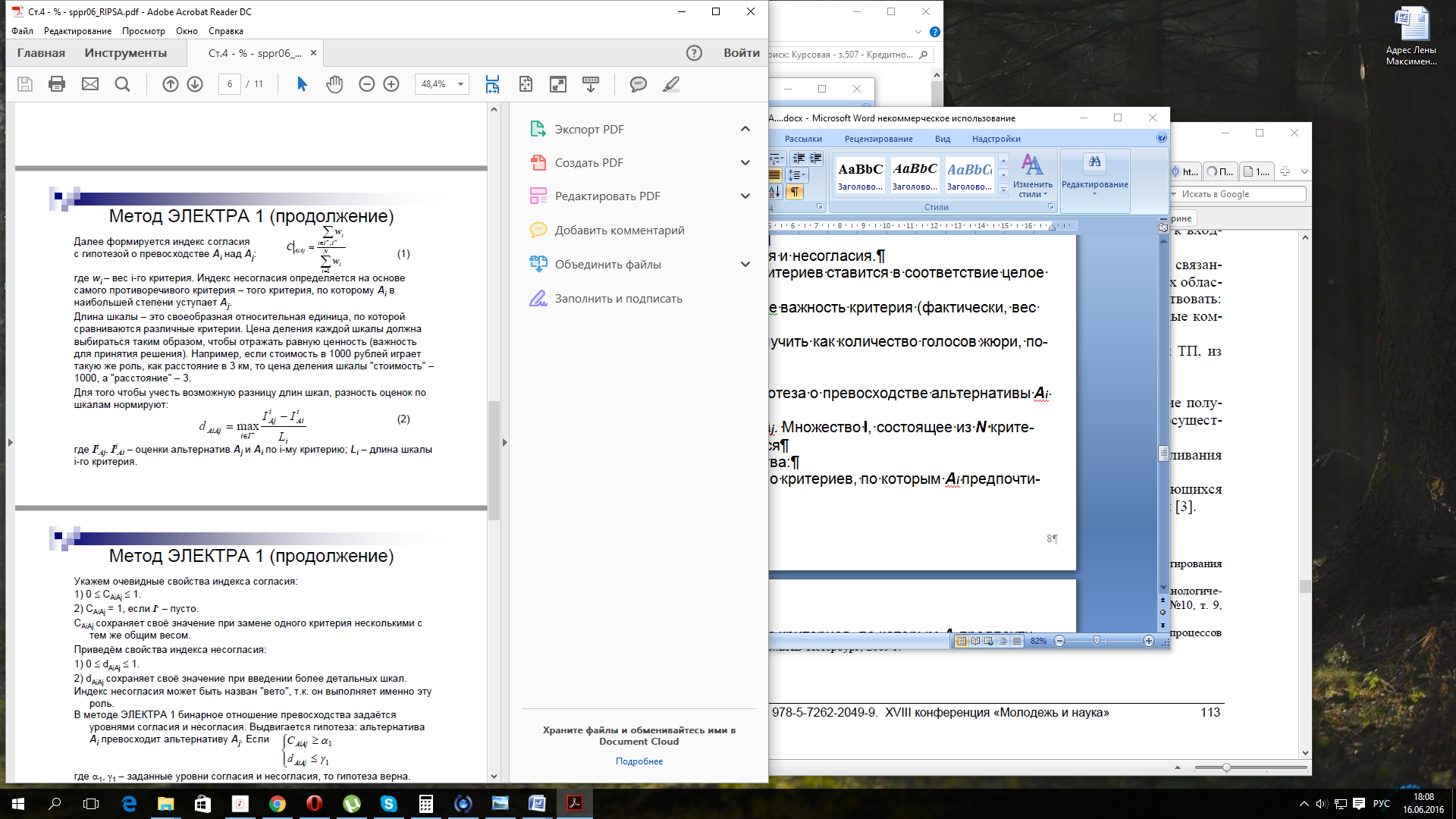(1.5)

где α1, γ1– заданные уровни согласия и несогласия, то гипотеза верна.

Если же при этих уровнях альтернативы не удаётся сравнить, то они объявляются несравнимыми.

При заданных условиях выделяется ядро недоминируемых альтернатив.

При изменении уровней α и γ выделяется меньшее ядро и т.д., пока не будет исчерпан весь список альтернатив. В последнее ядро входят лучшие альтернативы. В конечном итоге получается групповая ранжировка альтернатив по качеству.

Для каждой пары вариантов xi и xj определяются еще два множества:

множество согласований Gij и множество рассогласований Dij.

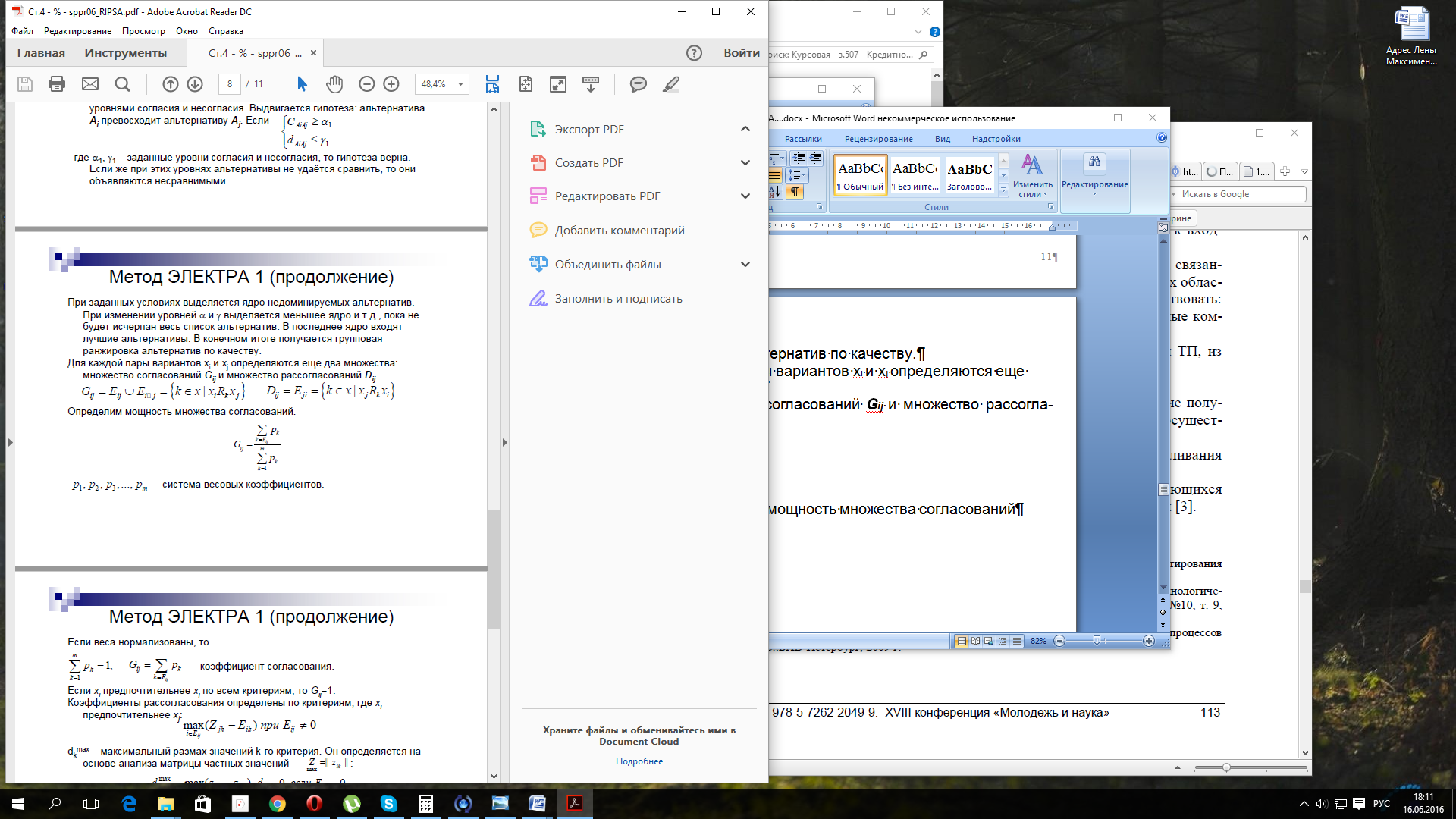(1.6)

Определим мощность множества согласований

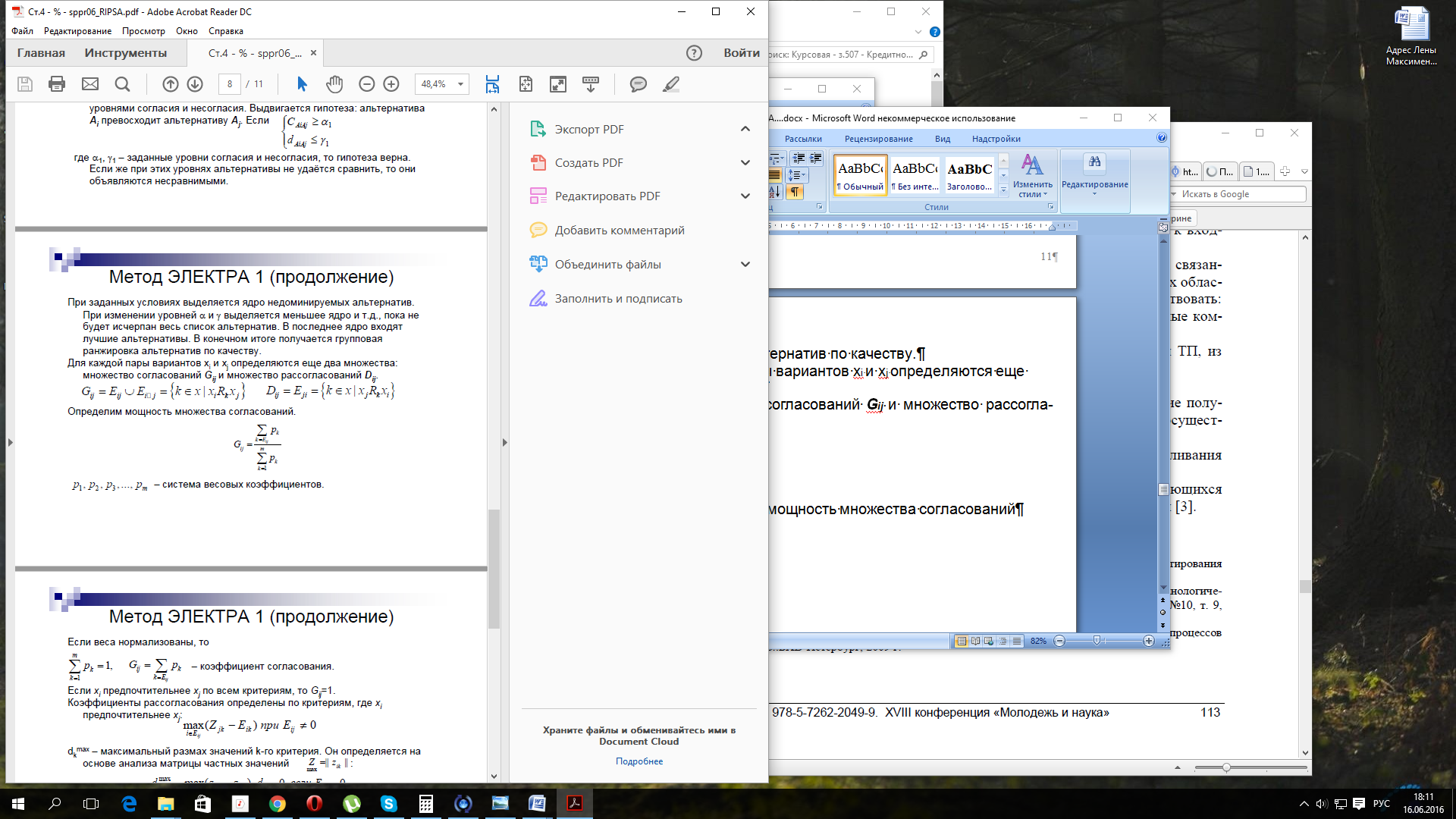(1.7)

р1, р2, р3, ... рm — система весовых коэффициентов.

Если веса нормализованы, то

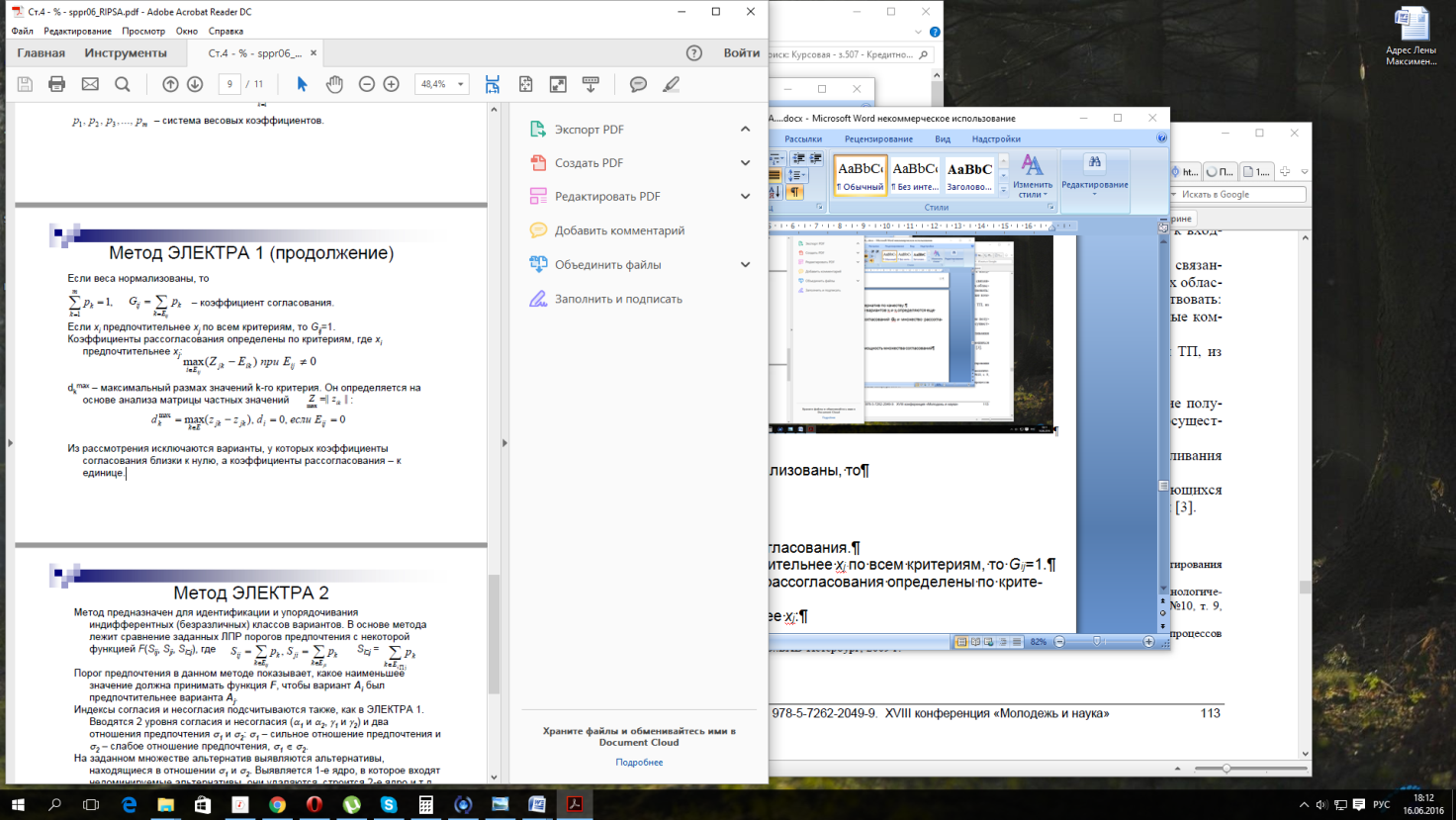— коэффициент согласования. (1.8)

Если xi предпочтительнее xj по всем критериям, то Gij=1.

Коэффициенты рассогласования определены по критериям, где xi предпочтительнее xj:

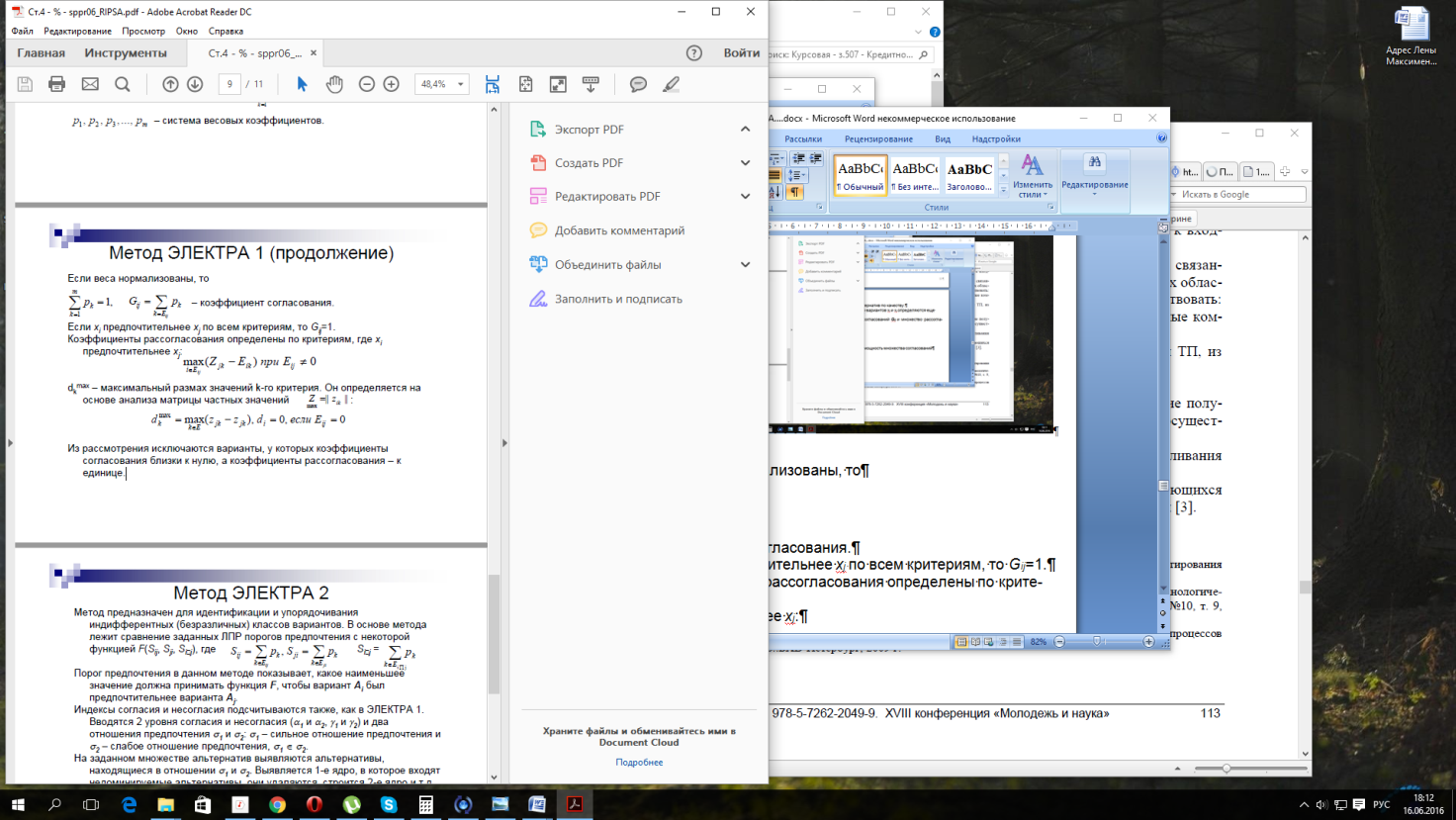(1.9)

dk max – максимальный размах значений k-го критерия. Он определяется на основе анализа матрицы частных значений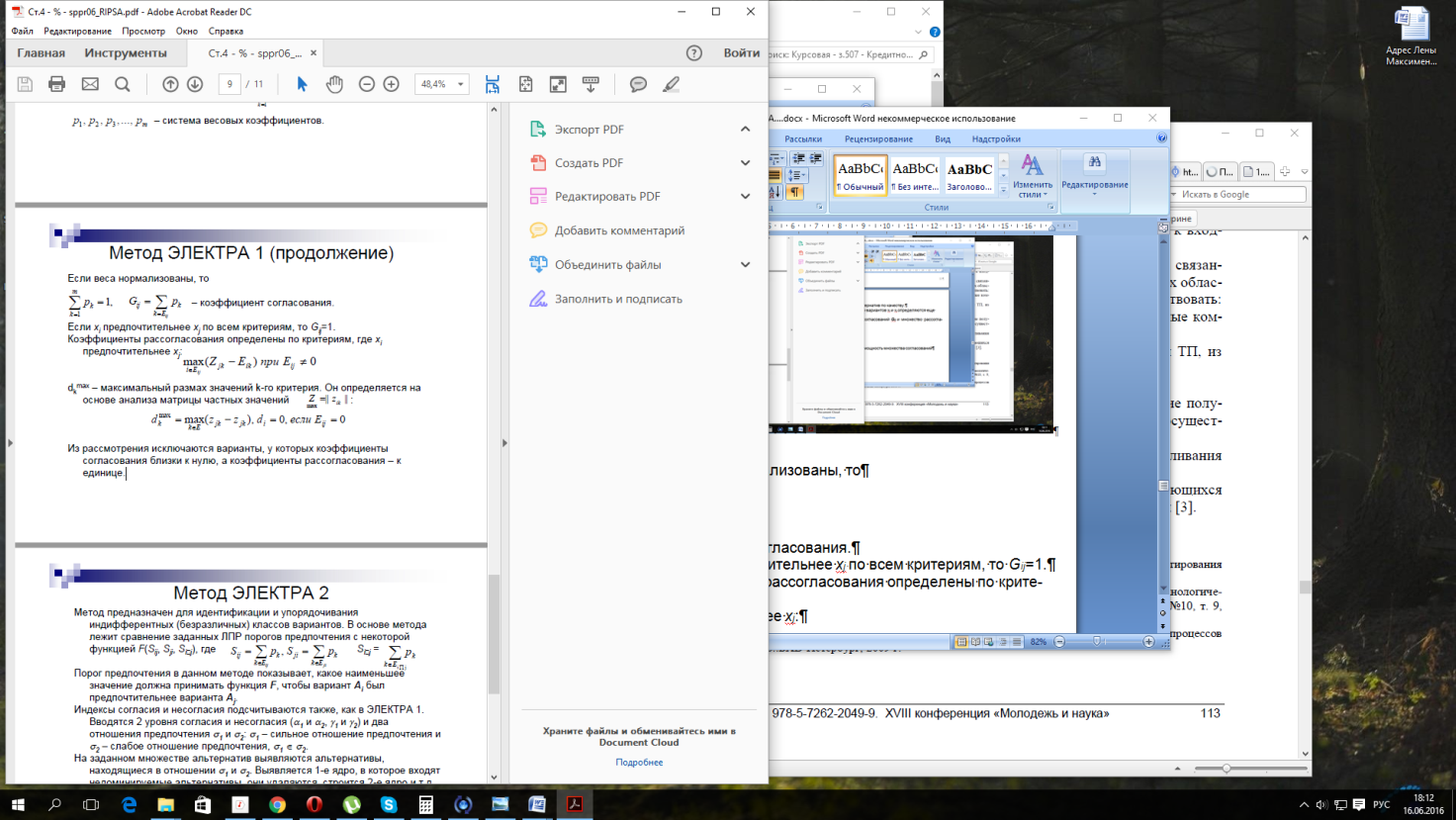

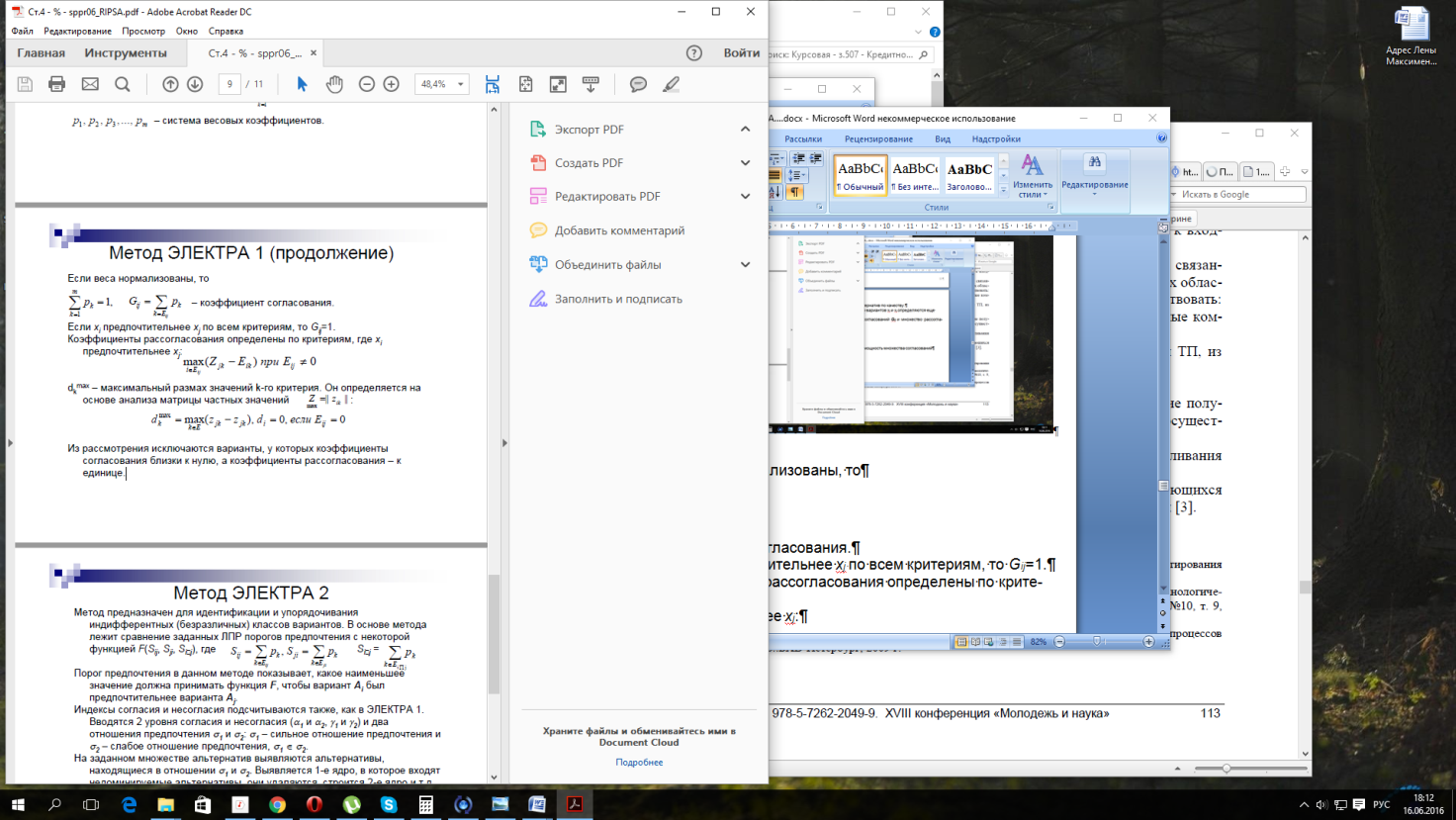(1.10)

Из рассмотрения исключаются варианты, у которых коэффициенты согласования близки к нулю, а коэффициенты рассогласования – к единице.

1.3.2. Метод ЭЛЕКТРА 2

Метод предназначен для идентификации и упорядочивания индифферентных (безразличных) классов вариантов. В основе метода лежит сравнение заданных ЛПР порогов предпочтения с некоторой функцией F(Sij, Sji, Si????j), где

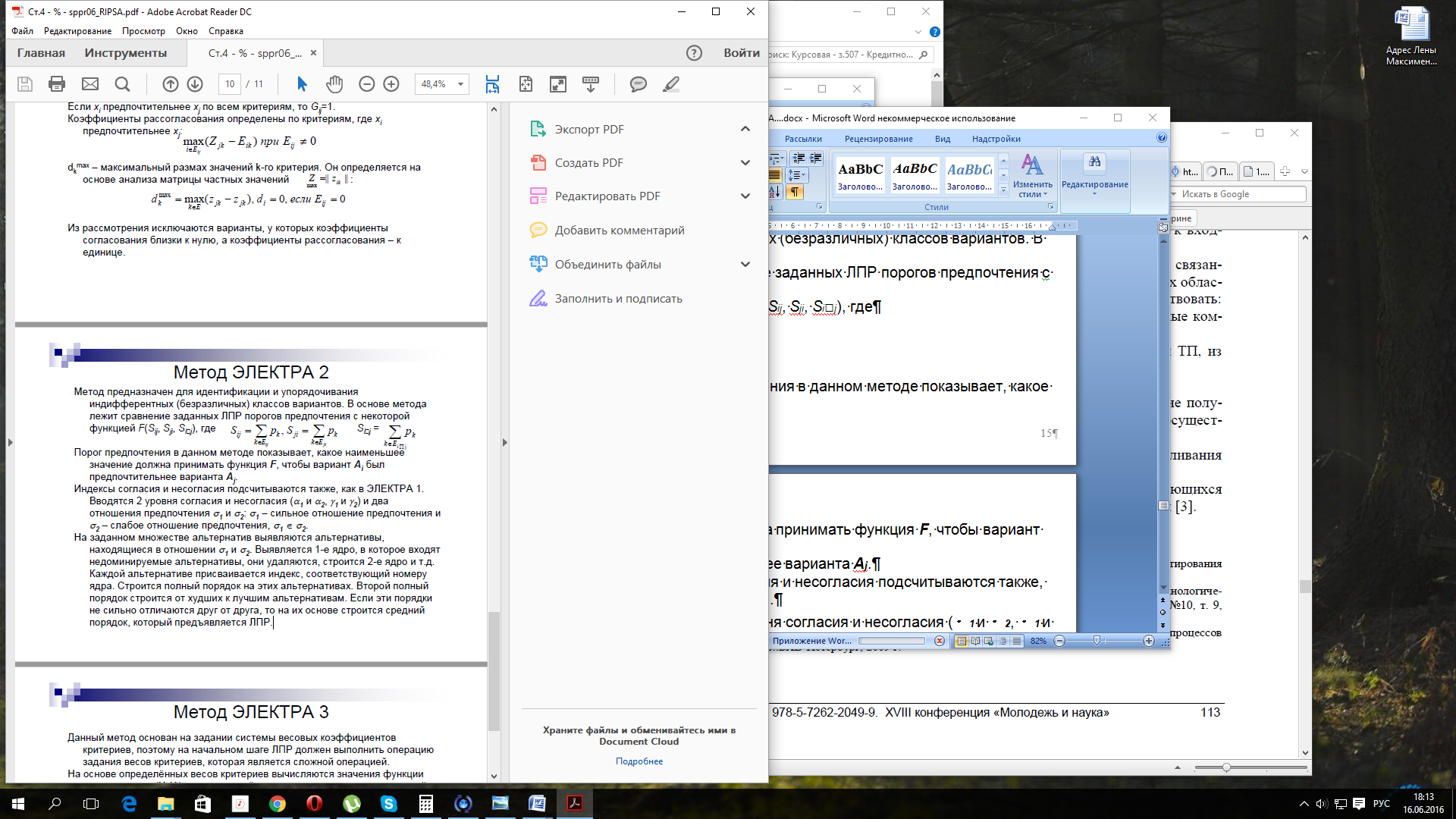(1.11)

Порог предпочтения в данном методе показывает, какое наименьшее значение должна принимать функция F, чтобы вариант Аi был предпочтительнее варианта Аj.

Индексы согласия и несогласия подсчитываются также, как в ЭЛЕКТРА 1.

Вводятся 2 уровня согласия и несогласия (α1 и α2, γ1 и γ2) и два отношения предпочтения σ1 и σ2: σ1 – сильное отношение предпочтения и σ2 – слабое отношение предпочтения, σ1 принадлежит σ2.