Файл: Кафедра атп курсовая работа по Теории автоматического управления на тему система автоматического регулирования старков С. Л гр. Атп324 Проверил Коуров Г. Н. Уфа2022 Содержание.docx

M_C






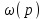
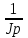
М(p)- M_C



U(p)

U(p)-E(p)




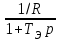
I(p)

C_MФ


M(p)








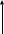
E(p)


C_eФ




Все характеристики двигателя рассчитаем следующим образом:

1/Rя=0.592 Тэ=Lя/Rя=0.03787

Сe=(Uн-Iян*Rя)/ωн Сm=J*ωн/Iя, где ωн=78.5 рад/с, Uн=220 В, J=0.23*3, Iян=Pн/(ή*Uя)=11.6

Се*Φ=5.35 См*Ф=0.208

Передаточное устройство является линейным звеном. Зная номинальные значения частоты вращения вала двигателя и подачи на зуб фрезерного станка, запишем передаточную функцию:



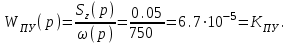
Процесс резания как объект управления с учетом возмущений опишем используя формулу (4). Но описанный процесс резания будет нелинейным звеном, а в данной части ТАУ мы изучаем линейные звенья. Поэтому нам придется лианеризовать это звено. Для этого построим график изменения погрешности обработки от подачи и проведем касательную в рабочей точке этой зависимости.

---

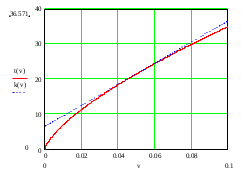S[мм/зуб]

Таким образом, процесс резания предстанет в следующем виде:


Δ

S_z(p)

K*S_z(p)

K








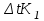
X₀


K₁





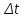
Где К – тангенс угла наклона касательной к графику в рабочей точке. К=300.7. X₀ – отклонение касательной от начала координат. X₀=6.5. 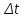- возмущение, действующее на систему. K₁ – коэффициент передачи системы при действии возмущения.

Датчик обратной связи, Wду(р)=Кду/(Тду*р+1), тогда Wду(р)=5 В/14.76=0.3388

Wду(р)=0.3388 В/мкм

Учитывая все сказанное выше составляется структурная схема.

---

Wпр(р)

Wпу(р)

Wдв(р)

Wпэ(р)

Wус(р)

Wку(р)
Uз ε Uку 10 В Uн w S Δ







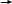
E

Wду(р)


Усилитель УС. Для обеспечения требуемых свойств САР его ткоэффициент принимаем Кус=999, т.к. Δз=Δр/(1+Крс), где Δз=0.001*Δр, тогда Крс= 999=Кус*Кпэ*Кд*Кпу*Кпр*Кду=1*Кус, откуда Кус=999.

4 Анализ устойчивости некорректированной САР

Для того, чтобы установить устойчива система или нет, воспользуемся логарифмическим критерием устойчивости. Для этого построим логарифмическую амплитудно-частотную характеристику и логарифмическую фазо-частотную характеристику разомкнутой системы. Передаточная функция разомкнутой системы будет выглядеть следующим образом:

W_РС(р)=W_ЗС(p)*W_ОС(p)=(0,187*22*0,000067*9,54*999*295*0,3388)/((1+0,17р)(1+0,107р)(0,03965р+1,05р+1))

Используя эту передаточную функцию строим ЛЧХ и ЛФХ:

L(дб)

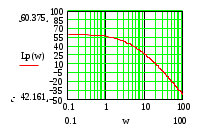lg(ω),ω(1/с)

φ(град)

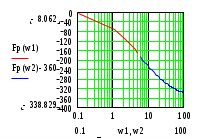lg(ω),ω(1/с)
По графику переходного процесса видим, что некорректированная САР является неустойчивой, т.к. ЛАХ пересекает ось абсцисс позже, чем кривая ЛФХ пересекает -180. Из графиков видно, что система не удовлетворяет предъявляемым требованиям. Необходимо применение корректирующего устройства.

5 Выбор корректирующего устройства

---

Из графиков ЛФХ и ЛЧХ, представленных в предыдущем пункте видно, что кривые необходимо «приподнять». Значит нам необходимо корректирующее устройство с запаздыванием по фазе. Нам подходит последовательно введенное корректирующее устройство, передаточная функция которого:

.

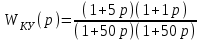Примером интегродифференцирующего контура может служить схема














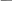
Коэффициенты подобраны таким образом, чтобы система имела максимальное быстродействие и не была колебательной. ЛФХ и ЛЧХ будут выглядеть следующим образом:

L(дб)

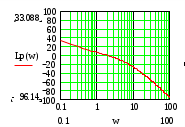lg(ω), ω(1/c)

φ(град)

---

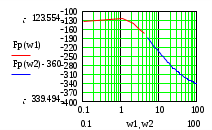lg(ω), ω(1/c)
Из графиков видно, что система имеет хорошие запасы устойчивости по модулю порядка 12 дб, по фазе порядка 60°. Быстродействие позволит системе быстро реагировать на возмущения, а параметры устойчивости не позволят вывести САР из равновесия.

6 Анализ качества САР

Для того, чтобы проанализировать качество проектируемой САР построим переходные процессы.

Переходной процесс выходной координаты при изменении управляющего воздействия для разомкнутой САР:

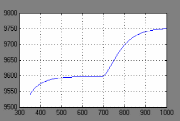t,с
Переходной процесс выходной координаты при изменении возмущения для разомкнутой САР:

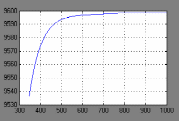
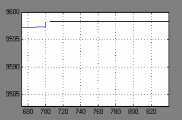t,с
Переходной процесс выходной координаты при изменении управляющего воздействия для замкнутой разработанной САР(на 15 секунде):
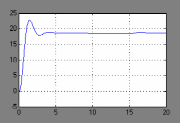
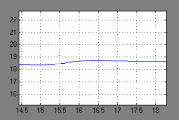t,с

Переходной процесс выходной координаты при изменении возмущения для замкнутой разработанной САР(на 15 секунде):

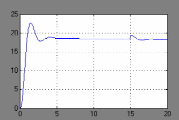
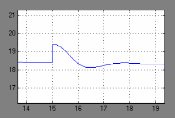t, с
Из графика переходного процесса видно, что система устойчива.

При изменении t_п от t_{п ном} = 0.7 мм до t_{п max} = 1,0мм (на 60 секунде) погрешность обработки изменяется от 18,49 до 18,48 мкм, что и необходимо было получить.

По построенным переходным процессам мы можем судить о качестве разработанной САР. Разработанная САР удовлетворяет заданным показателям качества. Система имеет хорошее быстродействие (время переходного процесса 5 секунд), что позволяет ей быстро реагировать на действие возмущений, величина перерегулирования 25%.

Заключение

В настоящее время в промышленности и сельском хозяйстве применяют десятки тысяч различных типов систем автоматического регулирования (САР), которые обеспечивают высокую эффективность производственных процессов.

Была спроектирована система автоматического регулирования погрешности обработки при фрезеровании. Система удовлетворяет всем требуемым параметрам. Выбранный и использованный в проектировании метод с использованием ЛЧХ очень удобен благодаря своей простоте

---