Файл: Отчет по лабораторным работам по дисциплине Основы Передачи Данных.docx
Добавлен: 08.11.2023
Просмотров: 13
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
ИНИСТЕРСТВО НАУКИ И ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)»
| Институт №3 | Кафедра №301 |
Отчет по лабораторным работам
по дисциплине
«Основы Передачи Данных»
Выполнили: студенты гр.М30-302Бки-20
Кхайрил Мирза Шах Бин Базерин
Нур Вахида Бинти Камарудин
Ник Назмир Надим Бин Ник Азлан
Принял доцент кафедры 301 :
Коробков Кирилл Андреевич
Москва – 2023
СОДЕРЖАНИЕ
ЛАБОРАТОРНАЯ РАБОТА 2 3
ЛАБОРАТОРНАЯ РАБОТА 2
Исследование Полей Галуа и его арифметики
Для работы с информацией при кодировании и декодировании данных все арифметические операции выполняются в полях Галуа. Применяется так называемая полиномиальная арифметика или арифметика полей Галуа. Таким образом, результат любой операции также является элементом этого поля.
Конкретное поле Галуа состоит из фиксированного диапазона чисел. Характеристикой поля называется некоторое простое число p. Порядок поля, т.е. число его элементов, является некоторой естественной степенью характеристики pm, где m∈N. При m = 1 поле называется простым.
В случаях, когда m> 1, для формирования поля также требуется порождающий многочлен степени m; такое поле называется расширенным. GF (p ^ m) - это обозначение поля Галуа.
В этой работе мы создали модель в MATLAB для расчета по полю Галуа.
Мы использовали производящий многочлен -
.
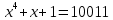
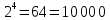
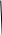
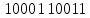
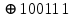
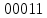=3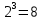 
Так, это поле состоит из чисел от 0 до 7.
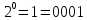
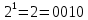
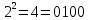
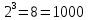
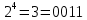
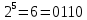
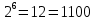
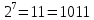
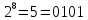
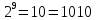
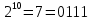
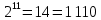
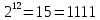
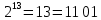
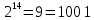
Затем мы построили модельную схему, способную преобразовывать и вычислять сложение и умножение чисел в поле Галуа.
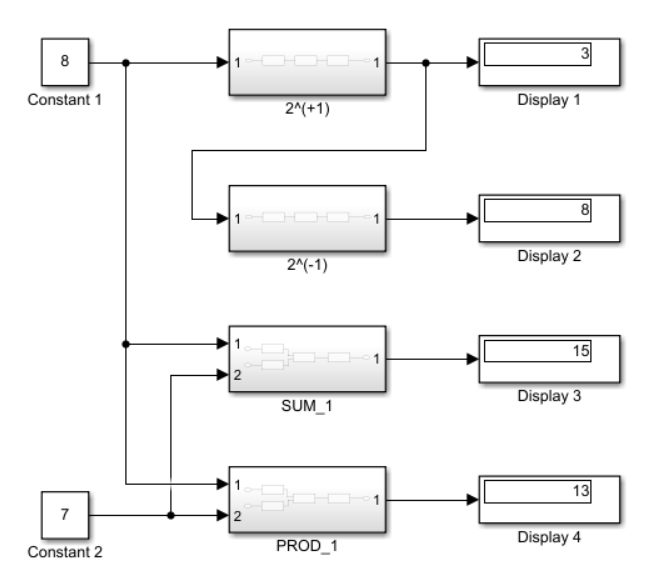
Рисунок 1. показана полная схема модели с 4 подсистемами:
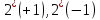, SUM_1, PROD_1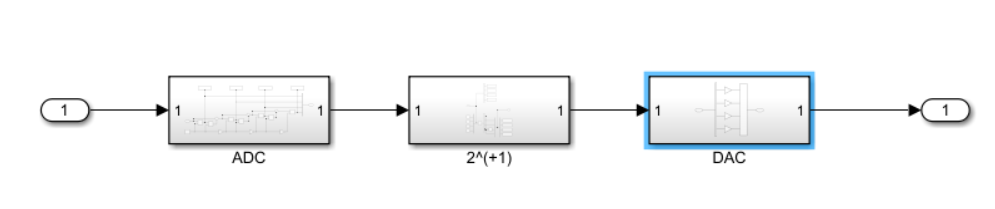
На рисунке 2. показана подсистема
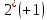
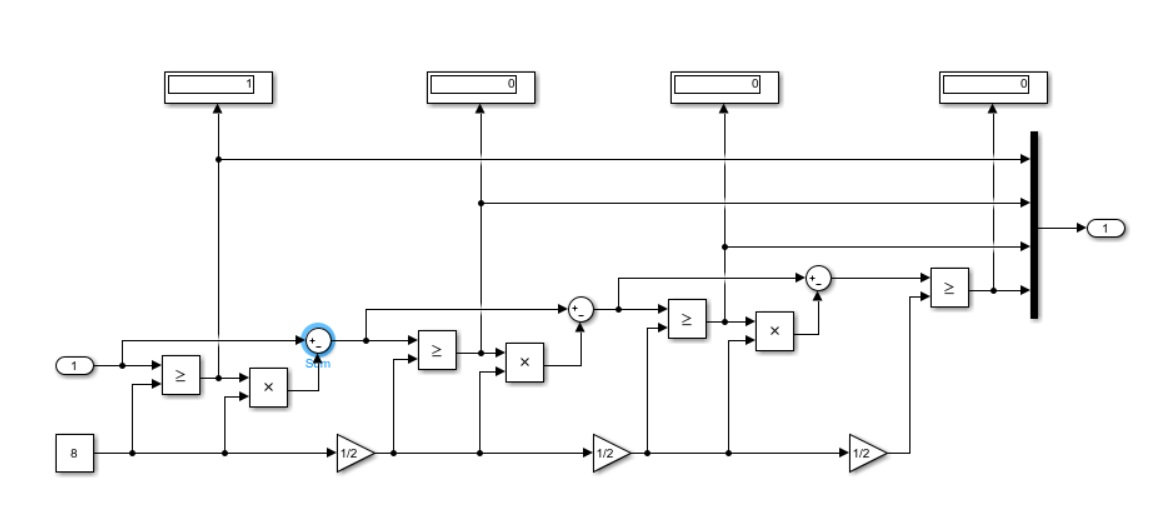
На рисунке 3. показана подсистема ADC.
В этой подсистеме мы преобразуем число из десятичного в двоичное.
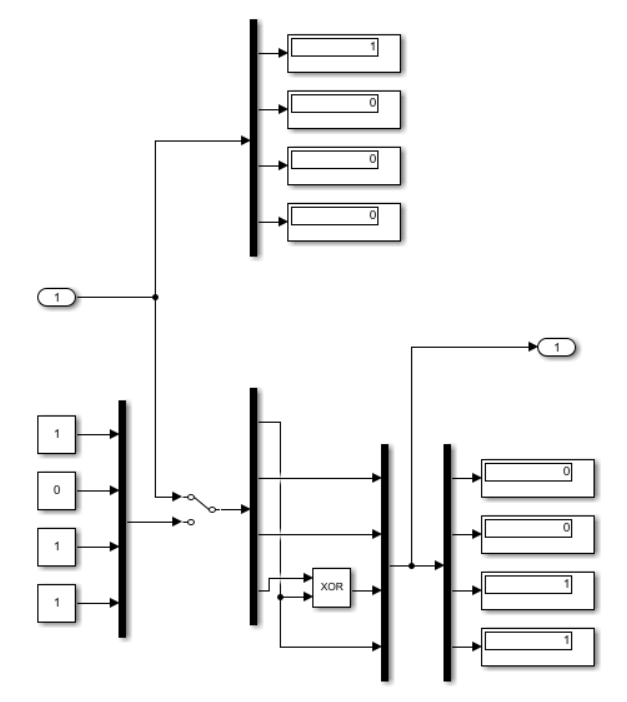
На рисунке 4. показана подсистема
.В этой подсистеме двоичный код переворачивается, а затем последняя и первая цифры суммируются по модулю 2. Результат будет использован в качестве 2-й последней цифры. затем окончательный номер передается в подсистему DAC.
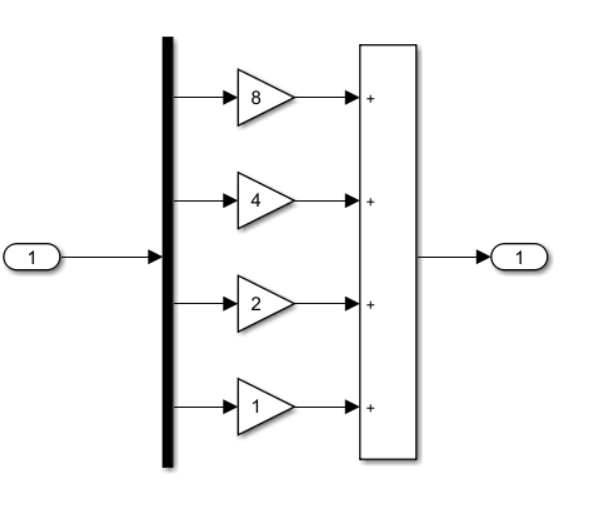
На рисунке 5. показана подсистема DAC.
В этой подсистеме мы преобразуем число из двоичного в десятичное.
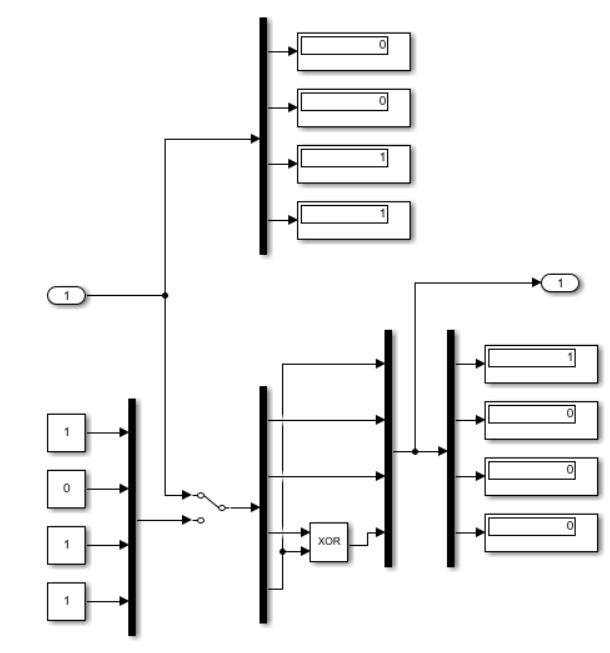
На рисунке 4. показана подсистема
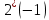.Эта подсистема аналогична подсистеме
и преобразует обратно число в исходные входные данные.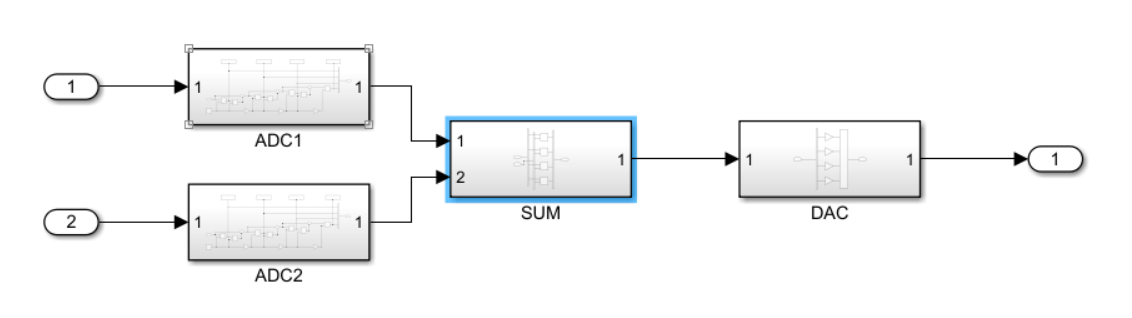
На рисунке5. Указана система SUM_1, состоящая из 2 подсистем ADC, 1 подсистемы SUM и 1 подсистемы DAC.
В этой подсистеме мы используем подсистему АЦП для преобразования числа в двоичный код и подсистему SUM для вычисления сложения двух чисел. И, наконец, подсистема DAC для преобразования обратно в десятичный формат.
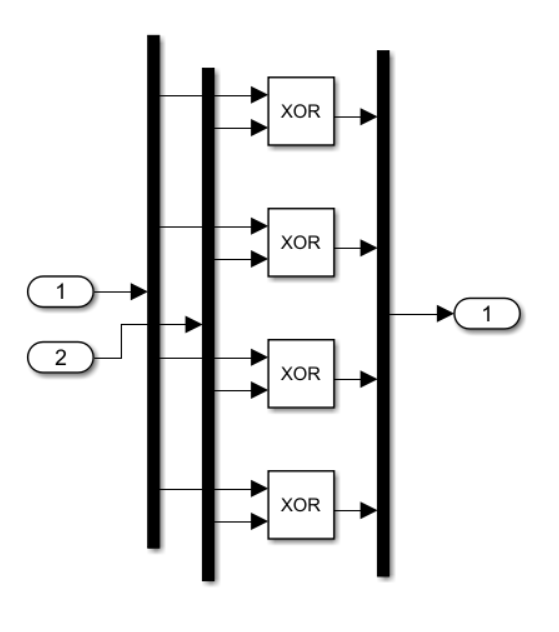
На рисунке 5. показана подсистема SUM.
Эта подсистема предназначена для сложения 2-х двоичных чисел.
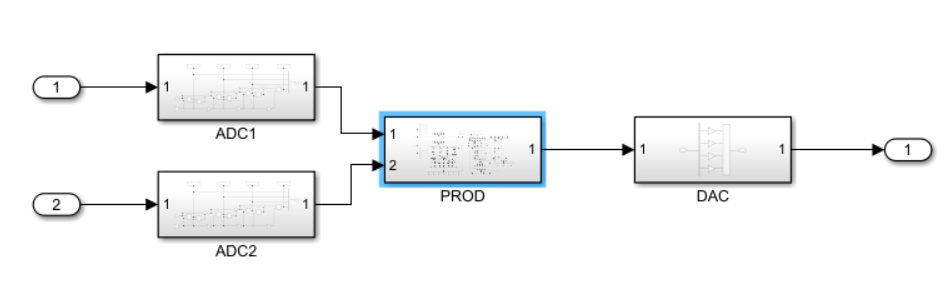
На рисунке 6. показана подсистема PROD_1, состоящая из 2 подсистем ADC, подсистемы PROD и подсистемы DAC.
В этой подсистеме мы используем подсистему ADC для преобразования числа в двоичный код и подсистему PROD для вычисления умножения двух чисел. И, наконец, подсистема DAC для обратного преобразования в десятичный формат.
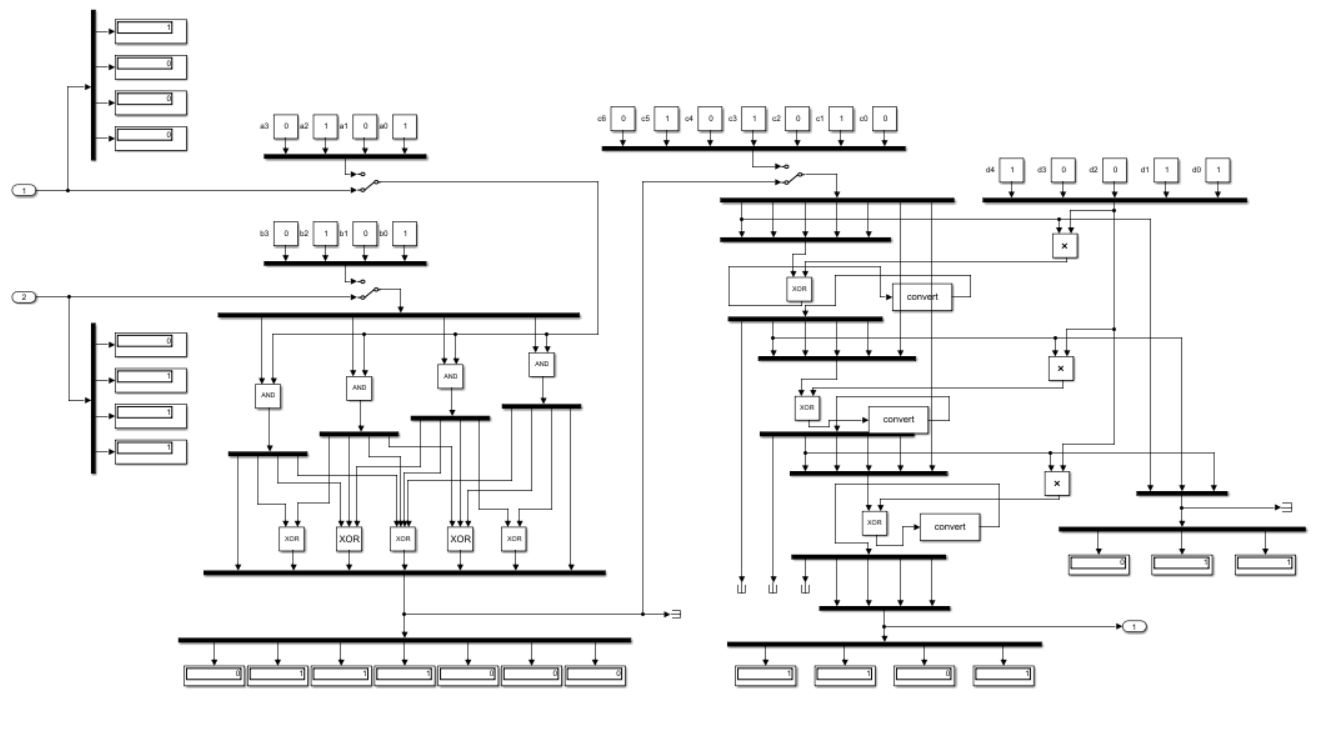
На рисунке 7. показана система PROD подсистема, которая используется для умножения.
В этой подсистеме умножаются 2 двоичных числа, и затем результаты передаются в подсистему DAC для преобразования в десятичные.
Результаты моделирования
На рисунке 7. показана входные данные для модели.
При вводе числа в поле константа для умножения и сложения будут использоваться первое и второе числа.
В этом примере используется следующее число: 5 и 7.
Для сложения мы можем рассчитать вручную, используя сложение по модулю 2.
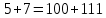
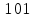
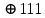
010 = 2
В качестве ответа мы получаем результат 2.
Для умножения мы можем вычисить вручную, используя производящий многочлен.
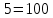
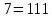
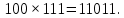
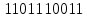
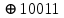
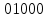=8 Мы получаем ответ = 8.
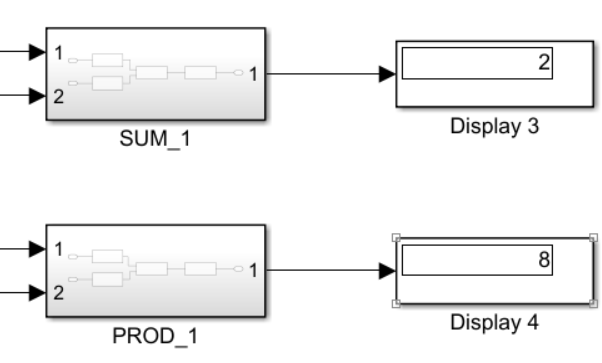
На рисунке 9. показана результат, полученный с помощью модели.
Сравнивая результат с моделью в MATLAB, мы видим, что ответ тот же. это показывает, что модель работает и может быть использована при вычислении чисел с помощью поля Galios.
Cписок литературы
-
Полиноминальная арифметика и поля Гаула или информация, возкресшая из пепла II. https://konyakov.ru/pubs/books/kris-kaspersky-r_i_p/kris-kaspersky07.pdf?ysclid=lihk99906d366387248, Крис Касперски, 2003 год.
-
Поле Галуа в криптографии. https://sites.math.washington.edu/morrow/336_12/papers/juan.pdf, Кристофорус Хуан Бенвенуто, 2012 год.
-
Aрифметика двоичного поля Галуа на базе быстрого умножения и инвертирования элементов поля и ее аппаратная реализация. https://applied-research.ru/ru/article/view?id=7942, Рахман П.А., 2015 год.