Файл: Отчет по учебной маркшейдерской практике преподаватель Юнаков Ю. Л. подпись, дата инициалы, фамилия.docx
Добавлен: 09.11.2023
Просмотров: 884
Скачиваний: 19
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1 Эксплуатационные поверки инструментов
1.1 Поверки и юстировки теодолита
1.2 Поверки и юстировки нивелира
3 Измерение горизонтальных углов
5.1 Прямая геодезическая засечка
5.2 Обратная геодезическая засечка
7.1 Тригонометрическое нивелирование по горным выработкам
7.2 Геометрическое нивелирование
7.3 Нивелирование рельсовых путей
5.1 Прямая геодезическая засечка
Применяется для определения координат дополнительной точки на основании двух исходных пунктов с известными координатами на местности, неудобной для производства линейных измерений. Для этого достаточно, установив теодолит последовательно на исходных пунктах А и В измерить горизонтальные углы
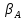 и
и 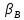 между исходной стороной АВ и направлениями на определяемую точку.
между исходной стороной АВ и направлениями на определяемую точку.Прямая засечка может быть использована также для привязки теодолитных или тахеометрических ходов к пунктам геодезической опорной сети, для чего необходимо измерить дополнительно примычный угол
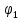 (или
(или 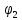 ) на определяемой точке.
) на определяемой точке.Были даны координаты точки А (605,308; 550,510) и В (654,020; 584,936) измерены горизонтальные углы
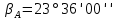 и
и 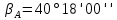 (рис. 5). Нужно было найти координаты точки С (
(рис. 5). Нужно было найти координаты точки С (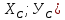 .
.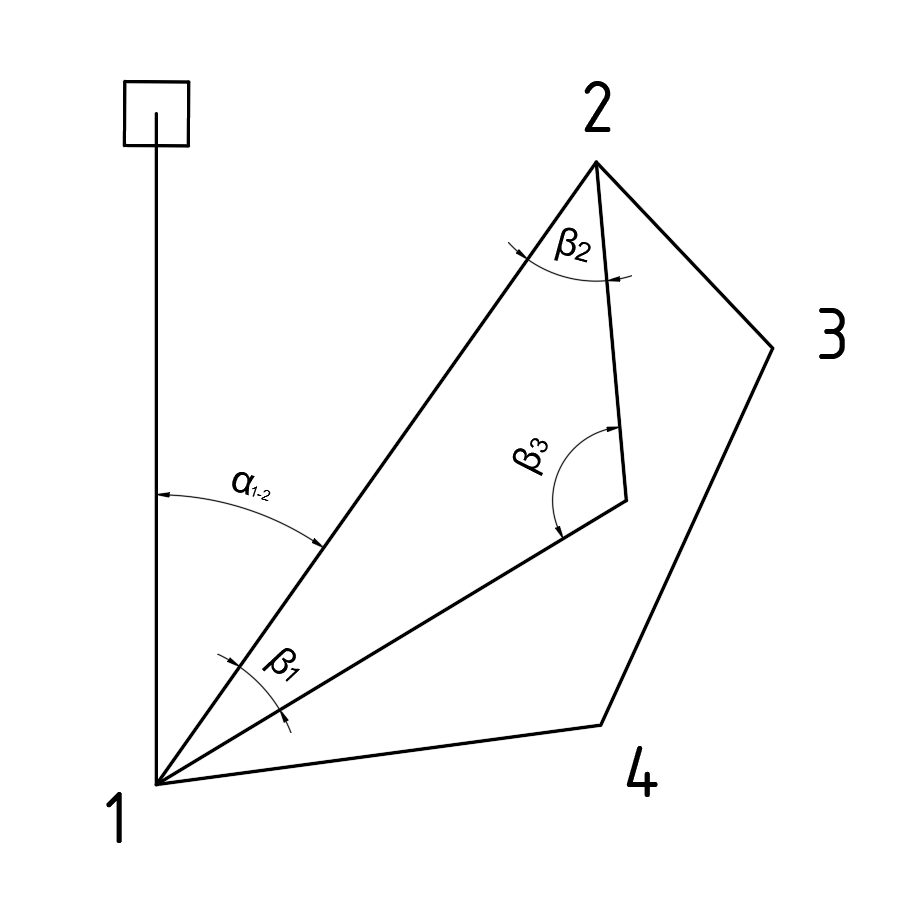
Рисунок 5 – Прямая геодезическая засечка
1. Вычислили горизонтальный угол
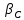 .
.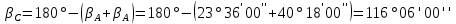
2. Определили дирекционный угол
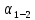 , а также длину стороны АВ.
, а также длину стороны АВ.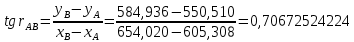
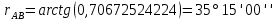
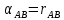 , т.к.
, т.к. 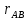 находится в I четверти.
находится в I четверти.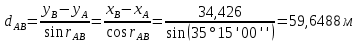
3. Определили длины других сторон треугольника.
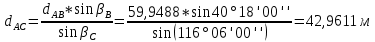
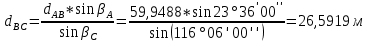
4. Нашли дирекционные углы
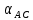 и
и 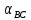 .
.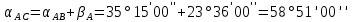
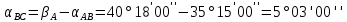
5. Вычислили приращения координат точки С.
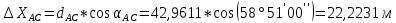
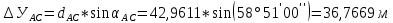
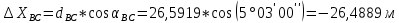
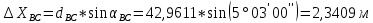
6. Нашли координаты искомой точки С.
А:
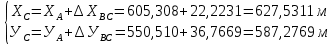
В:
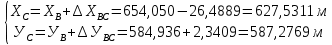
5.2 Обратная геодезическая засечка
Заключается в определении координат дополнительной точки М путём измерения на этой точке углов (
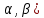 между направлениями на три данных пункта и более с известными координатами.
между направлениями на три данных пункта и более с известными координатами.При использовании обратной засечки для привязки теодолитных или тахеометрических ходов к пунктам геодезической опорной сети необходимо измерить дополнительно примычный угол
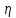 на определяемой точке.
на определяемой точке.Были даны координаты пунктов А (609,946; 585,283), В (605,308; 550,510) и С (654,020; 584,936), измерены горизонтальные углы
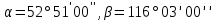 (рис. 6). Необходимо было найти координаты точки М
(рис. 6). Необходимо было найти координаты точки М 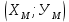 .
.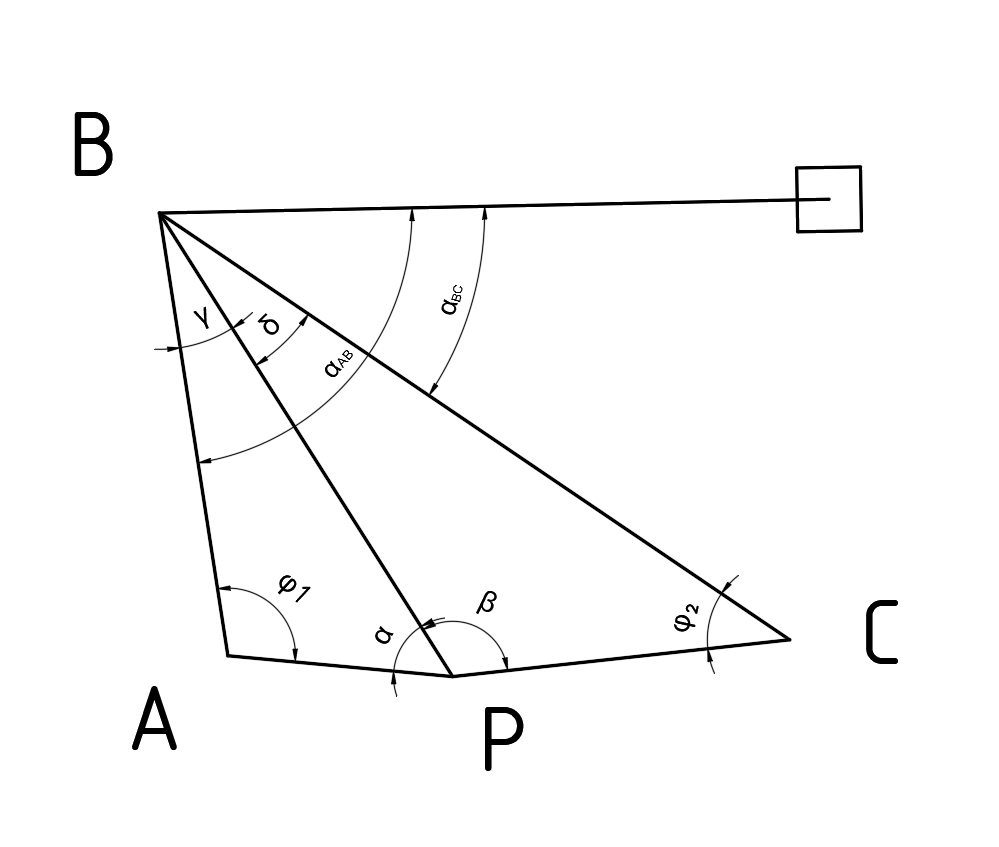
Рисунок 6 – Обратная геодезическая засечка
1. Нашли дирекционные углы
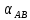 и
и 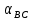 и горизонтальные длины c и d.
и горизонтальные длины c и d.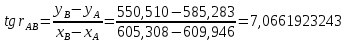
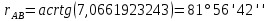
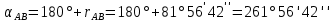 , т.к. III четверть.
, т.к. III четверть.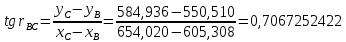
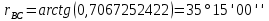
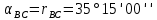 , т.к. I четверть.
, т.к. I четверть.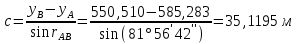
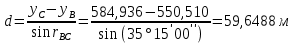
2. Вычислили значение угла ABC.
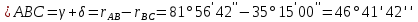
3. Определили горизонтальные углы
 и
и  .
.а) Нашли сумму углов
 и
и  .
.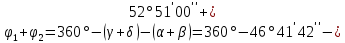
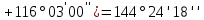
б) Определили разность углов
 и
и  .
.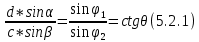
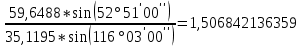
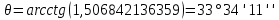
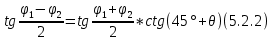
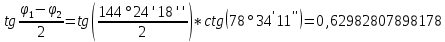
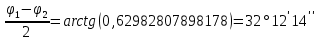
в) Нашли значения углов
 и
и  .
.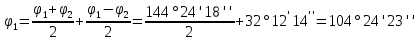
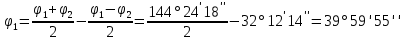
4. Определили углы
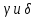 .
.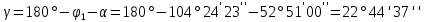
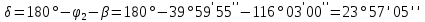
Контроль:
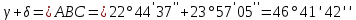
5. Нашли дирекционные углы AM и CM и горизонтальные длины этих сторон
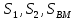 .
.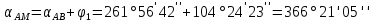
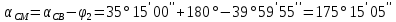
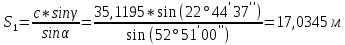
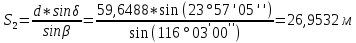
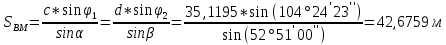
6. Вычислили приращение координат точки M:
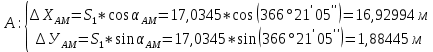
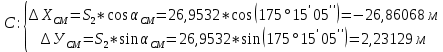
7. Вычислили координаты искомой точки M дважды:
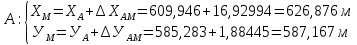
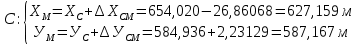
6 Вынос точки на местность
На плане горных работ координаты точки не заданы, поэтому нашли эту точку графическим способом.
Этот способ применяется, когда нужно вычертить координатную сетку с небольшим числом квадратов. Число квадратов по оси х и у определялись по следующим формулам:
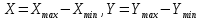
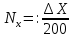
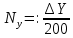
где Xmax, Ymax максимальные значения координат точек, округленные в большую сторону до величин, кратных длине квадрата в данном масштабе. Xmin, Ymin минимальные значения координат, округленные в меньшую сторону до величин, кратных длине квадрата сетки в данном масштабе.
Проводят диагонали AB и CD. Из точки пересечения диагоналей (точка O) сделали засечки одинакового размера. Полученные точки a, c, b, d соединили прямыми линиями. Стороны прямоугольника acbd разделили пополам и через точки деления провели прямые 1-2, 3-4, которые должны пройти через точку O пересечения диагоналей. В нашем случае число квадратов нечетное, значит от точек 1,2,3,4 вначале в обе стороны отложили отрезки по 5 см, а затем – по 10 см.
Координатную сетку подписали в соответствии с координатами точек теодолитного хода. Для этого взяли минимальное и максимальное значения X и Y, которые использовались для нахождения числа квадратов сетки по осям X и Y. У нижней горизонтальной линии сетки слева от крайней вертикальной линии подписали минимальное значение абсциссы сбоку самой верхней горизонтальной линии – максимальное значение Х. Аналогично подписали вертикальные линии (ординаты).
Затем нанесли по координатам точки теодолитного хода и проверили правильность нанесения вершин теодолитного хода.
Правильность вершин теодолитного хода проверяют:
- по дирекционным углам
-по внутренним углам при вершинах теодолитного хода.
Подготовка исходных данных для выноса точки
Нанесение точек на план теодолитного хода произвели по их вычисленным углам и проложениям.