Задача 1. Расчет многопролетной шарнирной балки

Дано: l₁=8,4м, F₁=60кН, схема 1, q₁=20кН/м, сечения 2,12, l₂=6,4м, F₂=24кН, q₂=15кН/м, l₃=10,2м, а=1,2м, b=2,1м, М=22кНм.
Расчет статически определимой балки( многопролетной шарнирно-разрезной балки).

1. 
   В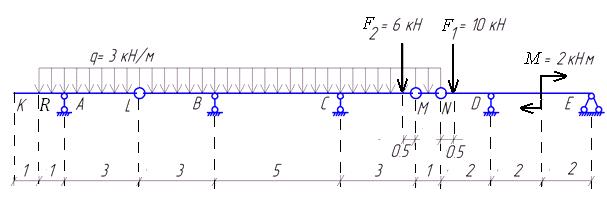
   ычерчиваем балку в масштабе. Прикладываем заданную внешнюю нагрузку. Рассчитать заданную балку, изображенную на рисунке 1.1, на подвижную и неподвижную нагрузки.
   

1. 
   
   

2. 
   П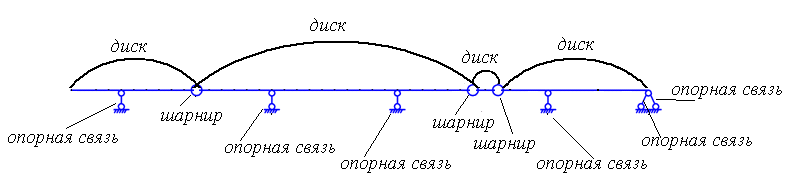
   роверяем выполнение необходимого условия геометрической неизменяемости и статической определимости балки по формуле 1.1.
   

2. 
   
   

В заданной системе 4 диска, 3 шарнира и 6 опорных связей (рисунок 1.2). Отсюда следует, что степень свободы системы равна:



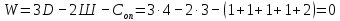
Необходимое условие выполнено. Аналитическое условие 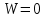является необходимым условием геометрической неизменяемости и показывает, что система является статически определимой.

Составим «поэтажную» схему взаимодействия элементов балки, для проверки достаточного условия геометрической неизменяемости системы (рисунок 1.3). Из схемы видно, что шарниры расположены правильно, следовательно, каждый этаж балки в этой схеме представляет собой статически определимую и геометрически неизменяемую систему. Таким образом, выполнено и достаточное условие геометрической неизменяемости.

В
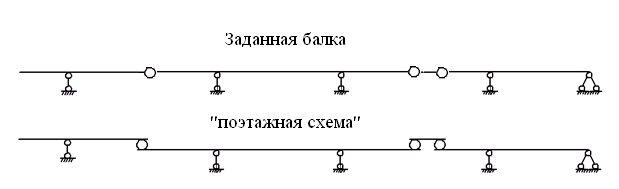
ывод: Так как выполнено и необходимое, и достаточное условия геометрической неизменяемости, то заданная система является геометрически неизменяемой системой. Система статически определима.

3. 
   
   

3. 
   Расчет многопролетной балки производим с помощью поэтажной схемы, начиная с самых верхних этажей, постепенно переходя на нижние этажи, учитывая при этом давление верхних этажей.
   

---

Расчет начинаем с балок KL и MN (верхние этажи).

Расчет балки KL (рисунок 1.4 а).

а) Определение опорных реакций.

,

,

,

.

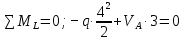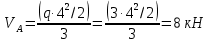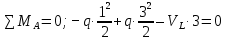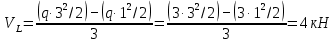б) Определение поперечных сил в характерных точках.

,

,

,





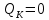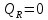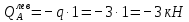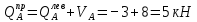
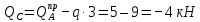
Из уравнения определим точку, в которой поперечная сила равна нулю:



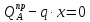
Откуда

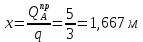
По полученным данным строим эпюру поперечных сил Q (рисунок 1.4 б).

в) Определяем изгибающие моменты в характерных точках.

,

,

,

.

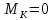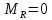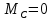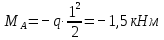В сечении, где Q = 0 на эпюре моментов будет экстремум (x = 1,667 м):



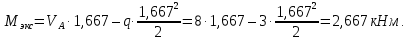
По полученным данным строим эпюру моментов М (рисунок 1.4 в).

Расчет балки MN(рисунок 1.4 г)

а) Определение опорных реакций.









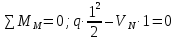
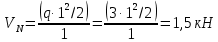
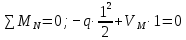
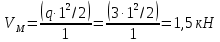
б) Определение поперечных сил в характерных точках.

---

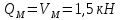
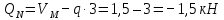
Поперечная сила равна нулю на середине участка.

По полученным данным строим эпюру Q (рисунок 1.4 д).

в) Определение изгибающих моментов в характерных точках.

,



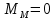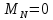
Максимальный момент будет в точке, где поперечная сила равна нулю (x = 0,5 м):



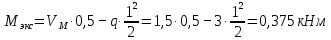
По полученным данным строим эпюру М (рисунок 1.4 е).

Рассчитываем балки нижележащих этажей с учетом опорных реакций, опирающихся на них балок.

Расчет балки LM (рисунок 1.4 ж).

К рассматриваемой балке, помимо заданной нагрузки q и F₂ , в точке L прикладывается сила 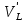и в точке М прикладывается сила .

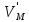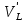представляет давление верхнего этажа KL на нижележащий этаж LM, равное по величине опорной реакции 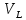вышележащей балки KL в точке опирания L и противоположное по направлению этой реакции.

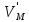представляет давление верхнего этажа MN на нижележащий этаж LM, равное по величине опорной реакции 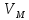вышележащей балки MN в точке опирания M и противоположное по направлению этой реакции.

а) Определение опорных реакций.









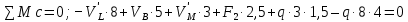
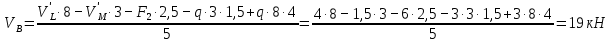
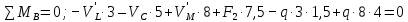
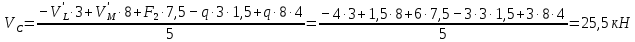
б) Определение поперечных сил в характерных точках балки.

---

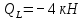
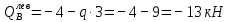
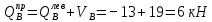
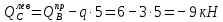
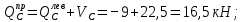
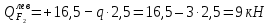
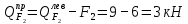
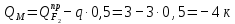Н

Из уравнения определим точку, в которой поперечная сила равна нулю:

,

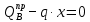откуда

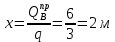
По полученным данным строим эпюру Q (рисунок 1.4 з).

в) Определение изгибающих моментов в характерных точках.











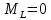
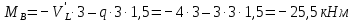
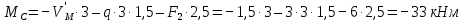
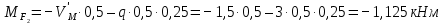
Максимальный момент будет в точке, где поперечная сила равна нулю (x = 2 м):



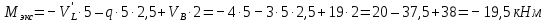
По полученным данным строим эпюру М (рисунок 1.4 и).

Расчет балки NE (рисунок 1.4 к).

К рассматриваемой балке, помимо заданной нагрузки M и F₁ , в точке N прикладывается сила 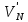. 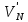представляет давление верхнего этажа MN на нижележащий этаж NE, равное по величине опорной реакции 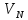вышележащей балки MN в точке опирания N и противоположное по направлению этой реакции.

а) Определение опорных реакций.









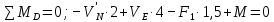
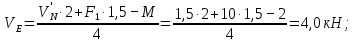
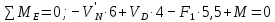
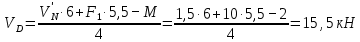
б) Определение поперечных сил в характерных точках балки.

---

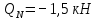
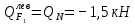
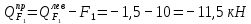
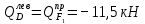
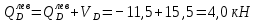
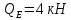
По полученным данным строим эпюру Q (рисунок 1.4 л).

в) Определение изгибающих моментов в характерных точках.













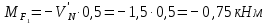
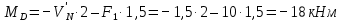
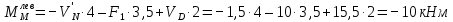
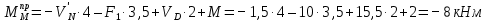
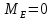
По полученным данным строим эпюру M (рисунок 1.4 м).

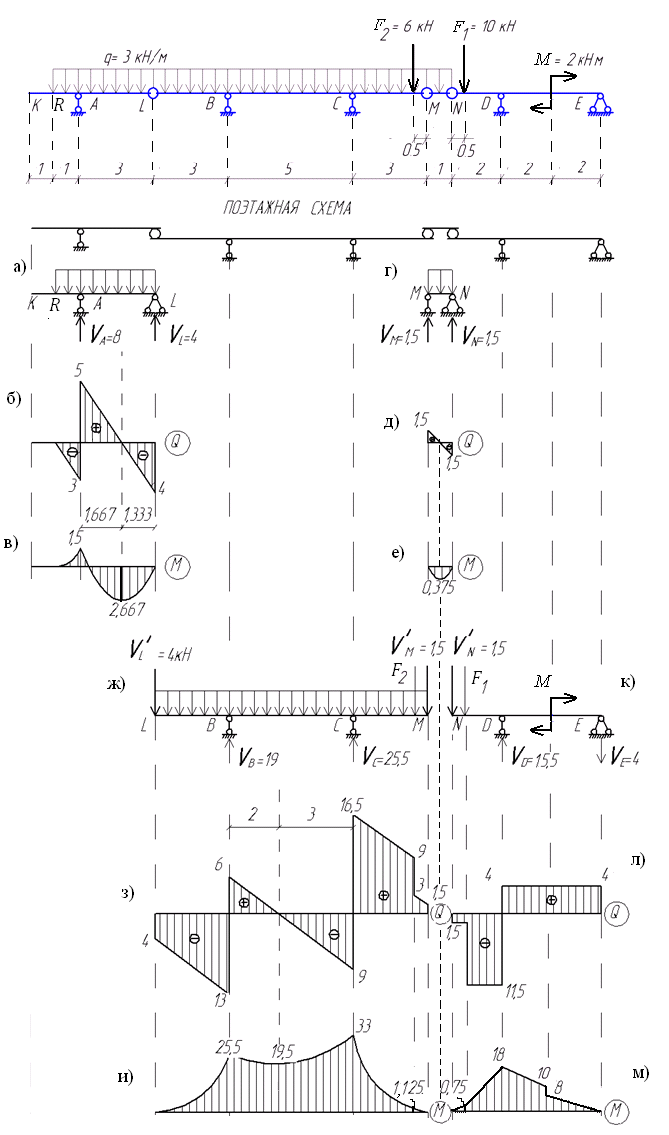
Для того чтобы получить эпюру поперечных сил Q для балки в целом, полученные участки поперечных сил со всех этажей собираем на одну линию (рисунок 1.5 а). Для того чтобы получить эпюру изгибающих моментов М для балки в целом, полученные участки изгибающих моментов со всех этажей собираем на одну линию (рисунок 1.5 б)

4. 
   
   

5. 
   
   

4. 
   Построение линии влияния опорных реакций кинематическим способом:
   

а) Построение линии влияния V_A.

Д
ля этого рассмотрим этаж (участок KL), где находится опора А (рисунок 1.6).

6. 
   
   

Сначала по алгоритму выполняется построение только на выбранном этаже:

• 
  у
  далить вертикальную связь опоры А (рисунок 1.7);
  

7. 
   
   

• 
  
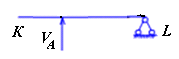
  взамен удаленной связи приложить опорную реакцию V_A (вверх) (рисунок 1.8);
  

8. 
   
   

• 
  с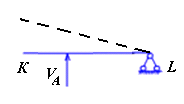
  ообщить возможное перемещение балки в направлении опорной реакции V_A (рисунок 1.9);
  

9. 
   
   

• 
  в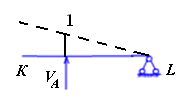
  ыбрать масштаб, приняв ординату линии влияния над опорой А, равную единице (рисунок 1.10).
  

---

Смотрите также файлы

• Измерение временной сложности алгоритма в эксперименте на эвм.docx

• Отчет по лабораторной работе 1 исследование линейных резистивных цепей.docx

• 2 поперечный профиль земляного полотна и его основные элементы 1 Назначение и типы земляного полотна.docx

• Курсовая работа по дисциплине Практические основы бухгалтерского учета источников формирования имущества организации.doc

• Отчет по производственной практике (научноисследовательской работе подготовительный этап).docx