ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.11.2023
Просмотров: 139
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Self-Organizing Feature Maps – SOFM)
Самоорганизующиеся карты Кохонена используются для нахождения групп похожих данных, т.е. в задачах кластеризации, когда целевых векторов нет, а имеются только входные данные. Особенностью сетей Кохонена является то, что в результате обучения нейроны не просто образуют группы схожих данных, но и оказывают взаимодействие друг на друга. Как правило, в основном используются сети Кохонена с двухмерной решеткой, как наиболее удобный способ для восприятия человеком. Чем больше нейронов находится в узлах решетки, тем более детально воспроизводятся особенности анализируемых многомерных данных на двумерную топологическую карту Кохонена.
Сеть Кохонена может иметь один из следующих видов топологий (расположение нейронов):
– gridtop (квадратная решетка),
– hextop (гексагональная решетка),
– randtop (случайная решетка).
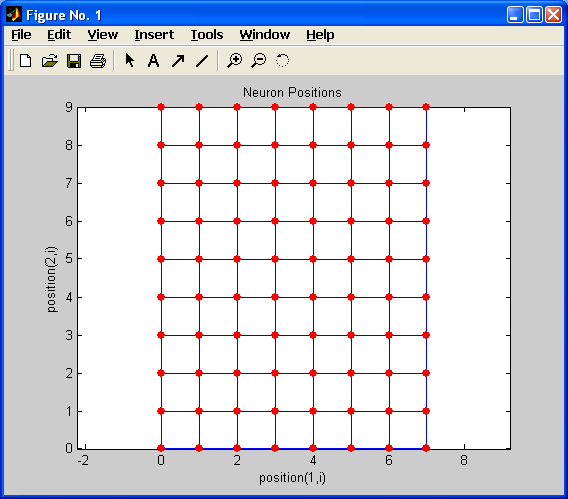
Для визуализации сети Кохонена используется функция plotsom, имеющая в качестве аргумента координаты нейронов. Чтобы получить координаты, необходимо использовать одну из трех топологий. Например, сеть Кохонена с топологией gridtop и количеством нейронов 8x10, можно быть выведена на экран с помощью следующих функций:
pos = gridtop(8,10);
plotsom(pos)
Сеть Кохонена с такими параметрами изображена ниже на рисунке:
Также имеется несколько алгоритмов вычисления расстояний между нейронами: dist, boxdist, linkdist, mandist. Данные функции имеют только один входной аргумент – координаты нейронов. Тогда, например, для сети с гексагональной топологией 2x3, манхэттенское расстояние (или расстояние городских кварталов) вычисляется следующим образом:
pos = hextop(2,3);
a=mandist(pos)
В результате вычисляется матрица размерностью QxQ, где Q – общее количество нейронов (в данном примере Q = 2x3 = 6):
a =
0 1.0000 1.3660 2.3660 1.7321 2.7321
1.0000 0 1.3660 1.3660 2.7321 1.7321
1.3660 1.3660 0 1.0000 1.3660 1.3660
2.3660 1.3660 1.0000 0 2.3660 1.3660
1.7321 2.7321 1.3660 2.3660 0 1.0000
2.7321 1.7321 1.3660 1.3660 1.0000 0
Например, для определения расстояния между 2 и 4 нейронами, необходимо ввести в командное окно MATLAB: a(2, 4). Тогда получим расстояние, равное 1.3660.
Для создания самоорганизующейся сети Кохонена используется функция newsom.
Синтаксис:
net = newsom(PR,[D1,D2,...],TFCN,DFCN,OLR,OSTEPS,TLR,TND)
Входные аргументы
:
PR – массив размера Rx2 минимальных и максимальных значений для R входов;
Di – размер i-ого измерения решетки, по умолчанию = [5 8];
TFCN – топологическая функция, по умолчанию = 'hextop'.
DFCN – функция расстояния, по умолчанию = 'linkdist'.
OLR – значение параметра обучения на начальной фазе, по умолчанию=0.9.
OSTEPS – количество шагов на начальной фазе, по умолчанию = 1000.
TLR – значение параметра обучения на конечной фазе, по умолчанию=0.02;
TND – расстояние до соседнего нейрона на конечной фазе, по умолчанию=1.
Выходные аргументы:
net – объект класса network object.
Пример:
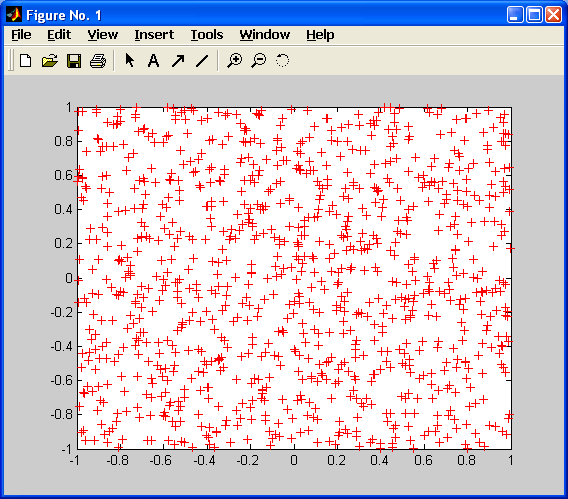
Пусть имеется 1000 двухэлементных векторов, равномерно распределенных в двухмерном пространстве:
P = rands(2,1000);
plot(P(1,:),P(2,:),'+r')
Для того, чтобы выполнить кластеризацию исходных данных, создадим сеть Кохонена размерностью 5x6 с топологией hextop и функцией расстояния linkdist. Т.к. значения данные находятся в диапазоне от -1 до 1, тогда:
net = newsom([-1 1; -1 1],[5 6]);
Можно визуализировать полученную сеть с помощью функции plotsom:
plotsom(net.iw{1,1},net.layers{1}.distances), где net.iw{1,1} – матрица весов сети Кохонена; net.layers{1}.distances – матрица расстояний меду нейронами.
Сеть Кохонена до обучения изображена на рисунке ниже:
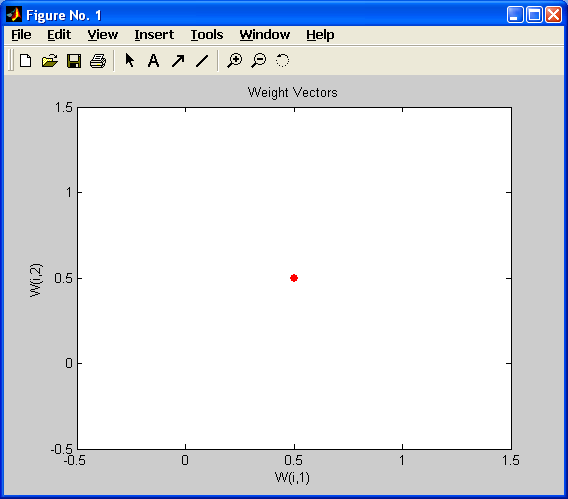
Перед обучением веса сети Кохонена вычисляются как средние величины между минимальными и максимальными значениями матрицы PR, которая задается в качестве первого аргумента функции newsom.
Для обучения сети Кохонена необходимо задать количество эпох обучения. Например, в связи с большим набором данных установим этот параметр равным пяти:
net.trainParam.epochs = 5;
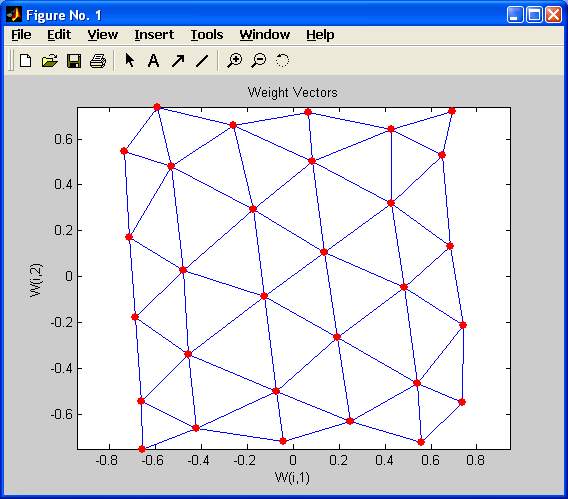
Обучение сети производится с помощью функции train:
net = train(net,P);
plotsom(net.iw{1,1},net.layers{1}.distances)
Теперь после обучения можно использовать функцию тестирования нейронной сети sim. Например, зададим двухэлементный вектор h, для которого необходимо определить, к какому нейрону (классу) он относится:
h = [0.5;0.3];
Определим какой нейрон “победил” для данного вектора:
a = sim(net, h)
Тогда, получим результат, указывающий на принадлежность исследуемого вектора к 16 нейрону (классу)
a = (16,1) 1
Задание.
1. Загрузить в рабочее пространство MATLAB данные о так называемых ирисах Фишера. Для каждого экземпляра ириса известны 4 величины: длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка. Входной файл meas состоит из 150 строк (по 50 для каждого сорта). Задача состоит в разбиении данных на три группы. Команда
load позволяет загружать файлы с данными в рабочее пространство MATLAB:
load fisheriris;
meas=meas'; (транспонирование матрицы для корректной работы нейросети)
2. Создать самоорганизующуюся сеть Кохонена с любой топологией (например, hextop с размерностью 1x3) и любой функцией расстояния (dist, boxdist, linkdist или mandist). Для определения минимальных и максимальных значений необходимо использовать функцию minmax:
minmax(meas);
3. Установить необходимое количество эпох обучения.
4. Определить отклики нейронной сети для всех данных (т.е. для всех экземпляров ириса).
5. Полученные значения откликов (номера классов принадлежности каждого экземпляра ириса) проанализировать с целью определения эффективности кластеризации данных. Для этого следует использовать файл species, который содержит название вида для каждого экземпляра ириса (setosa, versicolor, virginica). Также необходимо подтвердить или опровергнуть предположение, что класс versicolor является гибридом классов setosa и virginica.
1. Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6. – М.: ДИАЛОГ-МИФИ, 2002. – 496 с. ,
2. Потемкин В.Г. Инструментальные средства MATLAB 5.x. М.: Диалог-МИФИ, 2000. – 336 с.
3. Лазарев Ю.Ф. MATLAB 5.x. Киев: Издат. группа BHV, 2000. –384 с.
4. Мишулина О.А., Лабинская А.А., Щербинина М.В. Лабораторный практикум по курсу "Введение в теорию нейронных сетей". М.: МИФИ, 2000. – 204 с.
5. Галушкин А.И. Теория нейронных сетей. М.: ИПРЖР, 2000. – 416 с.
Самоорганизующиеся карты Кохонена используются для нахождения групп похожих данных, т.е. в задачах кластеризации, когда целевых векторов нет, а имеются только входные данные. Особенностью сетей Кохонена является то, что в результате обучения нейроны не просто образуют группы схожих данных, но и оказывают взаимодействие друг на друга. Как правило, в основном используются сети Кохонена с двухмерной решеткой, как наиболее удобный способ для восприятия человеком. Чем больше нейронов находится в узлах решетки, тем более детально воспроизводятся особенности анализируемых многомерных данных на двумерную топологическую карту Кохонена.
Сеть Кохонена может иметь один из следующих видов топологий (расположение нейронов):
– gridtop (квадратная решетка),
– hextop (гексагональная решетка),
– randtop (случайная решетка).
Для визуализации сети Кохонена используется функция plotsom, имеющая в качестве аргумента координаты нейронов. Чтобы получить координаты, необходимо использовать одну из трех топологий. Например, сеть Кохонена с топологией gridtop и количеством нейронов 8x10, можно быть выведена на экран с помощью следующих функций:
pos = gridtop(8,10);
plotsom(pos)
Сеть Кохонена с такими параметрами изображена ниже на рисунке:

Также имеется несколько алгоритмов вычисления расстояний между нейронами: dist, boxdist, linkdist, mandist. Данные функции имеют только один входной аргумент – координаты нейронов. Тогда, например, для сети с гексагональной топологией 2x3, манхэттенское расстояние (или расстояние городских кварталов) вычисляется следующим образом:
pos = hextop(2,3);
a=mandist(pos)
В результате вычисляется матрица размерностью QxQ, где Q – общее количество нейронов (в данном примере Q = 2x3 = 6):
a =
0 1.0000 1.3660 2.3660 1.7321 2.7321
1.0000 0 1.3660 1.3660 2.7321 1.7321
1.3660 1.3660 0 1.0000 1.3660 1.3660
2.3660 1.3660 1.0000 0 2.3660 1.3660
1.7321 2.7321 1.3660 2.3660 0 1.0000
2.7321 1.7321 1.3660 1.3660 1.0000 0
Например, для определения расстояния между 2 и 4 нейронами, необходимо ввести в командное окно MATLAB: a(2, 4). Тогда получим расстояние, равное 1.3660.
Для создания самоорганизующейся сети Кохонена используется функция newsom.
Синтаксис:
net = newsom(PR,[D1,D2,...],TFCN,DFCN,OLR,OSTEPS,TLR,TND)
Входные аргументы
:
PR – массив размера Rx2 минимальных и максимальных значений для R входов;
Di – размер i-ого измерения решетки, по умолчанию = [5 8];
TFCN – топологическая функция, по умолчанию = 'hextop'.
DFCN – функция расстояния, по умолчанию = 'linkdist'.
OLR – значение параметра обучения на начальной фазе, по умолчанию=0.9.
OSTEPS – количество шагов на начальной фазе, по умолчанию = 1000.
TLR – значение параметра обучения на конечной фазе, по умолчанию=0.02;
TND – расстояние до соседнего нейрона на конечной фазе, по умолчанию=1.
Выходные аргументы:
net – объект класса network object.
Пример:
Пусть имеется 1000 двухэлементных векторов, равномерно распределенных в двухмерном пространстве:
P = rands(2,1000);
plot(P(1,:),P(2,:),'+r')

Для того, чтобы выполнить кластеризацию исходных данных, создадим сеть Кохонена размерностью 5x6 с топологией hextop и функцией расстояния linkdist. Т.к. значения данные находятся в диапазоне от -1 до 1, тогда:
net = newsom([-1 1; -1 1],[5 6]);
Можно визуализировать полученную сеть с помощью функции plotsom:
plotsom(net.iw{1,1},net.layers{1}.distances), где net.iw{1,1} – матрица весов сети Кохонена; net.layers{1}.distances – матрица расстояний меду нейронами.
Сеть Кохонена до обучения изображена на рисунке ниже:

Перед обучением веса сети Кохонена вычисляются как средние величины между минимальными и максимальными значениями матрицы PR, которая задается в качестве первого аргумента функции newsom.
Для обучения сети Кохонена необходимо задать количество эпох обучения. Например, в связи с большим набором данных установим этот параметр равным пяти:
net.trainParam.epochs = 5;
Обучение сети производится с помощью функции train:
net = train(net,P);
plotsom(net.iw{1,1},net.layers{1}.distances)

Теперь после обучения можно использовать функцию тестирования нейронной сети sim. Например, зададим двухэлементный вектор h, для которого необходимо определить, к какому нейрону (классу) он относится:
h = [0.5;0.3];
Определим какой нейрон “победил” для данного вектора:
a = sim(net, h)
Тогда, получим результат, указывающий на принадлежность исследуемого вектора к 16 нейрону (классу)
a = (16,1) 1
Задание.
1. Загрузить в рабочее пространство MATLAB данные о так называемых ирисах Фишера. Для каждого экземпляра ириса известны 4 величины: длина чашелистика, ширина чашелистика, длина лепестка, ширина лепестка. Входной файл meas состоит из 150 строк (по 50 для каждого сорта). Задача состоит в разбиении данных на три группы. Команда
load позволяет загружать файлы с данными в рабочее пространство MATLAB:
load fisheriris;
meas=meas'; (транспонирование матрицы для корректной работы нейросети)
2. Создать самоорганизующуюся сеть Кохонена с любой топологией (например, hextop с размерностью 1x3) и любой функцией расстояния (dist, boxdist, linkdist или mandist). Для определения минимальных и максимальных значений необходимо использовать функцию minmax:
minmax(meas);
3. Установить необходимое количество эпох обучения.
4. Определить отклики нейронной сети для всех данных (т.е. для всех экземпляров ириса).
5. Полученные значения откликов (номера классов принадлежности каждого экземпляра ириса) проанализировать с целью определения эффективности кластеризации данных. Для этого следует использовать файл species, который содержит название вида для каждого экземпляра ириса (setosa, versicolor, virginica). Также необходимо подтвердить или опровергнуть предположение, что класс versicolor является гибридом классов setosa и virginica.
Список используемой литературы:
1. Медведев В.С., Потемкин В.Г. Нейронные сети. MATLAB 6. – М.: ДИАЛОГ-МИФИ, 2002. – 496 с. ,
2. Потемкин В.Г. Инструментальные средства MATLAB 5.x. М.: Диалог-МИФИ, 2000. – 336 с.
3. Лазарев Ю.Ф. MATLAB 5.x. Киев: Издат. группа BHV, 2000. –384 с.
4. Мишулина О.А., Лабинская А.А., Щербинина М.В. Лабораторный практикум по курсу "Введение в теорию нейронных сетей". М.: МИФИ, 2000. – 204 с.
5. Галушкин А.И. Теория нейронных сетей. М.: ИПРЖР, 2000. – 416 с.