Файл: Нейронные сети в matlab.doc

Для просмотра и установки весов и смещений используются, соответственно, функции net.IW{i} и net.b{i}, где i – номер нейрона, для которого устанавливаются веса или смещение.

Адаптация персептрона осуществляется с помощью функции adapt.

Синтаксис:

net = adapt(net, P,T)

где net – адаптируемая нейронная сеть,

P – последовательность векторов входа,

T – последовательность целей.

Число проходов адаптации устанавливается следующим образом:

net.adaptParam.passes = n;

где n – число проходов адаптации.

Моделирование персептрона осуществляется с помощью функции sim.

Синтаксис:

Y = sim(net,P)

где net – моделируемая нейронная сеть,

P – последовательность векторов входа,

Y – последовательность результатов.
Задание.
1. Создать в рабочем пространстве MATLAB персептрон и просмотреть его структуру с помощью функции gensim(net).

2. Обучить персептрон выполнению одной из логических операций и промоделировать его.

Последовательность векторов входа подготовить в виде:

P = {[0; 0] [0;1] [1;0] [1;1]};

Последовательность целей подготовить в виде, например (для операции И):

p={[0;0] [0;1] [1;0] [1;1]};

преобразуем матрицу входа p к другому виду:

p1=cat(2, p{:});

Получим выход для И:

T1=num2cell(p1(1,:) & p1(2,:))

В итоге на экране:

T1 = {[0] [0] [0] [1]};

3. Настроить параметры персептрона для выполнения логической функции AND, используя процедуру адаптации:

net.adaptParam.passes = 10; – число проходов

net.adapt(net,p,T1); – настройка на AND;

Зададим веса и смещения для И:

net.IW{1,1}=[2;1]

net.b{1}=-3

Получим выход:

Y =sim(net,p)

Сравните значение Y c Т1.

По аналогии обучите нейрон операции логического или. При этом используйте вместо Т1 – Т2= num2cell(p1(1,:) | p1(2,:))

И установите веса и смещения, равными:

net.IW{1,1}=[2;2]

net.b{1}=-2

Лабораторная работа 6

Сети прямой передачи в рабочем пространстве MATLAB
Для создания многослойных нейронных сетей прямой передачи сигнала используется функция newff.

Синтаксис:

net = newff(PR,[S1 S1…SNI],{TF1 TF2…TFN},btf,blf,pf)

Входные аргументы.

PR – массив размера Rx2 минимальных и максимальных значений для R векторов входа;

Si – количество нейронов в слое i;

Tfi – функция активации слоя i, по умолчанию tansig;

btf – обучающая функция, реализующая метод обратного распространения, по умолчанию trainlm;

blf – функция настройки, реализующая метод обратного распространения, по умолчанию traingdm;

pf – критерий качества обучения, по умолчанию mse.
Выходные аргументы.

---

net – объект класса network object.

Пример. (не реализуется в Matlab, если не зададите свои Р и Т)

net = newff([0 10],[5 1], {'tansig' 'purelin'});

Создается двухслойная нейронная сеть с прямой передачей сигнала; первый слой – 5 нейронов с функцией активации tansig; второй слой – 1 нейрон с функцией активации purelin; диапазон изменения входа [0 10].
Обучение сети осуществляется с помощью функции train.

Синтаксис:

net = train(net, P,T)

где net – обучаемая нейронная сеть,

P – последовательность векторов входа,

T – последовательность целей.

Число эпох обучения устанавливается следующим образом:

net.trainParam.epochs = n;

где n – число эпох обучения.

В процессе обучения автоматически составляется график ошибки сети в зависимости от номера эпохи.
Задание.
1. Создать в рабочем пространстве MATLAB двухслойную нейронную сеть с прямой передачей сигнала; число нейронов на втором слое –1; на первом – варьируется; функции активации – tansig, purelin.

2. Задать последовательности входов и целей. Например:

P = [0 1 2 3 4 5 6 7 8 9 10];

T = [0 1 2 3 4 3 2 1 2 3 4];

3. Выполнить моделирование сети.

Y = sim(net,P);

Построить графики сигналов выхода и цели:

plot(P, T, P, Y, 'o')

4. Обучить сеть в течение, например, 50 циклов.

4. 
   Промоделировать обученную сеть и построить графики.
   

Лабораторная работа 7

Сети Хопфилда

Для создания модифицированной сети Хопфилда используется функция Newhop

Синтаксис:

Net=NewHop(T)

Входной аргумент:

Массив T размера RхQ, объединяющий Q целевых векторов (со значениями +1 или –1). R- число элементов входного вектора
Выходные аргументы:
net – объект класса network object
Пример:
T=[-1 -1 1; 1 -1 1];

net=newhop(T);
Создается сеть Хопфилда с двумя устойчивыми точками в трехмерном пространстве.
Архитектура сети:

Рекуррентная многослойная сеть в которой вход и выход линейного слоя совпадают.
В сети используется линейная функция активации с насыщением Satlins(),

которая описывается следующим образом:




-1, n<-1

n, -1<=n<=1

1, n>1

Сеть Хопфилда может быть промоделирована с одним или большим количеством векторов, которые задаются как начальные условия. После того как начальные условия заданы сеть генерирует выход который по обратной связи подается на вход. Этот процесс повторяется много раз, пока на выходе не установится равновесие.

---

Спроектировать сеть Хопфилда – значит создать рекуррентную сеть со множеством точек равновесия, таких, что при задании начальных условий сеть приходит в состояние покоя в одной из этих точек.
Рассмотрим следующий пример: требуется разработать сеть с двумя устойчивыми точками в вершинах трехмерного куба

T=[-1 -1 1; 1 -1 1]'

Вывод на экран:

T=-1 1

T=-1 -1

T=-1 -1
Выполним синтез сети:
net=newhop(T);

gensim(net);
После создания сети можно получить информацию о ее структуре, используя метод Layers()
net.layers(1);
Далее удостоверимся, что разработанная сеть имеет устойчивые состояния в этих двух точках используя функцию Sim(net,n,[],AI), аргументами которой будут Net – объект типа сеть Хопфилда, N=2- число входных целевых векторов, AI=T-начальное состояние слоя:

AI=T;

[Y,Pf,Af]=sim(net,2,[],AI);

Y

На выходе получим:

Y=-1 1

-1 –1

1 –1

Что соответствует точкам равновесия.

Если теперь мы зададим другой начальный массив точек, например

AI=[-0.9; -0.8; -0.7] и вызовем функцию Sim
[Y,Pf,Af]=sim(net, [1 5], [],AI);

то получим выходной вектор Y= (-1,-1, 1) т.е. Сеть из заданного начального состояния вернулась в положение равновесия. Следует обратить внимание, что при втором вызове функции Sim в качестве входного параметра указывается такт дискретности (1) и количество шагов моделирования (5).


Задание.

1. 
   Создать в рабочем пространстве MATLAB сеть Хопфилда с четырмя нейронами (входной массив из четырех векторов) и получить о ней информацию используя метод Net.Layers();
   
2. 
   Исследовать поведение созданной сети, используя функцию Sim(), задавая на входе различные начальные массивы (не менее трех различных массивов).
   
3. 
   Исследовать поведение сети, задавая начальные условия случайным образом с помощью функции Rands(). Вывести результаты на экран функцией Plot()
   

Лабораторная работа 8
Радиальные нейронные сети

(Radial Basis Function Neural Networks – RBF NN)
Основным применением нейронных сетей с радиальной функцией (RBF-сетей) является аппроксимация функций. Такие сети имеют два слоя:

1) скрытый слой нейронов с радиально-симметричной функцией. Это специальный класс функций, характерное свойство которых заключается в том, что отклик функции монотонно убывает с удалением от центральной точки. Типичный пример такой функции  – функция Гаусса, имеющая следующее аналитическое представление:

---

График данной функции изображен ниже:



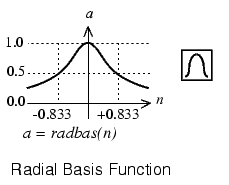
Радиальная функция имеет максимум, равный 1, когда аргумент функции (n) равен нулю. В слое с радиально-симметричной функцией вычисляется расстояние между вектором весов (w) и входным вектором (p). Размерность обоих векторов равна количеству входов рассматриваемого слоя – R. Затем величина расстояния (между w и p) умножается на параметр b(который позволяет задать чувствительность радиального нейрона). Полученное значение и есть аргумент радиальной функции.

Как только расстояние между w и p уменьшается, происходит увеличение значения радиальной функции. Таким образом, радиальный нейрон производит единицу каждый раз, когда вход p идентичен вектору весов w.

Для вычисления радиальной функции используется функция radbas.

Синтаксис:

A = radbas(N)
Входные аргументы:

N – вектор расстояний размера Sx1 для каждого нейрона S.
Выходные аргументы:

A – вектор значений радиальной функции для каждого нейрона S.

Пример:

n = -5:0.1:5;

a = radbas(n);

plot(n,a)
В результате создается график радиальной функции:

2) выходной линейный слой. Данный слой содержит нейроны с линейными функциями. Значение такой функции равно значению ее аргумента. Также каждый нейрон имеет параметр b, который определяет чувствительность нейрона к входным данным.



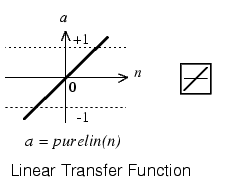
Т.о., RBF-сеть, состоящая из S¹ нейронов в первом слое и S² нейронов во втором слое, схематично представлена на рисунке ниже:



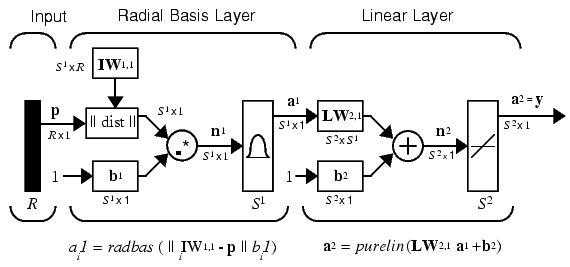
Для создания радиальной нейронной сети используется функция newrb, которая добавляет нейроны в скрытый радиальный слой до тех пор, пока нейронная сеть не удовлетворяет заданному значению ошибки.
Синтаксис:

net = newrb(P,T,GOAL,SPREAD,MN,DF)
Входные аргументы:

P – массив размера RxQ входных векторов, где R – количество входов, Q – количество входных векторов;

T – массив размера SxQ целевых векторов, где R – количество выходов, Q – количество целевых векторов;

---

GOAL – целевая среднеквадратичная ошибка, по умолчанию равна 0;

SPREAD – константа радиальной функции, по умолчанию равна 1;

MN – максимальное число нейронов, по умолчанию равно Q;

DF – количество нейронов, которые необходимо добавлять после каждого вывода ошибки, по умолчанию равно 25.
Выходные аргументы:

net – объект класса network object.
Пример:

Установим входные значения P и связанных с ними выходных значений T (количество значений – 21), а также построим график для этих значений с использованием функций plot, xlabel, ylabel:

P = -1:.1:1;

T = [-.9602 -.5770 -.0729 .3771 .6405 .6600 .4609 ...

.1336 -.2013 -.4344 -.5000 -.3930 -.1647 .0988 ...

.3072 .3960 .3449 .1816 -.0312 -.2189 -.3201];

plot(P,T,'+');

xlabel('Входной вектор P');

ylabel('Целевой вектор T');


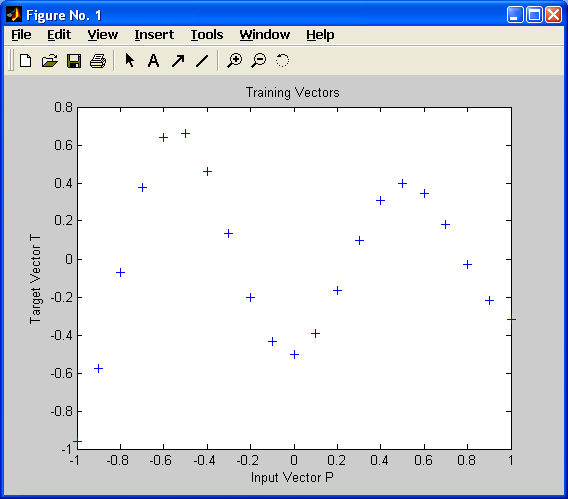
Для того, чтобы найти функцию, проходящую через эти точки, используем следующую команду:

net = newrb(P, T, 0.02, 1);

В результате создается двухслойная радиальная нейронная сеть, которая аппроксимирует данные, заданные векторами P и T. Для сети установлена среднеквадратичная ошибка, равная 0.02, а также параметр spread, равный единице.

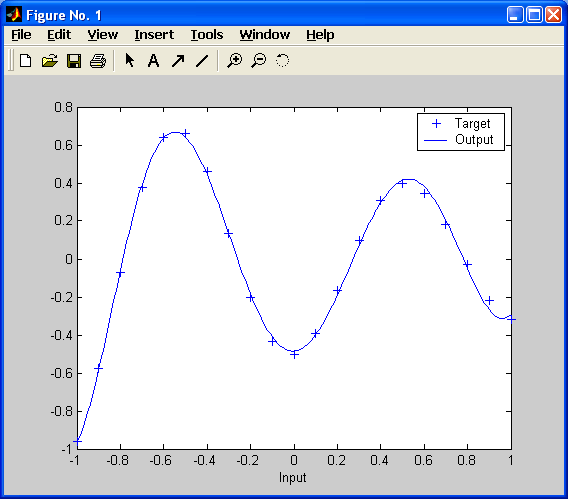
В процессе обучения автоматически составляется график ошибки сети в зависимости от номера эпохи. Чтобы увидеть, насколько точно RBF-сеть аппроксимирует данные, необходимо протестировать сеть и вывести график выходных откликов сети:
plot(P,T,'+');

xlabel('Input');

X = -1:.01:1;

Y = sim(net,X);

hold on;

plot(X,Y);

hold off;

legend({'Target','Output'})


Задание.
1. Задать последовательности входов и целей. Например:

P = [1 2 3 4 5 6 7 8 9 10 11 12];

T = [2.0 4.1 5.9 3.6 1.7 7.3 6.1 9.2 3.8 1.2 4.9 6.3];

2. Создать радиальную нейронную сеть на основе заданных векторов со среднеквадратической ошибкой, равной 0.01. Также установить параметр spread равным единице.

3. Выполнить моделирование сети для новых входов.

Y = sim(net, z), где net – созданная сеть, z – новое входное значение;

4. Построить графики сигналов выхода сети и целевых значений:

plot(P,T,'+');

X = 1:.01:12;

Y = sim(net,X);

hold on;

plot(X,Y);

hold off;

5. Промоделировать обученную сеть при различных значениях параметра spread (например, при 0.3, 0.9, 2, 10, 50 и 100) и построить графики при каждом значении, чтобы сделать вывод о влиянии значения данного параметра на способность RBF-сети выполнять аппроксимацию функций.
Лабораторная работа 9
Самоорганизующиеся карты Кохонена

(

---