Файл: Федеральное агентство морского и речного транспорта фгбоу во гумрф имени адмирала С. О. Макарова.docx
Добавлен: 09.11.2023
Просмотров: 101
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Федеральное агентство морского и речного транспорта
ФГБОУ ВО «ГУМРФ имени адмирала С.О. Макарова»
Котласский филиал
Федерального государственного бюджетного
образовательного учреждения высшего образования
«Государственный университет морского и речного флота
имени адмирала С.О. Макарова»
(Котласский филиал ФГБОУ ВО «ГУМРФ имени адмирала С.О. Макарова»)
Специальность 23.02.03 (Техническое обслуживание и ремонт автомобильного транспорта)
Индивидуальный проект
по учебной дисциплине: Математика
тема: Загадочные графики
Выполнил:
Северьянов М.В., обучающийся гр. 11-АТ
«_______» _______________ 2023г. ____________________
(подпись)
Проверил:
Каданцева О.М., преподаватель
«_______» _______________ 2023г. ____________________
(подпись)
К защите:
Каданцева О.М., преподаватель
«_______» _______________ 2023г. ____________________
(оценка, подпись)
Котлас 2023
Содержание
| Введение | 3 |
| Глава 1. Экстрим и его виды | 4 |
| 1.1 Как возникают экстремальные задачи? | 5 |
| 1.2 Решение практических задач средствами математики | 5 |
| Глава 2. Классическая изопериметрическая задача. Задача Дидоны | 7 |
| Глава 3. Экстремальные задачи в геометрии | 9 |
| Заключение | 11 |
| Литература | 12 |
| Приложение | 13 |
СОДЕРЖАНИЕ
-
Введение -
Теоретическая часть -
Вывод.
Список литературы
Введение
Актуальность: Впервые с тригонометрией я столкнулась в восьмом классе, когда мы начали изучать азы этого раздела математики. Простейшие правила определения синуса и косинуса показались мне очень легкими, поэтому не вызвали особого интереса. Позднее, когда я начал учиться на 1 курсе, то было ясно сразу, что тригонометрия - это огромный раздел математики, объединяющий большое количество знаний и теории. В дальнейшем я выяснил, что знания о тригонометрии очень универсальные для всех областей деятельности. Они имеют широкое применение в астрономии, географии, теории музыки, электронике, теории вероятности, статистике, биологии, медицине, фармацевтике, химии, криптографии и многих других областях.
Термин «тригонометрия» ввел в употребление в 1595 немецкий математик и богослов Варфоломей Питиск, автор учебника по тригонометрии и тригонометрических таблиц. К концу 16 в. большинство тригонометрических функций было уже известно, хотя само это понятия еще не существовало.
Ученые обрабатывали данные измерений, чтобы вести календарь и правильно определять время начала сева и сбора урожая, даты религиозных праздников. По звездам вычисляли местонахождение корабля в море или направление движения каравана в пустыне. Как известно, тригонометрия применяется не только в математике, но и в других сферах науки.
Теоретическая часть
Все тригонометрические функции относятся к основным элементарным функциям. Сейчас мы рассмотрим их графики и перечислим свойства.
Тригонометрическим функциям присуще понятие периодичности (повторяемости значений функции при различных значениях аргумента, отличных друг от друга на величину периода, где Т - период), поэтому, в список свойств тригонометрических функций добавлен пункт «наименьший положительный период». Также для каждой тригонометрической функции мы укажем значения аргумента, при которых соответствующая функция обращается в ноль.
Теперь разберемся со всеми тригонометрическими функциями по-порядку.
Синус
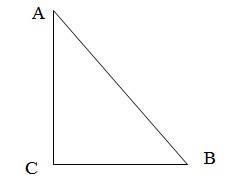
Синус- это тригонометрическая функция, отношение величины
противолежащего катета к величине гипотенузы.
Свойства функции синуса.
Область определения: R (x — любое действительное число) т.е.
Область значений:
Функция нечетная:
Функция периодическая с периодом
Точки пересечения с осями координат:
Промежутки знакопостоянства
Промежутки возрастания и убывания

Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие
их характеристики:
-
область определения; -
область значений; -
четность или нечетность; -
периодичность; -
точки пересечения с осями координат; -
промежутки знакопостоянства; -
промежутки возрастания и убывания; -
наибольшее и наименьшее значения функции.
Абсциссы точек пересечения графика функции с осью Ох (то есть те
значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности
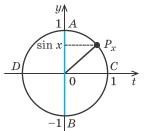
Поскольку ординату можно найти для любой точки единичной окружности
(в силу того, что через любую точку окружности всегда можно провести прямую, перпендикулярную оси координат), то область
— все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату.
Таким образом, для функции область значений:.
Это можно записать так:.
Как видим, наибольшее значение функции sin x равно единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности
является точка A, то есть при
функции
Синус — нечетная функция:
симметричен относительно начала координат.
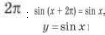 Синус — периодическая функция с наименьшим положительным периодом , таким образом, через промежутки длиной
Синус — периодическая функция с наименьшим положительным периодом , таким образом, через промежутки длиной Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси
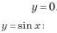 На оси
На оси значения х, при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на
единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства.
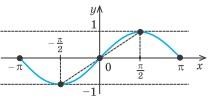
Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях.(рис 2) Таким образом, , а также, учитывая период, при всех
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому

Рис.2 Рис.3
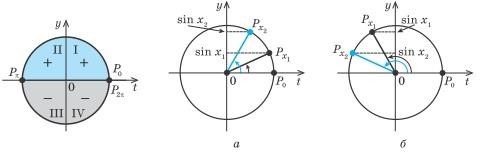
Если (рис.3,б), то при увеличении аргумента ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график
функции
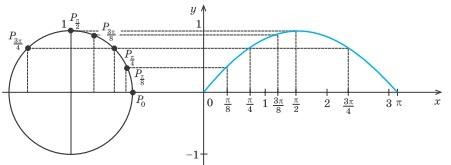 Рис.5
Рис.5