Файл: Федеральное агентство морского и речного транспорта фгбоу во гумрф имени адмирала С. О. Макарова.docx

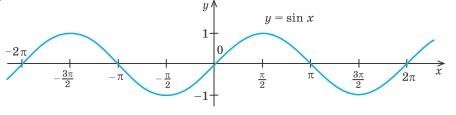
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который

называется синусоидой .(Рис.6)

Геометрические колебания

Колебания - это повторяющийся в той или иной степени вовременипроцесс изменения состояний системы около точкиравновесия. Например, при колебанияхмаятникаповторяются отклонения его в ту и другую сторону от вертикального положения; при колебаниях в электрическом колебательномконтуреповторяются величина и направлениетока, текущего черезкатушку.

Амплитуда – это максимальное значение смещения или изменения переменной величины от среднего значения приколебательномиливолновомдвижении.

Неотрицательнаяскалярнаявеличина, размерность которой совпадает с размерностью определяемой физической величины.

Период – это отрезок времени (или другой величины), определённый меткой

начала отсчёта периода и меткой конца отсчёта периода

Частота – это физическая величина, характеристикапериодическогопроцесса, равна количеству повторений или возникновения событий (процессов) в единицу времени.

Циклическая частота - скалярная величина, являющееся мерой частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. Численно циклическая частота равна числу полных колебаний, совершающихся за 2π единиц времени.

Математический маятник – это осциллятор, представляющий

собой механическую систему, состоящую изматериальной точкина конце невесомой нерастяжимой нити или лёгкогостержняи находящуюся в однородном поле силтяготения

---

Пружинный маятник – это механическая система, состоящая из пружины скоэффициентом упругости(жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

Косинус

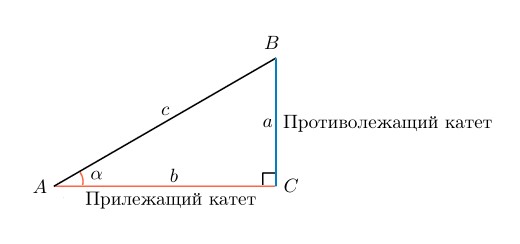
Косинус - это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе.

Свойства косинуса

Область определения функции - множество всех действительных чисел

Множеством значений функции является промежуток

Функция является четной, график симметричен относительно оси Оу.

Функция периодическая. Наименьший положительный период равен

График функции пересекает ось Ох (нули функции) в точках

График функции пересекает ось Оy в точке (0; 1).

Функция принимает положительные	значения на
промежутках Функция принимает отрицательные	значения на

промежутках

Функция возрастает на промежутках

Функция убывает на промежутках

Точки минимума:

Точки максимума:

Графиком функции является косинусоида

---

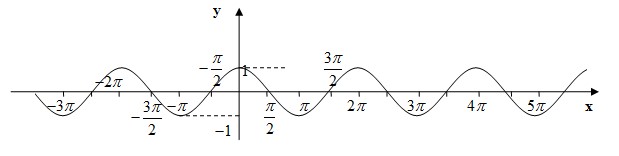
График косинуса

Точно так же, как и в случае синуса, мы можем построить график функции y = cos x. Изображаем на графике информацию с тригонометрического круга. По оси абсцисс — снова угол в радианах, по оси ординат — косинус угла



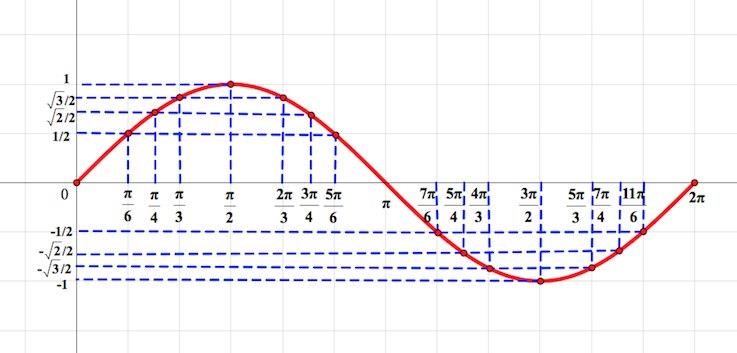
Пунктирная кривая — это график функции y = cos x на промежутке [0; 2π]. График косинуса на всей числовой оси получается периодическим повторением данного фрагмента

Тангенс

Тангенс – это отношение синуса к косинусу (т. е. tg = sin/cos) или отношение противолежащего катета к прилежащему.

Основныесвойства функцииy=tgx:

Область определения функции:

Множеством значений функции:

Функция является нечетной, график симметричен относительно начала координат

(0;0).

Функция периодическая. Наименьший положительный период равен График функции пересекает ось Ох (нули функции) в точках График функции пересекает ось Оy в точке (0; 0).

Функция принимает положительные значения на промежутках

Функция принимает отрицательные значения на промежутках

Функция возрастает на промежутках

Промежутки убывания отсутствуют.

Точек минимума нет.

Точек максимума нет.

Графиком функции является тангенсоида:

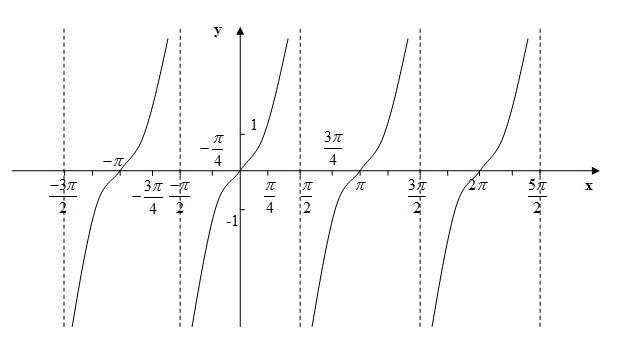
Котангенс

Котангенс – это отношение косинуса к синусу (т. е. ctg = cos/sin) или

отношение прилежащего катета к противолежащему.

Свойства котангенса

Область определения функции:

---

Множеством значений функции:

Функция является нечетной, график симметричен относительно начала координат

(0;0).

Функция периодическая. Наименьший положительный период равен

График функции пересекает ось Ох (нули функции) в точках

Функции не пересекает ось Оy.

Функция принимает положительные значения на промежутках Функция принимает отрицательные значения на промежутках

Функция не имеет промежутков возрастания.

Промежутки убывания:

Точек минимума нет.

Точек максимума нет.

Графиком функции является котангенсоида:

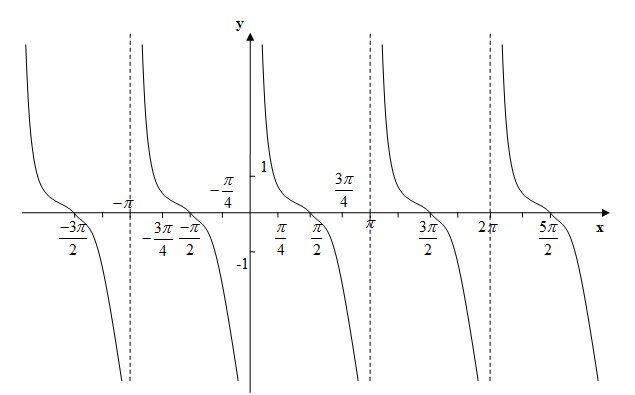
Период функции

1. 
   Если T - основной период функции y=f(x), то число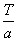 является
   

основным периодом функции y=f(ax), где a - любое положительное число.

2. 
   Если периодические функции y=f(x) и y=g(x) имеют один и тот же период T, то их сумма, разность и произведение тоже будет иметь период T.
   

3. 
   Если периодические функции y=f(x) и y=g(x) имеют соизмеримые периоды T₁ и T₂, то они имеют общий период.
   

4. 
   Период сложной функции y=g(f(x)) совпадает с периодом функции y=f(x).
   

Триангуляция

Примеры практического применения

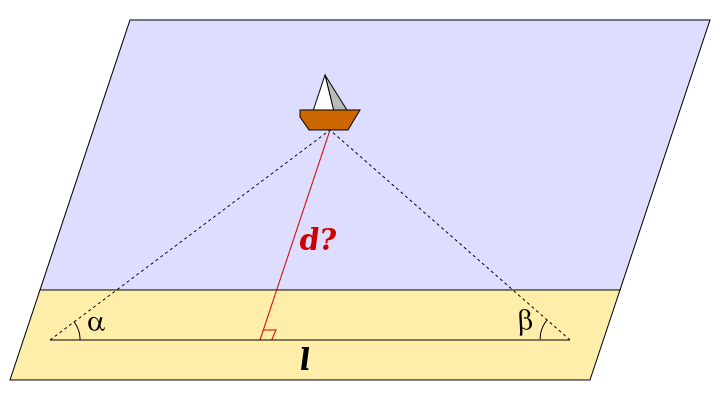
Чтобы определить расстояние d от берега до недоступной точки — например, до удалённого корабля,— нужно отметить на берегу две точки, расстояние

---

l между которыми известно, и измерить углы a и b между линией, соединяющей эти точки, и направлением на корабль. Из формул варианта «сторона и прилежащие к ней углы»можно найти длину высоты треугольника

d= sin(a)* sin(b)/sin(a+b)*l = tg(a)* tg(b)/ tg(a)+tg(b)*l

Сферические теоремы косинусов

Теоремы косинусов для сферического треугольника со стороны a, b, c и

углами А, В, С имеют следующий вид

cos(c) = cos(a)*cos(b)+sin(a)*sin(b)*cosC

cosA = -cosB*cosC+sinB*sinC*cos(a)

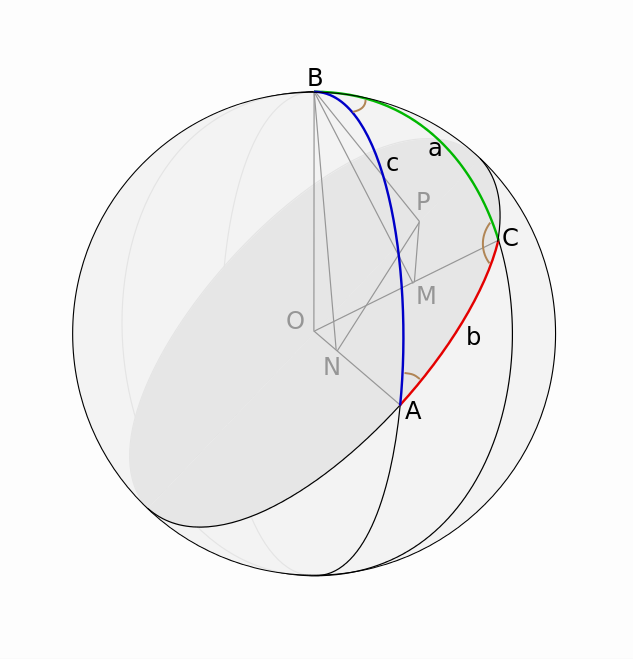
Доказательство проведём с помощью проекции. На рисунке показан сферический треугольник АВС на сфере радиуса R с центром в точке О. ВР- перпендикуляр к плоскости большого круга, проходящего через сторону b, ВМ- перпендикуляр к ОС, BN-перпендикуляр к ОА. По утверждению, обратному теореме о трёх перпендикулярах, РМ- перпендикуляр к ОС, PN-перпендикуляр к ОА. Заметим, что угол РМВ равен п-С, кроме того, ОМ=R cos и OM=R cos(a). Далее проецируем ломаную OMPN прямую, содержащую ON.



Pr ON= pr OM+ pr MP+ pr PN

PN перпендикуляр ОА- pr PN= O

Pr OM= OM cos(b)= R cos(a)*cos(b)

Pr MP= PM cos (п-(п/2-
Подставляем три последних выражения и указанное выше выражение ON= R cos в первое выражение и получаем:

cos(c)= cos(a)*cos(b)+ sin(a)*sin(b)*cosC

Теоремы косинусов для двух других сторон, т.е теорему для cos(a) и теорему для cos(b) , их также можно получить сразу из формулы для стороны при помощи круговой перестановки букв: a – b – c - a, A –B – C - A
Вывод:

Тригонометрия нашла отражение в нашей жизни и сфере, в которых она играет важную роль, будут расширяться.

---