Файл: "Методы решения систем линейных алгебраических уравнений. Метод прогонки. Итерационные методы решения систем линейных алгебраических уравнений. Метод Якоби. Метод верхней релаксации. Метод Зейделя".docx

Семестровая работа по численным методам на тему:

“Методы решения систем линейных алгебраических уравнений. Метод прогонки. Итерационные методы решения систем линейных алгебраических уравнений. Метод Якоби. Метод верхней релаксации. Метод Зейделя”

Оглавление

Оглавление…………………………………………………………………..2

Постановка задачи

Дана система линейных уравнений следующего вида:













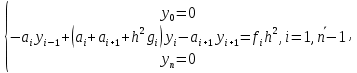
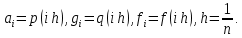
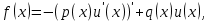
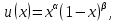
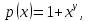
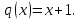
Необходимо найти значения 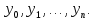Для проверки точности решений системы линейных уравнений используется следующее отношение:

.

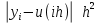Решение задачи

Дано: 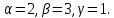Найдем значения функций: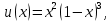







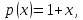
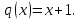
Полученное значение :



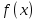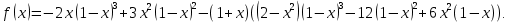
Для решения системы используем метод прогонки.

Рассмотрим метод прогонки для решения системы линейных уравнений вида:



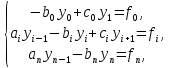
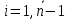
Вычисляем 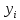по формуле прогонки: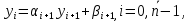





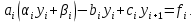
Таким образом, получаем равенство:



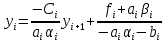
Сравнивая

---

формулы прогонки и последнее равенство, получим рекуррентные формулы для вычисления коэффициентов прогонки:



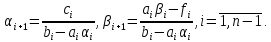
Если из первого уравнения системы выразим 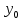, то можно найт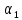и и :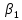



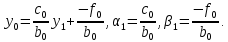
Зная 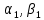, найдем все остальные 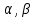. Вычисление всех коэффициентов прогонки называется прямым методом прогонки.

Необходимо вычислить все по формуле 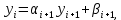для 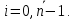Для этого понадобится значение 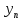, которое мы получим исключением 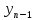из последнего уравнения системы: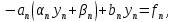



.

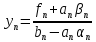Данные вычисления называются обратным ходом метода прогонки. Данный метод применим только для систем уравнений с трёхдиагональной матрицей.

Достаточным условием корректности и устойчивости метода прогонки является условие преобладания диагональных элементов в матрице, то есть должны быть выполнены следующие условия:







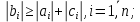
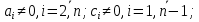
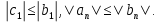
Проверим выполнение этих условий для решаемой системы:

---

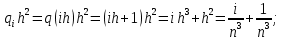
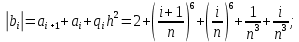
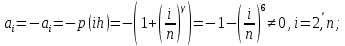
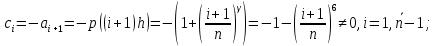
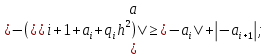
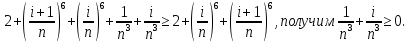
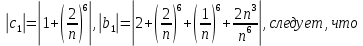
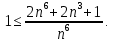
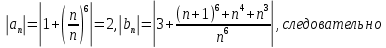
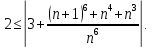
Таким образом, условие устойчивости метода прогонки выполнено.

Результаты вычислений при :



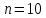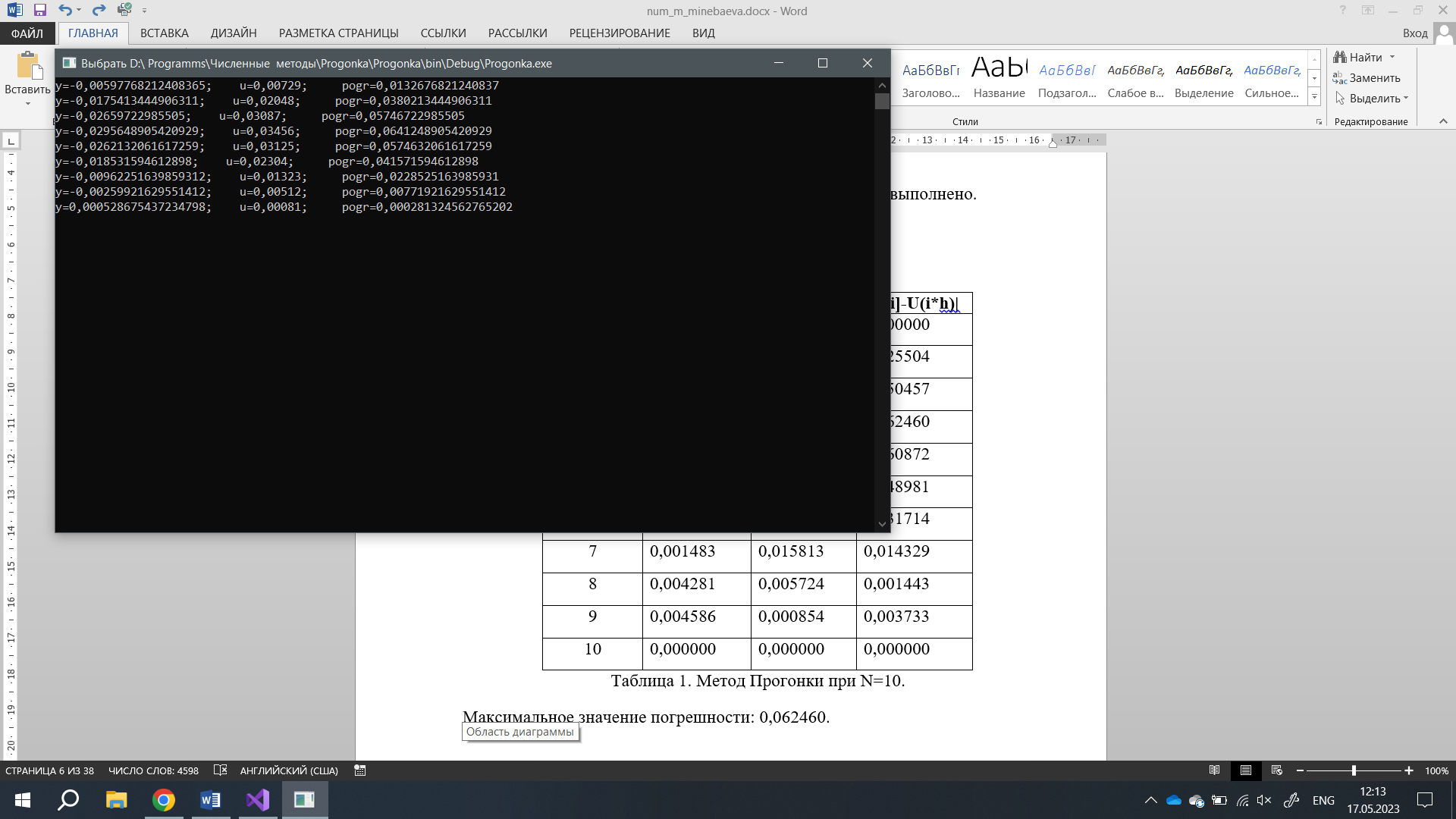
Максимальное значение погрешности: 0,0641248905420929.

Результаты вычислений при :



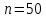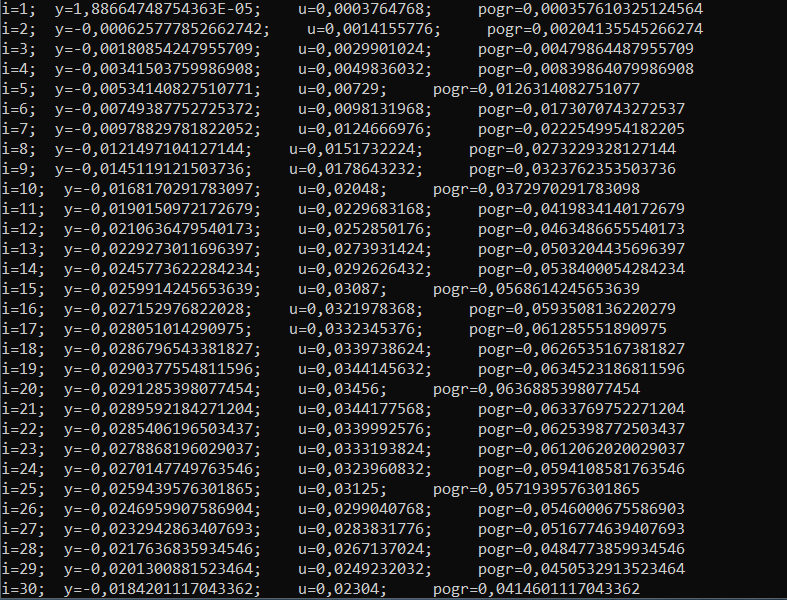
Максимальное значение погрешности: 0,0636885398077454.

Результаты вычислений при :



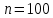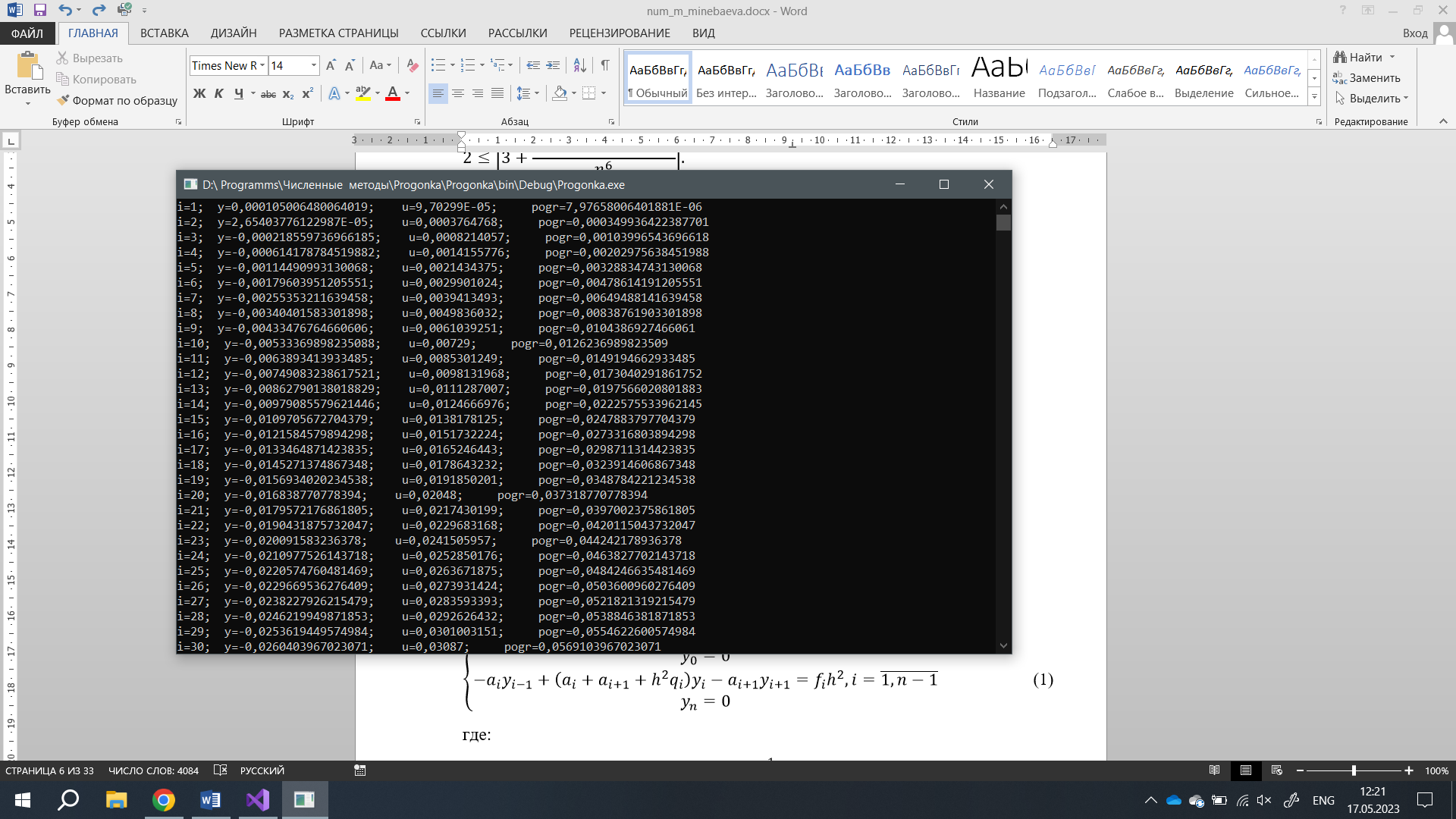
Максимальное значение погрешности: 0,0637485714033385.

Метод Якоби.

Общий вид метода Якоби:



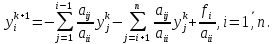
Вектор 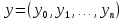вычисляем путем последовательного вычисления каждой следующей итерации на основе предыдущей.

Для системы (1) метод Якоби запишем следующим образом:



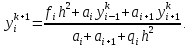
Будем искать каждую следующую итерацию, пока не выполнится условие:



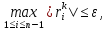
где

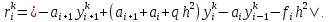
В качестве начального приближения берём нулевой вектор:

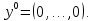
Теорема сходимости: если в системе выполняется диагональное преобладание, то метод Якоби сходится от любого начального приближения.

Матрица А называется матрицей с диагональным преобладанием, если:



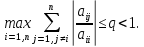
Результаты вычислений для системы (1) при :

---

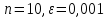Количество итераций: 26

Максимальная погрешность: 0,0587307781342732

Результаты вычислений для системы (1) при :

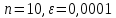Количество итераций: 68

Максимальная погрешность: 0,0635788881625071

Результаты вычислений для системы (1) при :

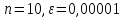Количество итераций: 75

Максимальная погрешность: 0,039309310580449904

Дальше менять 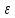нет смысла, поскольку погрешность меняется не сильно.

Результаты вычислений для системы (1) при :

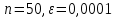Количество итераций: 222

Максимальная погрешность: 0,049460828748177

Результаты вычислений для системы (1) при :

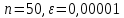Количество итераций: 1243

Максимальная погрешность: 0,0621848973450342

Результаты вычислений для системы (1) при :

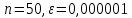Количество итераций: 2314

Максимальная погрешность: 0,0635383497725728

Дальше менять 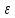нет смысла, поскольку погрешность меняется не сильно.

Результаты вычислений для системы (1) при :

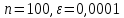Количество итераций: 14

Максимальная погрешность: 0,0350321873013994

Результаты вычислений для системы (1) при :

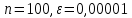Количество итераций: 2380

Максимальная погрешность: 0,0576423968520161

Результаты вычислений для системы (1) при :

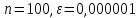Количество итераций: 6670

Максимальная погрешность: 0,0631435175839205

Дальше менять 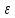нет смысла, поскольку погрешность меняется не сильно.

Метод Зейделя.

Метод Зейделя представляет собой некоторую модификацию метода Якоби. Основная его идея заключается в том, что при вычислении (k + 1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k + 1)-е приближения неизвестных x₁, x₂, …, x_{i - 1}.

Общая формула:

---

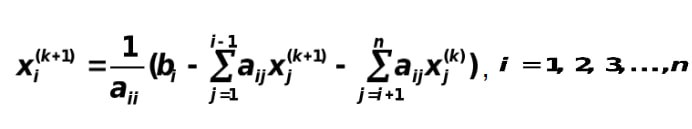
Пусть получена эквивалентная система (4.5). Выберем произвольно начальные приближения корней  . Далее, предполагая, что k-ые приближения  корней известны, согласно Зейделю будем строить (k + 1)-е приближения корней по формулам:

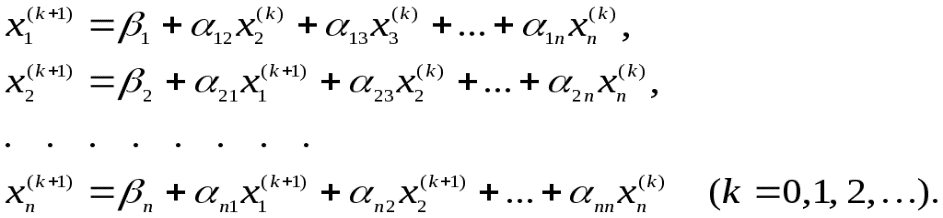 (4.5)

Заметим, что указанные выше условия сходимости для простой итерации остается верной для итерации по методу Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации, но приводит к более громоздким вычислениям.

Результаты вычислений при :

Количество итераций: 12

Максимальная погрешность: 0,058319817675039

Результаты вычислений при :

Количество итераций: 33

Максимальная погрешность: 0,0635402535885495

Дальше менять нет смысла, поскольку погрешность меняется не сильно.

Результаты вычислений при :

Количество итераций: 112

Максимальная погрешность: 0,0495658385769455

Результаты вычислений при :

Количество итераций: 615

Максимальная погрешность: 0,0621556241400929

Дальше менять нет смысла, поскольку погрешность меняется не сильно.

Результаты вычислений при :

Количество итераций: 7

Максимальная погрешность: 0,03503260655369

Результаты вычислений при :

Количество итераций: 1177

Максимальная погрешность: 0,0575808416386456

Результаты вычислений при :

Количество итераций: 999

Максимальная погрешность: 0,03858973176411326

Дальше менять нет смысла, поскольку погрешность меняется не сильно.

Метод верхней релаксации.

---