Файл: "Методы решения систем линейных алгебраических уравнений. Метод прогонки. Итерационные методы решения систем линейных алгебраических уравнений. Метод Якоби. Метод верхней релаксации. Метод Зейделя".docx

Общий вид метода верхней релаксации:



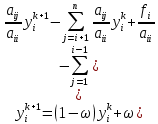
где .

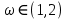Вектор вычисляем путем последовательного вычисления каждой следующей итерации на основе предыдущей.

Для системы (1) метод верхней релаксации выглядит следующим образом:



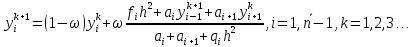
Будем находить каждую следующую итерацию до тех пор, пока не выполнится условие:



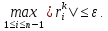
Возьмем в качестве начального приближения нулевой вектор: Необходимо найти такой параметр 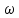, при котором количество итераций будет наименьшим.

Пусть

Наименьшее число итераций равно 6 при

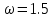
Максимальная погрешность для данной 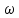: 0,062853823015049

Пусть

Наименьшее число итераций равно 10 при

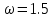
Максимальная погрешность для данной 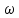: 0,0639706161866553

Пусть

Наименьшее число итераций равно 24 при

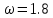
Максимальная погрешность для данной 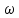: 0,0560119004070355

Пусть

Наименьшее число итераций равно 50 при

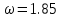
Максимальная погрешность для данной 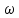: 0,0629145057540772

Пусть

Наименьшее число итераций равно 3 при

---

Максимальная погрешность для данной : 0,0351522803619569

Пусть

Наименьшее число итераций равно 87 при

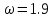
Максимальная погрешность для данной : 0,0608771959171397

Вывод.

Метод верхней релаксации работает эффективнее метода Зейделя. Метод Зейделя работает эффективнее метода Якоби.

Листинг программы

Метод прогонки

using System;

namespace Progonka

{

class Program

{

static void Main(string[] args)

{

int n = 50;

double h = 1.0 / n;

double a, a1, a2, b, c;

double g, f, u, maxpogr=0;

double[] P = new double[n];

double[] Q = new double[n];

double[] y = new double[n];
a1 = 1 + h;

a2 = 1 + 2 * h;

g = h + 1;

b = -(a1 + a2 + h * h * g);

c = -a2;

f = ((2 * h * Math.Pow((1 - h), 3) - 3 * h * h * (1 - h) * (1 - h) + (1 + h) * (2 * Math.Pow((1 - h), 3) - 12*h * (1 - h) * (1 - h) + 6 * h * h * (1 - h))) + (1 + h) * h * h * Math.Pow((1 - h), 3))*h*h;

P[2] = c / b;

Q[2] = -f / b;
for (int i = 2; i < n-1; i++)

{

a1 = (1 + i * h);

a2 = (1 + (i + 1) * h);

a = -a1;

g = i * h + 1;

b = -(a1 + a2 + h * h * g);

c = -a2;

f = ((2 * i*h * Math.Pow((1 - i*h), 3) - 3 * i*h * i*h * (1 - i*h) * (1 - i*h) + (1 + i*h) * (2 * Math.Pow((1 - i*h), 3) - 12 *i*h* (1 - i*h) * (1 - i*h) + 6 * i*h * i*h * (1 - i*h))) + (1 + i*h) * i*h * i*h * Math.Pow((1 - i*h), 3))*h*h;

P[i + 1] = c / (b - a * P[i]);

Q[i + 1] = (a * Q[i] - f) / (b - a * P[i]);

}
a1 = (1 + (n - 1) * h);

a2 = (1 + n*h);

a = -a1;

g = (n-1) * h + 1;

b = -(a1 + a2 + h * h * g);

f = ((2 * (n-1) * h * Math.Pow((1 - (n-1) * h), 3) - 3 * (n-1) * h * (n-1) * h * (1 - (n-1) * h) * (1 - (n-1) * h) + (1 + (n-1) * h) * (2 * Math.Pow((1 - (n-1) * h), 3) - 12*(n-1)*h * (1 - (n-1) * h) * (1 - (n-1) * h) + 6 * (n-1) * h * (n-1) * h * (1 - (n-1) * h))) + (1 + (n-1) * h) * (n-1) * h * (n-1) * h * Math.Pow((1 - (n-1) * h), 3)) * h * h;

y[n - 1] = (a*Q[n-1]-f)/(b-a*P[n-1]);
for (int i=n-1; i>1; i--)

{

y[i - 1] = P[i] * y[i] + Q[i];

}
for (int i=1; i
{

u = (i * h * i * h * Math.Pow((1 - i * h), 3));

Console.WriteLine("i="+i+"; y=" + y[i] +"; u=" +u + "; pogr=" + Math.Abs(y[i] - u));

if (Math.Abs(y[i] - u) > maxpogr)

maxpogr = Math.Abs(y[i] - u);

}

Console.WriteLine(maxpogr);
Console.ReadKey();

}

}

}

Метод Якоби

using System;
namespace Yakobi

{

class Program

{

static void Main(string[] args)

{

int n = 100, k=0;

double h = 1.0 / n;

double a1, a2, a, b, c, max=1, u, maxpogr=0;

double[] x = new double[n];

double[] y = new double[n];

double[] f = new double[n];

double[] r = new double[n];

double[] g = new double[n];
for (int i=1; i
{

g[i] = i * h + 1;

f[i] = ((2 * i * h * Math.Pow((1 - i * h), 3) - 3 * i * h * i * h * (1 - i * h) * (1 - i * h) + (1 + i * h) * (2 * Math.Pow((1 - i * h), 3) - 12 * i * h * (1 - i * h) * (1 - i * h) + 6 * i * h * i * h * (1 - i * h))) + (1 + i * h) * i * h * i * h * Math.Pow((1 - i * h), 3)) * h * h;

y[i] = 0;

}
while (max > 0.000001)

{

max = 0;

for (int i = 1; i < n; i++)

{

x[i] = y[i];

}

a1 = 1 + h;

a2 = 1 + 2 * h;

---

b = a1 + a2 + h * h * g[1];

c = -a2;

y[1] = -c * x[2] / b + f[1] / b;
for (int i=2; i
{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

y[i] = -a * x[i - 1] / b - c * x[i + 1] / b + f[i] / b;

}
a1 = 1 + (n-1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n-1];

y[n - 1] = -a * x[n - 2] / b + f[n - 1] / b;
a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

r[1] = f[1] - b * y[1] - c * y[2];

for (int i=2; i
{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

r[i] = f[i] - a * y[i - 1] - b * y[i] - c * y[i + 1];

}

a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

r[n - 1] = f[n - 1] - a * y[n - 2] - b * y[n - 1];
for (int i = 1; i < n; i++)

{

if (Math.Abs(r[i]) > max)

max = Math.Abs(r[i]);

}

k++;

}

Console.WriteLine(k);
for (int i = 1; i < n; i++)

{

u = (i * h * i * h * Math.Pow((1 - i * h), 3));

Console.WriteLine("pogr=" + Math.Abs(y[i]-u));

if (Math.Abs(y[i] - u) > maxpogr)

maxpogr = Math.Abs(y[i] - u);

}

Console.WriteLine(maxpogr);

Console.ReadKey();

}

}

}

Метод Зейделя

using System;
namespace Zeidel

{

class Program

{

static void Main(string[] args)

{

int n = 100, k = 0;

double h = 1.0 / n;

double a1, a2, a, b, c, max = 1, u, maxpogr=0;

double[] x = new double[n];

double[] y = new double[n];

double[] f = new double[n];

double[] r = new double[n];

double[] g = new double[n];
for (int i = 1; i < n; i++)

{

g[i] = i * h + 1;

f[i] = ((2 * i * h * Math.Pow((1 - i * h), 3) - 3 * i * h * i * h * (1 - i * h) * (1 - i * h) + (1 + i * h) * (2 * Math.Pow((1 - i * h), 3) - 12 * i * h * (1 - i * h) * (1 - i * h) + 6 * i * h * i * h * (1 - i * h))) + (1 + i * h) * i * h * i * h * Math.Pow((1 - i * h), 3)) * h * h;

y[i] = 0;

}
while (max > 0.000001)

{

max = 0;

for (int i = 1; i < n; i++)

{

x[i] = y[i];

}

a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

y[1] = -c * x[2] / b + f[1] / b;
for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

y[i] = -a * y[i - 1] / b - c * x[i + 1] / b + f[i] / b;

}
a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

y[n - 1] = -a * y[n - 2] / b + f[n - 1] / b;
a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

r[1] = f[1] - b * y[1] - c * y[2];

for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

r[i] = f[i] - a * y[i - 1] - b * y[i] - c * y[i + 1];

}

a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

r[n - 1] = f[n - 1] - a * y[n - 2] - b * y[n - 1];
for (int i = 1; i < n; i++)

{

if (Math.Abs(r[i]) > max)

max = Math.Abs(r[i]);

}

k++;

}

Console.WriteLine(k);
for (int i = 1; i < n; i++)

{

u = (i * h * i * h * Math.Pow((1 - i * h), 3));

Console.WriteLine("pogr=" + Math.Abs(y[i] - u));

if (Math.Abs(y[i] - u) > maxpogr)

maxpogr = Math.Abs(y[i] - u);

}

Console.WriteLine(maxpogr);
Console.ReadKey();

}

}

}

Метод верхней релаксации

using System;
namespace Relax

{

class Program

{

static void Main(string[] args)

{

int n = 100, k = 0;

double h = 1.0 / n;

double a1, a2, a, b, c, max = 1, u, w, minw=1, mink=100000, e=0.00001, maxpogr=0;

double[] x = new double[n];

double[] y = new double[n];

double[] f = new double[n];

double[] r = new double[n];

---

double[] g = new double[n];
for (int i = 1; i < n; i++)

{

g[i] = i * h + 1;

f[i] = ((2 * i * h * Math.Pow((1 - i * h), 3) - 3 * i * h * i * h * (1 - i * h) * (1 - i * h) + (1 + i * h) * (2 * Math.Pow((1 - i * h), 3) - 12 * i * h * (1 - i * h) * (1 - i * h) + 6 * i * h * i * h * (1 - i * h))) + (1 + i * h) * i * h * i * h * Math.Pow((1 - i * h), 3)) * h * h;

}
for (w = 1; w <= 2; w += 0.05)

{

for (int i = 1; i < n; i++)

y[i] = 0;

k = 0;

max = 1;

while (max > e)

{

max = 0;

for (int i = 1; i < n; i++)

{

x[i] = y[i];

}

a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

y[1] = (1-w)*x[1]+w*( -c * x[2] / b + f[1] / b);
for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

y[i] = (1-w)*x[i]+w*(-a * y[i - 1] / b - c * x[i + 1] / b + f[i] / b);

}
a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

y[n - 1] = (1-w)*x[n-1]+w*(-a * y[n - 2] / b + f[n - 1] / b);
a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

r[1] = f[1] - b * y[1] - c * y[2];

for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

r[i] = f[i] - a * y[i - 1] - b * y[i] - c * y[i + 1];

}

a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

r[n - 1] = f[n - 1] - a * y[n - 2] - b * y[n - 1];
for (int i = 1; i < n; i++)

{

if (Math.Abs(r[i]) > max)

max = Math.Abs(r[i]);

}

k++;

}

Console.WriteLine("w="+w+"; k="+k);

if (k < mink)

{

mink = k;

minw = w;

}

}
for (int i = 1; i < n; i++)

y[i] = 0;

k = 0;

max = 1;

while (max > e)

{

max = 0;

for (int i = 1; i < n; i++)

{

x[i] = y[i];

}

a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

y[1] = (1 - minw) * x[1] + minw * (-c * x[2] / b + f[1] / b);
for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

y[i] = (1 - minw) * x[i] + minw * (-a * y[i - 1] / b - c * x[i + 1] / b + f[i] / b);

}
a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

y[n - 1] = (1 - minw) * x[n - 1] + minw*(-a * y[n - 2] / b + f[n - 1] / b);
a1 = 1 + h;

a2 = 1 + 2 * h;

b = a1 + a2 + h * h * g[1];

c = -a2;

r[1] = f[1] - b * y[1] - c * y[2];

for (int i = 2; i < n - 1; i++)

{

a1 = 1 + i * h;

a2 = 1 + (i + 1) * h;

a = -a1;

b = a1 + a2 + h * h * g[i];

c = -a2;

r[i] = f[i] - a * y[i - 1] - b * y[i] - c * y[i + 1];

}

a1 = 1 + (n - 1) * h;

a2 = 1 + n * h;

a = -a1;

b = a1 + a2 + h * h * g[n - 1];

r[n - 1] = f[n - 1] - a * y[n - 2] - b * y[n - 1];
for (int i = 1; i < n; i++)

{

if (Math.Abs(r[i]) > max)

max = Math.Abs(r[i]);

}

k++;

}

Console.WriteLine("minw=" + minw + "; k=" + k);
for (int i = 1; i < n; i++)

{

u = (i * h * i * h * Math.Pow((1 - i * h), 3));

Console.WriteLine("pogr=" + Math.Abs(y[i] - u));

if (Math.Abs(y[i] - u) > maxpogr)

maxpogr = Math.Abs(y[i] - u);

}

Console.WriteLine(maxpogr);
Console.ReadKey();

}

}

}

Список литературы

1. Мацокин А. М., Сорокин С. Б. «Численные методы.».

2. Калинтин Н. Н. «Численные методы».

3. Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. «Численные методы».

4. Колдаев В.Д. Численные методы и программирование. - Москва: ИНФРА-М, 2009

---