Добавлен: 22.11.2023
Просмотров: 184
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
, то она определяется совместным заданием двух уравнением:
A1x + B1y + C1z + D1 = 0,
A2x + B2y + C2z + D2 = 0.
Поставим задачу: всегда ли два уравнения первой степени совместно определяют некоторую прямую? Очевидно, это будет только в том случае, когда соответствующие им плоскости не параллельны и не совпадают друг с другом, т.е. когда нормальные векторы этих плоскостей N1 = {A1, B1, C1}и N2 = {A2, B2, C2}не коллинеарны. Эти два уравнения совместно определяют прямую только в том случае, когда коэффициенты A1, B1, C1 одного из них не пропорциональны коэффициентам A2, B2, C2 другого.
Пусть имеем два уравнения с тремя переменными
f1(x, y, z) = 0 и f2(x, y, z) = 0.
Каждое из них определяет некоторую поверхность. Множество точек, общих обеим поверхностям, есть некоторая линия.
Пример. Уравнения x2 + y2 = R2 и z = a, радиуса R с центром на оси Ozв точке (0; 0; a). Заметим, что эту же линию можно задать параметрически тремя уравнениямиx = Rcos φ, y = Rsin φ, z = a.
В общем случае параметрические уравнения линии имеют вид:
x = x(t), y = y(t), z = z(t).
Рассмотрим произвольную прямую. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором данной прямой. Указанные векторы называются направляющими именно потому, что любой из них, будучи задан, определяет направление прямой.
Направляющий вектор прямой будем обозначать буквой l, его координаты – m, n, p:
l = {m;n; p}.
Пусть дана точкаM0 (x0; y0; z0)и ненулевой векторs (m; p;
q).Требуется составить уравнение прямой l, проходящей через точку M0и параллельной вектору s (этот вектор называют направляющим вектором прямой). Для этого заметим, что точка M (x; y; z) лежит на указанной прямой тогда и только тогда, когда векторы M0M (x - x0; y - y0; z - z0)и s (m; p; q)коллинеарны, т.е. тогда, когда координаты этих векторов пропорциональны:
x–x0 = y – y0= z – z0.
mpq
Данные уравнения называются каноническими уравнениями прямой l.
Пример. Написать каноническое уравнение прямой, проходящей через точку M0( -2; -3; -1) и имеющей направляющий вектор s (3; 2; 4). Согласно равенствам имеем:
x + 2 = y + 3 = z + 1.
324
Пусть прямая l задана каноническими уравнениями. Причем за параметр tкаждое из отношений. Так как один из знаменателей отличен от нуля, а соответствующий числитель может принимать какие угодно значения, то областью изменения параметра tявляется вся числовая ось - ∞ <t< + ∞. Получим:
x – x0 = mt, y – y0 = pt, z – z0 = qt,
или
x = x0 + mt, y – y0 + pt, z = z0 + qt.
Данные уравнения и есть искомые параметрические уравнения прямой.
Пример. Составить параметрическое уравнение прямой, проходящей через точку M0(2; -3; -7) и имеющей направляющий вектор s (4; -6; 5). Согласно равенствам имеем:
x = 2 + 4t, y = -3 – 6t, z = -7 + 5t.
Следующие две задачи имеют большое значение.
Задача 1. Даны точка M0(x0, y0) и число m. Требуется провести через M0прямую, имеющую m своим угловым коэффициентом.
Решение. Будем искать уравнение нужной нам прямой в форме
y = mx + b.
Это даст для b значение
b = y0 – mx
0.
Подставляя это значение в уравнение, получаем уравнение искомой прямой
y = mx + y0 – mx0.
Обычно его записывают в виде
y – y0 = m(x – x0).
Пример.Провести через M0(5, 2) прямую, перпендикулярную прямой
3x – 2y + 6 = 0.
Решение. Угловой коэффициент прямой равен 3/2. Поэтому (на основании условия перпендикулярности) угловой коэффициент m искомой прямой будет m = - 2/3. Значит, требуемое уравнение такого:
y – 2 = - 2/3 (x – 5)
или то же самое,
2x + 3y – 16 = 0.
Задача 2.Провести прямую через две заданные точки M1 (x1; y1) и M2 (x2; y2).
Решение. Обозначим через m(неизвестный) угловой коэффициент искомой прямой. Так как эта прямая проведена через точку M1 (x1; y1), то ее уравнение должно иметь вид
y – y1 = m(x – x1).
Для нахождения m используем то, что наша прямая проходит и через M2 (x2; y2) и, стало быть, числа x2y2должны удовлетворять уравнению, т.е.
y2 – y1 = m (x2 – x1),
откуда
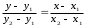 .
.
Задача решена.
Если y1 = y2, то уравнение искомой прямой имеет вид y = y1. В этом случае прямая параллельна оси Оx. Если x1 = x2, то прямая, проходящая через точки M1и M2, параллельна оси Oy, и ее уравнение имеет вид x = x1.
Пример.Составить уравнение прямой, проходящей через точки M1 (3; 1) иM2 (5; 4). Подставляя координаты точек M1 и M2 в уравнение, получаем искомое уравнение прямой:
x – 3 = y - 1
2 3 ,
или
3x – 2y – 7 = 0.
При написании данной курсовой работы стремилось раскрыться содержание основных понятий аналитической геометрии по теме «Прямая на плоскости и в пространстве», изучились основные уравнения прямой, привелись примеры. Изложение материала по возможности полно и доступно
, так как преследовалась цель сообщить основные сведения по данной теме.
Опыт показал, что для многих начинающих значительную трудность представляет решение типовых примеров и задач, поясняющих теоретический материал. Однако прежде, чем начать рассматривать пример или задачу, надо сначала изучить нужный раздел и добиться полной ясности в понимании соответствующих понятий и теорем. Поэтому в данную работу включены типовые задачи и даются методы их решения, чтобы материал лучше закрепился.
Изучение математики и её методов в экономике, составляющих основу современной экономической математики, позволит будущему специалисту приобрести необходимые базовые навыки, расширить кругозор, повысить уровень мышления и общую культуру. Все это понадобится ему для ориентации в профессиональной деятельности и успешной работе.
1 Баврин И.И, Матросов В.Л. Высшая математика. «Гуманитарный издательский центр ВЛАДОС», М., 2002 г, - 400 с.
2 Данко П.Е., Кожевникова Т.Я.,Попов А.Г. Высшая математика в упражнениях и задачах.В 2-х ч. 5-е изд., изд. «Высшая школа» М.,1997 г, -304с.
3 Натансон И.П. Краткий курс высшей математики. 6-е изд., стер. – СПб.: Издательство«Лань», 2003 г, - 736 с.: ил.
4 Шипачёв В.С. Основы высшей математики: учеб. Пособие для вузов/ под ред. Акад. А.Н. Тихонова. – 3-е изд., М.: Высш. школа, 1998. – 479 с.: ил.
5 Большой энциклопедический словарь под ред. Ю.В. Прохорова. Изд. «Большая Российская Энциклопедия». М., 2000. – 846 с
1 Большой энциклопедический словарь под ред. Ю.В. Прохорова. Изд. «Большая Российская Энциклопедия». М., 2000. – 846 с.
A1x + B1y + C1z + D1 = 0,
A2x + B2y + C2z + D2 = 0.
Поставим задачу: всегда ли два уравнения первой степени совместно определяют некоторую прямую? Очевидно, это будет только в том случае, когда соответствующие им плоскости не параллельны и не совпадают друг с другом, т.е. когда нормальные векторы этих плоскостей N1 = {A1, B1, C1}и N2 = {A2, B2, C2}не коллинеарны. Эти два уравнения совместно определяют прямую только в том случае, когда коэффициенты A1, B1, C1 одного из них не пропорциональны коэффициентам A2, B2, C2 другого.
2.2 Геометрическое истолкование двух уравнений между координатами в пространстве
Пусть имеем два уравнения с тремя переменными
f1(x, y, z) = 0 и f2(x, y, z) = 0.
Каждое из них определяет некоторую поверхность. Множество точек, общих обеим поверхностям, есть некоторая линия.
Пример. Уравнения x2 + y2 = R2 и z = a, радиуса R с центром на оси Ozв точке (0; 0; a). Заметим, что эту же линию можно задать параметрически тремя уравнениямиx = Rcos φ, y = Rsin φ, z = a.
В общем случае параметрические уравнения линии имеют вид:
x = x(t), y = y(t), z = z(t).
2.3 Направляющий вектор прямой
Рассмотрим произвольную прямую. Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором данной прямой. Указанные векторы называются направляющими именно потому, что любой из них, будучи задан, определяет направление прямой.
Направляющий вектор прямой будем обозначать буквой l, его координаты – m, n, p:
l = {m;n; p}.
2.4Каноническое уравнение прямой
Пусть дана точкаM0 (x0; y0; z0)и ненулевой векторs (m; p;
q).Требуется составить уравнение прямой l, проходящей через точку M0и параллельной вектору s (этот вектор называют направляющим вектором прямой). Для этого заметим, что точка M (x; y; z) лежит на указанной прямой тогда и только тогда, когда векторы M0M (x - x0; y - y0; z - z0)и s (m; p; q)коллинеарны, т.е. тогда, когда координаты этих векторов пропорциональны:
x–x0 = y – y0= z – z0.
mpq
Данные уравнения называются каноническими уравнениями прямой l.
Пример. Написать каноническое уравнение прямой, проходящей через точку M0( -2; -3; -1) и имеющей направляющий вектор s (3; 2; 4). Согласно равенствам имеем:
x + 2 = y + 3 = z + 1.
324
2.5 Параметрическое уравнения прямой в пространстве
Пусть прямая l задана каноническими уравнениями. Причем за параметр tкаждое из отношений. Так как один из знаменателей отличен от нуля, а соответствующий числитель может принимать какие угодно значения, то областью изменения параметра tявляется вся числовая ось - ∞ <t< + ∞. Получим:
x – x0 = mt, y – y0 = pt, z – z0 = qt,
или
x = x0 + mt, y – y0 + pt, z = z0 + qt.
Данные уравнения и есть искомые параметрические уравнения прямой.
Пример. Составить параметрическое уравнение прямой, проходящей через точку M0(2; -3; -7) и имеющей направляющий вектор s (4; -6; 5). Согласно равенствам имеем:
x = 2 + 4t, y = -3 – 6t, z = -7 + 5t.
2.6 Уравнение прямой по одной или двум точкам
Следующие две задачи имеют большое значение.
Задача 1. Даны точка M0(x0, y0) и число m. Требуется провести через M0прямую, имеющую m своим угловым коэффициентом.
Решение. Будем искать уравнение нужной нам прямой в форме
y = mx + b.
Это даст для b значение
b = y0 – mx
0.
Подставляя это значение в уравнение, получаем уравнение искомой прямой
y = mx + y0 – mx0.
Обычно его записывают в виде
y – y0 = m(x – x0).
Пример.Провести через M0(5, 2) прямую, перпендикулярную прямой
3x – 2y + 6 = 0.
Решение. Угловой коэффициент прямой равен 3/2. Поэтому (на основании условия перпендикулярности) угловой коэффициент m искомой прямой будет m = - 2/3. Значит, требуемое уравнение такого:
y – 2 = - 2/3 (x – 5)
или то же самое,
2x + 3y – 16 = 0.
Задача 2.Провести прямую через две заданные точки M1 (x1; y1) и M2 (x2; y2).
Решение. Обозначим через m(неизвестный) угловой коэффициент искомой прямой. Так как эта прямая проведена через точку M1 (x1; y1), то ее уравнение должно иметь вид
y – y1 = m(x – x1).
Для нахождения m используем то, что наша прямая проходит и через M2 (x2; y2) и, стало быть, числа x2y2должны удовлетворять уравнению, т.е.
y2 – y1 = m (x2 – x1),
откуда
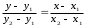 .
.Задача решена.
Если y1 = y2, то уравнение искомой прямой имеет вид y = y1. В этом случае прямая параллельна оси Оx. Если x1 = x2, то прямая, проходящая через точки M1и M2, параллельна оси Oy, и ее уравнение имеет вид x = x1.
Пример.Составить уравнение прямой, проходящей через точки M1 (3; 1) иM2 (5; 4). Подставляя координаты точек M1 и M2 в уравнение, получаем искомое уравнение прямой:
x – 3 = y - 1
2 3 ,
или
3x – 2y – 7 = 0.
Заключение
При написании данной курсовой работы стремилось раскрыться содержание основных понятий аналитической геометрии по теме «Прямая на плоскости и в пространстве», изучились основные уравнения прямой, привелись примеры. Изложение материала по возможности полно и доступно
, так как преследовалась цель сообщить основные сведения по данной теме.
Опыт показал, что для многих начинающих значительную трудность представляет решение типовых примеров и задач, поясняющих теоретический материал. Однако прежде, чем начать рассматривать пример или задачу, надо сначала изучить нужный раздел и добиться полной ясности в понимании соответствующих понятий и теорем. Поэтому в данную работу включены типовые задачи и даются методы их решения, чтобы материал лучше закрепился.
Изучение математики и её методов в экономике, составляющих основу современной экономической математики, позволит будущему специалисту приобрести необходимые базовые навыки, расширить кругозор, повысить уровень мышления и общую культуру. Все это понадобится ему для ориентации в профессиональной деятельности и успешной работе.
Список использованных источников
1 Баврин И.И, Матросов В.Л. Высшая математика. «Гуманитарный издательский центр ВЛАДОС», М., 2002 г, - 400 с.
2 Данко П.Е., Кожевникова Т.Я.,Попов А.Г. Высшая математика в упражнениях и задачах.В 2-х ч. 5-е изд., изд. «Высшая школа» М.,1997 г, -304с.
3 Натансон И.П. Краткий курс высшей математики. 6-е изд., стер. – СПб.: Издательство«Лань», 2003 г, - 736 с.: ил.
4 Шипачёв В.С. Основы высшей математики: учеб. Пособие для вузов/ под ред. Акад. А.Н. Тихонова. – 3-е изд., М.: Высш. школа, 1998. – 479 с.: ил.
5 Большой энциклопедический словарь под ред. Ю.В. Прохорова. Изд. «Большая Российская Энциклопедия». М., 2000. – 846 с
1 Большой энциклопедический словарь под ред. Ю.В. Прохорова. Изд. «Большая Российская Энциклопедия». М., 2000. – 846 с.