ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 23.11.2023
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Томский Государственный Университет
Систем управления и радиоэлектроники
(ТУСУР)
Контрольная работа № 4 по высшей математике.
Вариант №3.
Задание №1.
-
Найти производные от данных функций:
а).
Решение:
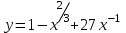
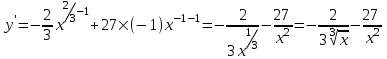
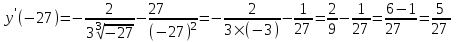
б).
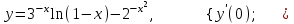
Решение:
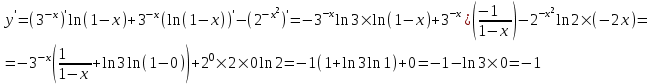
в).
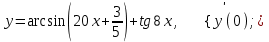
Решение:
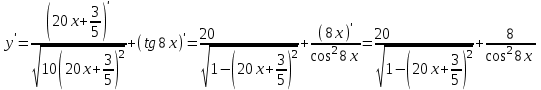
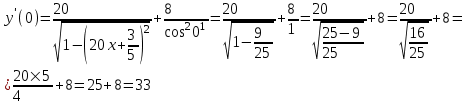
Задание №2.
Дана функция
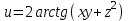
Найти: а). координаты вектора
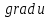 в точке А(-1,3,2);
в точке А(-1,3,2);Решение:
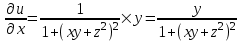 ;
;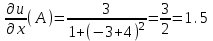
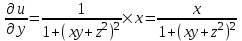 ;
;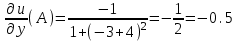
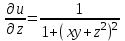 ;
;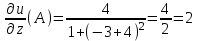
Координаты вектора
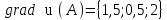
б).
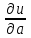 в точке A в направлении вектора
в точке A в направлении вектора 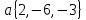 .
.Решение:
Найдем орт вектора а.
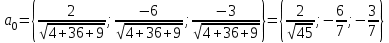
По формуле
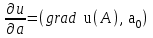 найдем
найдем  (А).
(А).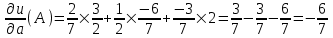
Задание №3.
Дана функция
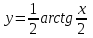 Найти
Найти 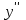 . Вычислить
. Вычислить 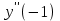 .
.Решение:
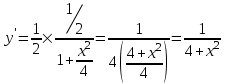
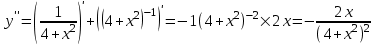
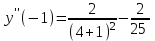
Задание №4.
Доказать, что функции
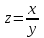 удовлетворяют уравнению
удовлетворяют уравнению 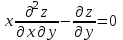
Решение:
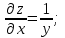
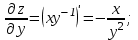
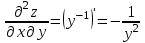
Видим, что

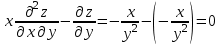 , что и требовалось доказать.
, что и требовалось доказать.Задание №5.
Найти
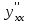 , если
, если 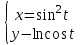 . Вычислить
. Вычислить 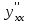 , если
, если 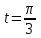 .
.Решение:
Найдем
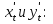

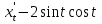
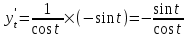 , следовательно,
, следовательно, 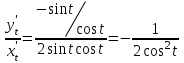 , поэтому,
, поэтому,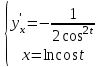
Так как
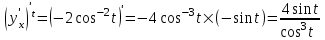 ;
;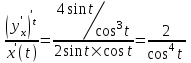 , то
, то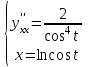
При
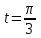 вторая производная
вторая производная 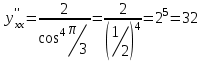
Задание №6.
Функция
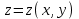 задана неявно уравнением
задана неявно уравнением 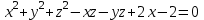
.
Вычислить:
а).
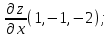 б).
б). 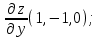
Решение:
Применим формулу
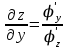 к функции
к функции 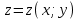 , заданной неявно уравнением
, заданной неявно уравнением 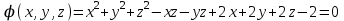
а).
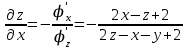 б).
б). 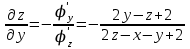
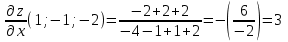
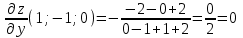
Задание №7
На графике функции
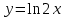 взята точка А. Касательная к графику в точке А наклонена к оси OX под углом, тангенс которого равен
взята точка А. Касательная к графику в точке А наклонена к оси OX под углом, тангенс которого равен 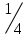 . Найти абсциссу точки A.
. Найти абсциссу точки A. Решение:
Найдем значение x точки A. Тангенс угла равен значению производной данной функции при данном значении x.
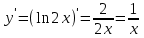
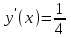
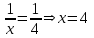 , то есть
, то есть 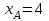 .
.Задание №8
Найти
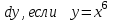 , вычислить значение
, вычислить значение 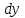 , если
, если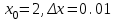 .
.Решение:
Найдем
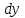 от функции
от функции 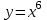 .
.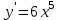 , найдем
, найдем 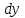 при
при 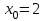 , а
, а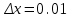 .
.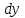 - это
- это 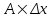 , где
, где 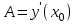 , а
, а 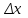 - называют приращением аргумента, следовательно:
- называют приращением аргумента, следовательно: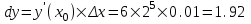
Задание №9
Дана функция
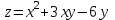 и точки
и точки 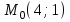 и
и 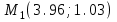 . Вычислить
. Вычислить 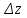 и
и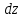 при переходе точки
при переходе точки 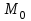 в точку
в точку 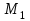 (ответы округлить до сотых).
(ответы округлить до сотых).Решение:
Находим
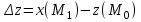
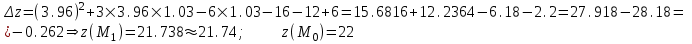 По формуле находим :
По формуле находим :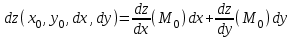
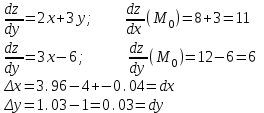
Найдем:
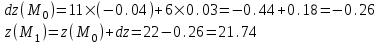
Задание №10
Дана функция
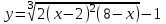 . Найти уу наибольшее и наименьшее значение на отрезке
. Найти уу наибольшее и наименьшее значение на отрезке 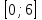 .
.Решение:
Найдем
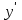 :
: 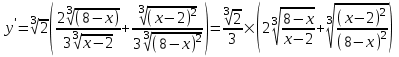
Критические точки:
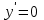
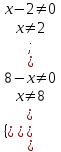
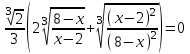
Разделим обе части уравнения на
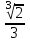 :
: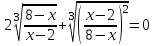
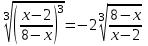
Домножим обе части уравнения на
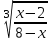
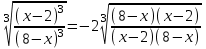
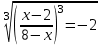
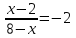
Домножим на
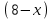 :
: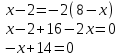
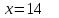 (критическая точка).
(критическая точка).При
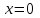 производной не существует,
производной не существует,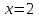 и
и 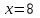 -точки разрыва.
-точки разрыва.Вычислим значение функции во всех найденных точках:
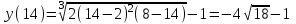 (не принадлежит отрезку)
(не принадлежит отрезку)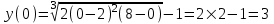
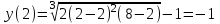
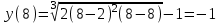 (не принадлежит отрезку)
(не принадлежит отрезку)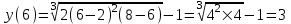
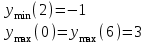
Задание №12
Провести полное исследование функции
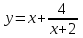 и начертить ее график.
и начертить ее график.Решение:
Найдем область определения функции
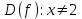
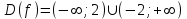 ;
;Найдем область значений
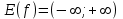 ;
;Выявить критические точки:
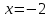 - точка разрыва второгорода.
- точка разрыва второгорода.Прямая
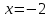 двустороняя вертикальная асимптота.
двустороняя вертикальная асимптота.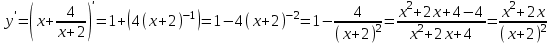
Находим наклонные асимптоты
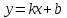
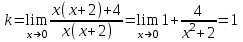

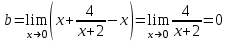 , следовательно, прямая
, следовательно, прямая 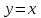 -наклонная двустороняя асимптота.
-наклонная двустороняя асимптота. , если
, если 
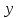 - не существует.
- не существует.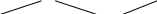


+ - +
-2 0
min
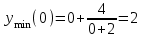
Исследуем функцию и окрестности точки
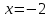 при
при 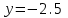
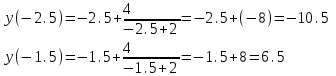
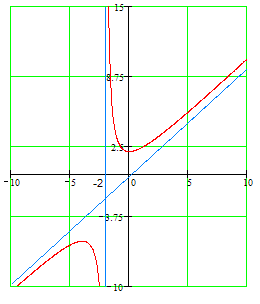
Так как знаменатель положителен всюду в