Файл: Решение прямой задачи методом неполной взаимозаменяемости (расчет вероятностным методом) 7.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 02.12.2023
Просмотров: 70
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
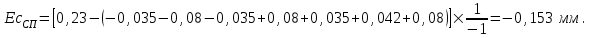
в) Определяем предельное отклонение специального звена:
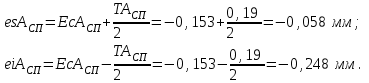
Таким образом, АСП.РАСЧ. =
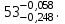
Ближайшим стандартным полем допуска является e10, предельные отклонения которого для АСП = 53 мм составляют
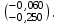
Проверим возможность принятия такого стандартного поля допуска для специального звена:
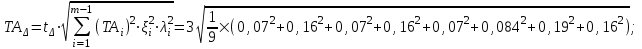
ТА = 0,368 мм.
 - 0,035 - 0,08 - 0,035 + 0,08 + 0,035 + 0,042 + 0,155 + 0,08;
- 0,035 - 0,08 - 0,035 + 0,08 + 0,035 + 0,042 + 0,155 + 0,08;ЕсА = + 0,242 мм.
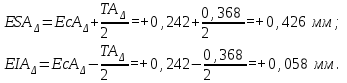
Таким образом
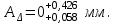
Анализируя полученный результат, делаем вывод о возможности принятия стандартного поля допуска АСП = 53e11
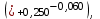 при котором, полностью удовлетворяются требования к замыкающему звену
при котором, полностью удовлетворяются требования к замыкающему звену 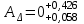 .
.3.6. Вывод: требуемая точность исходного звена при расчетах методом неполной взаимозаменяемости достигается при следующих размерах составляющих звеньев:
| А1 = 17+0,07 | А5 = 11-0,07 |
| А2 = 170-0,16 | А6 = 28-0,084 |
| А3 = 17+0,07 | А7 = 53e11 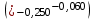 |
| А4 = 22-0,16 (задан) | А8 = 22-0,16 (задан) |
Вместе с тем, метод неполной взаимозаменяемости не удовлетворяет требованиям средней экономической точности.
4. Решение прямой задачи методом регулирования
Назначаем расширенные допуски на все звенья кроме компенсационного, по 11 квалитету (среднеэкономическая точность).
| ТА1 = 0,11 | ТА5 = 0,11 |
| ТА2 = 0,25 | ТА6 = 0,13 |
| ТА3 = 0,11 | ТА7 = 0,19 |
| ТА4 = 0,16 (задан) | ТА8 = 0,16 (задан) |
Определяем допуск замыкающего звена при принятых допусках составляющих звеньев:
ТА = 0,11 + 0,25 + 0,11 + 0,16 + 0,11 + 0,13 + 0,19 + 0,16 = 1,22 мм.
Назначаем предельные отклонения на все размеры (кроме одного – А7), как на основные валы и отверстия, соответственно по h11 Н11.
| А1 = 17+0,13 | А5 = 11-0,013 |
| А2 = 170-0,25 | А6 = 28-0,13 |
| А3 = 17+0,13 | А7 = АСП |
| А4 = 22-0,16 (задан) | А8 = 22-0,16 (задан) |
| | |
Определяем координаты середин полей допусков составляющих звеньев размерной цепи:
| ЕсА = + 0,24 |  |
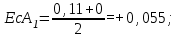 | 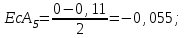 |
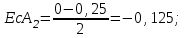 | 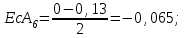 |
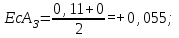 |  |
Определяем отклонения специального звена с целью совмещения верхних границ ESA’ и ESA:
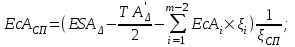
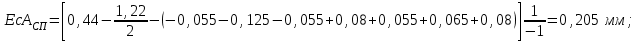
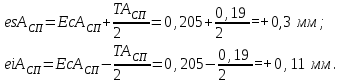
Таким образом, АСП.РАСЧ. =
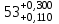 .
.Подбираем ближайшее стандартное значение основного отклонения
АСП =
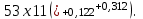
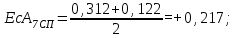
Уточняем расположение поля допуска ТА т.к. принятие стандартных предельных отклонений специального звена приведет к несовпадению верхних отклонений (ESAESA).
Так как прокладка-компенсатор является увеличивающим звеном размерной цепи:
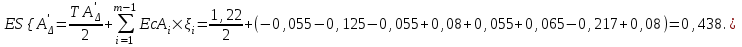
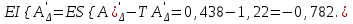
Определяем величину наибольшей возможной компенсации ТАк:
Так как прокладка-компенсатор, является увеличивающим звеном размерной цепи:
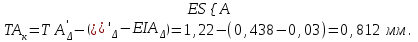
Определяем число ступеней компенсации, число и размер прокладок-компенсаторов.
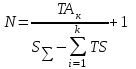
Так как величина требуемого зазора может меняться путем установки прокладки-компенсатора только в одно место собираемого узла, то суммарная толщина компенсатора (S) равна толщине одной прокладки (S) и может быть принятой равной допуску исходного звена (S=S= TA). Допуском на толщину прокладки можно пренебречь в связи с его малой численной величиной (по сравнению с допусками на составляющие звенья размерной цепи).
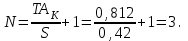
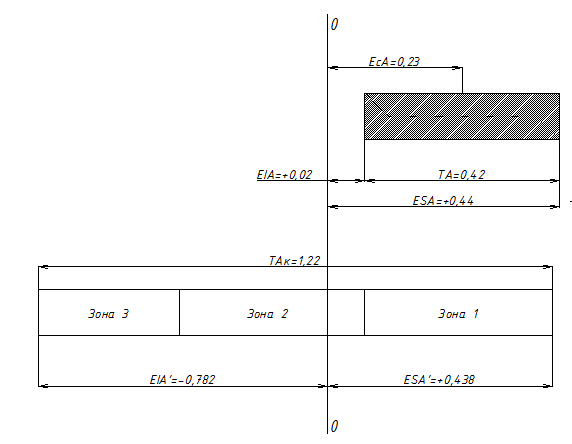
Составляем схему компенсации.
Вывод: требуемая точность исходного звена при расчетах методом регулирования достигается при следующих размерах составляющих звеньев:
| А1 = 17+0,11 | А5 = 11-0,11 |
| А2 = 170-0,25 | А6 = 28-0,13 |
| А3 = 17+0,13 | А7 =  |
| А4 = 22-0,16 (задан) | А8 = 22-0,16 (задан) |
В качестве звена-компенсатора использована прокладка толщиной S=0,42 мм. Компенсация производится следующим образом: если действительный размер А находится в зоне 1, то прокладка не ставится, если в зоне 2, то ставится одна прокладка, если в зоне 3, то две прокладки.
Метод регулирования обеспечивает требование средней экономической точности (все составляющие звенья изготавливаются по 11 квалитету).
Литература
1. А.И. Аристов, Л.И. Карпов, И.Д. Сергеев, Д.С. Фатюхин. Учебное пособие по курсу «Метрология, стандартизация, сертификация. Расчет размерных цепей». Издание 5-е переработанное и дополненное. М. - МАДИ, 2007.