Файл: Контрольная работа Основы теории информации и обработка данных средствами эвм вариант 1 Отчет студент гр.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 21
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство по рыболовству
Калининградский государственный технический университет
Факультет фундаментальной подготовки
Кафедра информатики и информационных технологий
Контрольная работа № <вставить текст>
Основы теории информации и обработка данных средствами ЭВМ
Вариант №1
Отчет
Выполнил: студент гр. <вставить текст>
И. О. Фамилия
«___» _____________2023 г.
Проверил: ст. преподаватель кафедры ИИТ,
Е. И. Константинова
г. Калининград, 2023
Оглавление
Цель работы 3
Приборы и материалы 3
Постановка задачи 3
Ход работы 4
Заключение 12
Список используемой литературы 13
Цель работы
Изучить основы теории информации, а также научиться обрабатывать различные данные средствами ЭВМ и такого ПО, как MS Excel и языка программирования Python.
Приборы и материалы
Персональный компьютер (ПК), Microsoft Excel, Microsoft Access, PyCharm IDE.
Постановка задачи
-
Записать число X(10) типа Double, используя представление с фиксированной и плавающей точкой. Выполнить проверку и сделать вывод о полученных результатах. -
Произвести сложение и умножение десятичных чисел X(10) и Y(10) в модифицированном обратном и дополнительном кодах. -
Построить таблицу истинности логической функции и записать ее СДНФ и СКНФ. -
Для каждой исходной последовательности классического кода Хэмминга (7;4) {r1r2i1r3i2i3i4} проверить, имеются ли ошибки. Написать исправленную последовательность. При отсутствии ошибок в ответ записать исходную последовательность. -
Используя шифр Цезаря и первый цикл алгоритма шифрования ГОСТ 28147 89 в режиме простой замены зашифруйте имена ученых, внесших огромный вклад в развитие теории информации. -
Оформить таблицы значений кусочно-непрерывной функции y(x) и поверхности z(x,y) и построить их график в MS Excel. -
Решить уравнение и систему линейных алгебраических уравнений в MS Excel. -
Используя статистические функции MS Excel, аппроксимировать экспериментальные данные зависимости некоторой величины y от х различными моделями. -
Создать базу данных (БД) предметной области своего варианта. С помощью запросов отобрать из БД требуемую информацию. Создать формы для ввода данных, отчеты и главную кнопочную форму. -
Для текстовой задачи составить блок-схему и реализовать ее на языке Python.
Ход работы
Задание 2. Произвести сложение и умножение десятичных чисел X(10) и Y(10) в модифицированном обратном и дополнительном кодах.
X = 67; Y = 41.
Модифицированные обратные и дополнительные коды получаются путём выделения на знак не одного, а двух бит. Для знака «+» это будет «00», для знака «-» - «11».
Последовательно преобразуем числа
| | Десятичная форма | Двоичная форма | Обратный код | Дополнительный код |
| X | +67 | +1000011 | 0,1000011 | 0,1000011 |
| Y | +41 | +101001 | 0,0101001 | 0,0101001 |
Обратный и дополнительный коды для положительных чисел совпадают с прямым кодом, поэтому 3, 4 и 5 столбцы идентичны.
| | Мод. Обр. код | Мод. Доп. код | | |
| X | 01,000011 | 01,000011 | | |
| Y | 00,101001 | 00,101001 | | |
Заметим, что при переводе числа 67 в модифицированный обратный и дополнительный коды возникает переполнение разрядной сетки («01» в битах, выделенных под знак). Это означает, что дальше с этим числом нельзя работать, так как будет получен неверный ответ. Поэтому вычислить сумму или произведение этих чисел в данных формах не предоставляется возможным. Число 41 при этом не переполняет разрядную сетку.
Задание 3. Построить таблицу истинности логической функции и записать ее СДНФ и СКНФ.
Логическая функция:
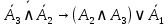
Таблица истинности:
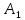 | 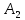 | 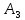 | 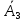 | 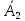 | 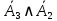 | 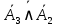 | 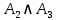 | 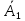 | 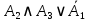 | ¬(¬c∧¬b)→(b∧c)∨¬a |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 |
Запись в СДНФ:
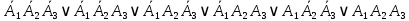
Запись в СКНФ:
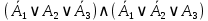
Задание 4. Для каждой исходной последовательности классического кода Хэмминга (7;4) {r1r2i1r3i2i3i4} проверить, имеются ли ошибки. Написать исправленную последовательность. При отсутствии ошибок в ответ записать исходную последовательность.
Исходная последовательность: {0101101}
Рассчитаем контрольные биты (r1, r2, r3):
r1 = i1 + i2 + i4 mod 2 = 0
r2 = i1 + i3 + i4 mod 2 = 1
r3 = i2 + i3 + i4 mod 2 = 0
Сформировав новую последовательность {r1r2i1r3i2i3i4} = 0100101, заметим, что контрольный бит 3 не совпадает, следовательно, его нужно инвертировать. Результат: 0100101.
Задание 6. Оформить таблицы значений кусочно-непрерывной функции y(x) и поверхности z(x,y) и построить их график в MS Excel.
Кусочно-непрерывная функция:
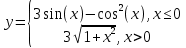
Функция поверхности:
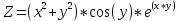
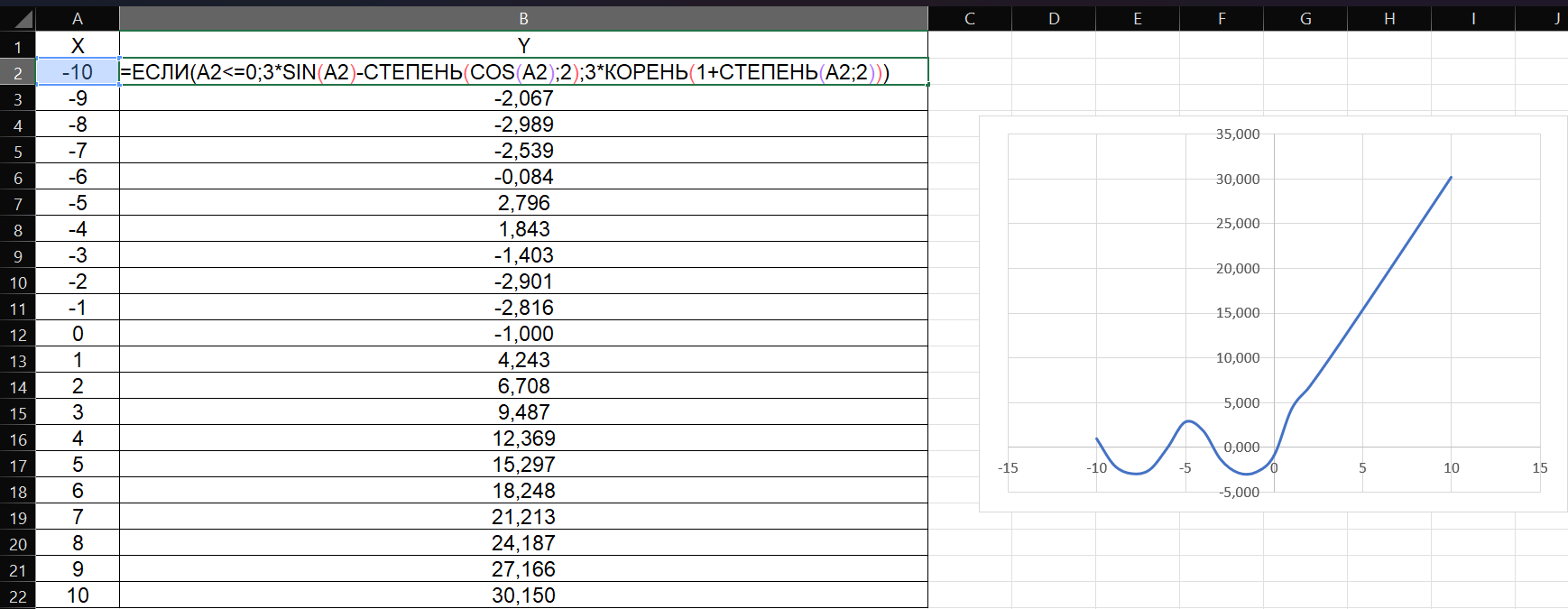
Рис. 1. Данные и график кусочно-непрерывной функции
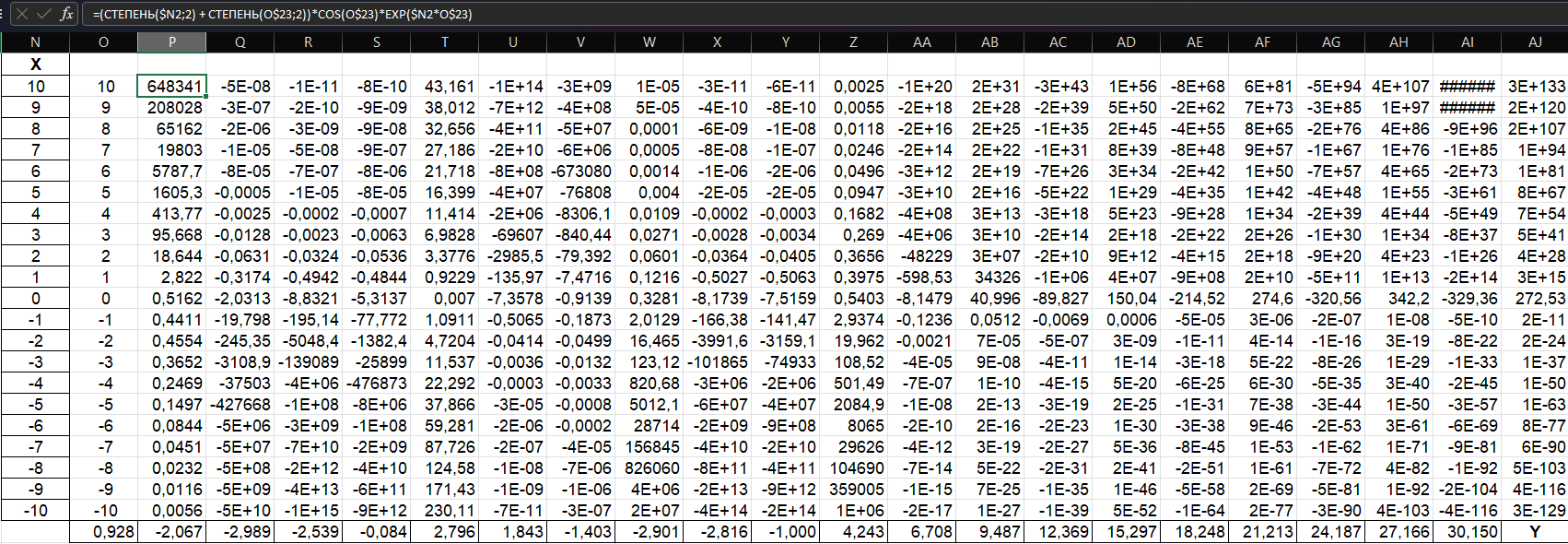
Рис. 2. Данные функции поверхности
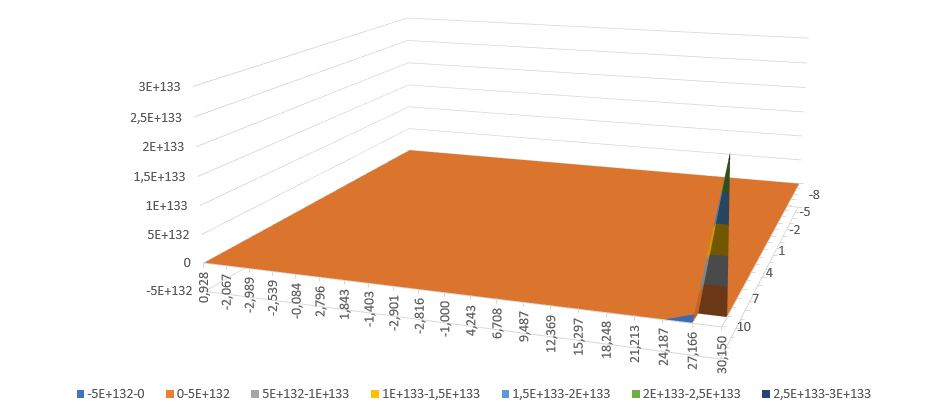
Рис. 3. График функции поверхности
Задание 7. Решить уравнение и систему линейных алгебраических уравнений в MS Excel.
Уравнение:
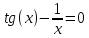
Построим график функции
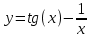 . Заметим, что данный график будет пересекать ось абсцисс бесконечное число раз, поэтому для данного задания найдём корни на интервале от -2 до 4 (4 пересечения)
. Заметим, что данный график будет пересекать ось абсцисс бесконечное число раз, поэтому для данного задания найдём корни на интервале от -2 до 4 (4 пересечения)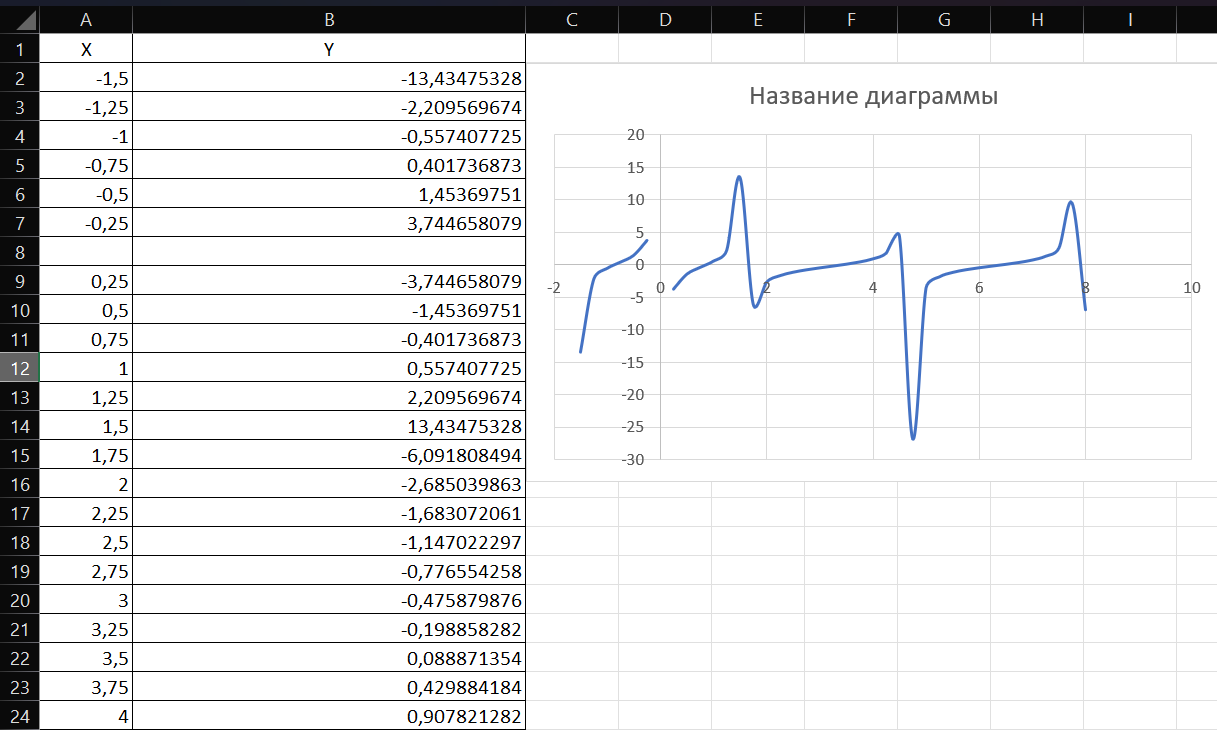
Рис. 4. Данные и график функции
Запишем во второй столбец приближённые значения x, основываясь на графике. Далее, в третьем столбце вызываем метод «Подбор параметра» и устанавливаем для каждой строки искомое значение «0» и задаём для перебора соответствующую ячейку второго столбца. Делаем так со всеми остальными корнями и находим приближённый результат.
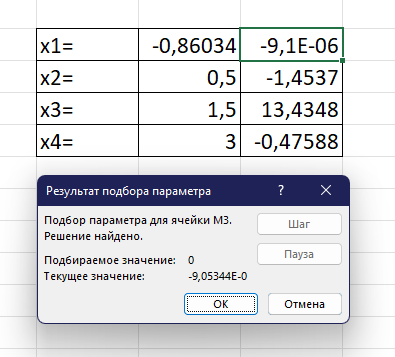
Рис. 5. Окно с результатом подбора для x1
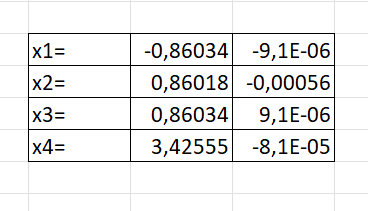
Рис. 6. Результат использования метода «Подбор параметра»
Теперь решим СЛАУ. Будем использовать метод Крамера.
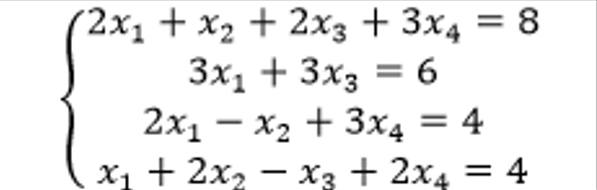
Рис. 7. Условие СЛАУ
Заполним основную и вспомогательные матрицы данными. Для каждой из матриц A, A1, A2, A3, A4 необходимо вычислить определители d, d1, d2, d3, d4. Для этого последовательно в каждую ячейку H6:H10 впишем функцию МОПРЕД и в качестве параметра укажем соответствующую матрицу. Далее, согласно методу Крамера, разделим каждый определитель вспомогательной матрицы на определитель главной матрицы. Результат в каждом случае – 1, следовательно СЛАУ имеет решение (1, 1, 1, 1).
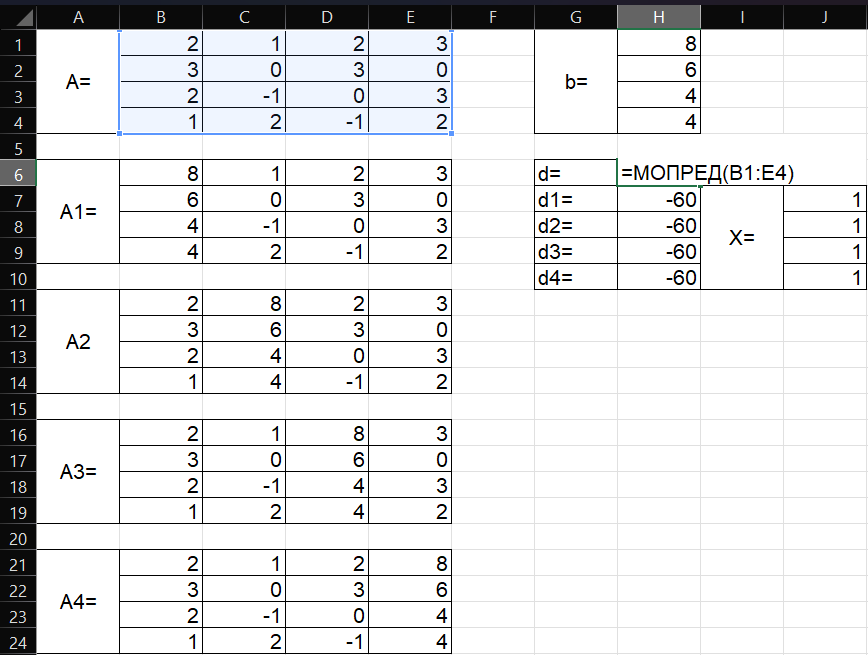
Рис. 8. Решение СЛАУ методом Крамера
Задание 8. Используя статистические функции MS Excel, аппроксимировать экспериментальные данные зависимости некоторой величины y от х различными моделями.
Экспериментальные данные:
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| y | 35,6 | 38,7 | 39,4 | 40,8 | 43,3 | 42,9 | 41,8 | 41,4 | 40,2 | 38,3 |
Для аппроксимирования были использованы функции ТЕНДЕНЦИЯ (линейный тренд), РОСТ (экспоненциальный тренд). Также, для определения параметров каждой зависимости были использованы функции ЛГРФПРИБЛ, ЛИНЕЙН.

Рис. 9. Ввод нужных формул в ячейки
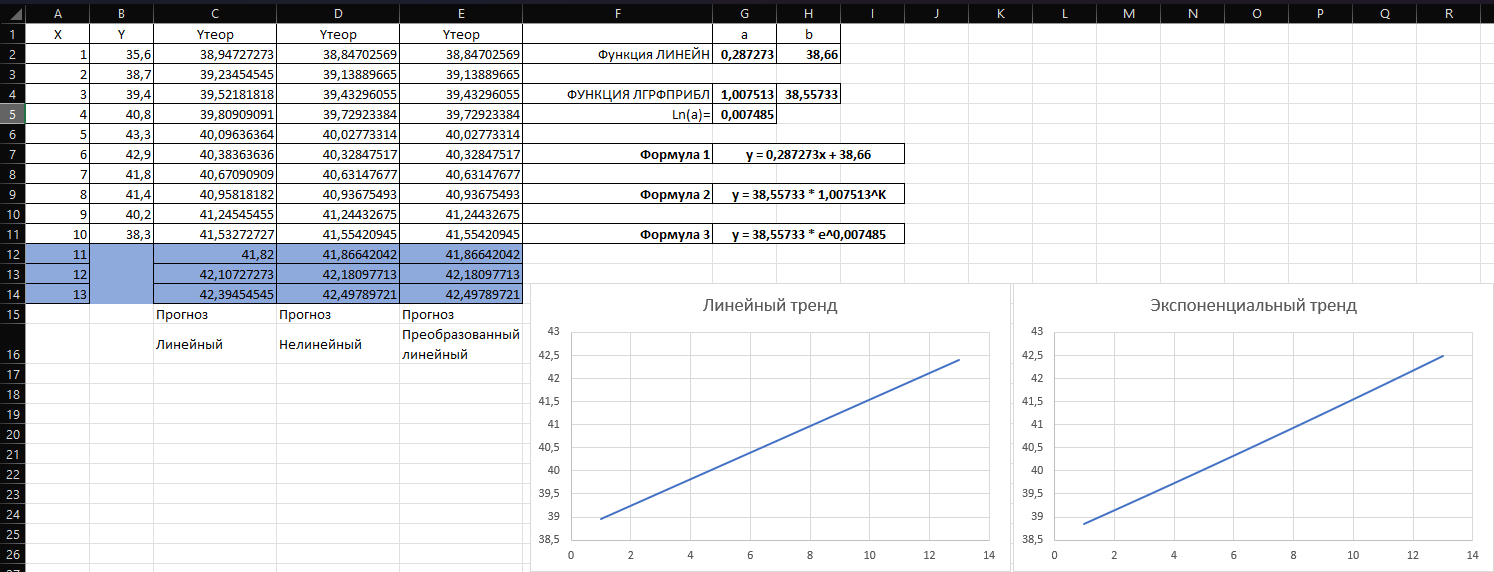
Рис. 10. Результаты аппроксимирования различными способами
Задание 10.
Для следующей задачи составить блок-схему и реализовать ее на языке Python: Даны два натуральных числа m и n (m ≤ 9999, n ≤ 9999). Проверить, есть ли в записи числа m цифры, одинаковые с цифрами в записи числа n.
Блок-схема:
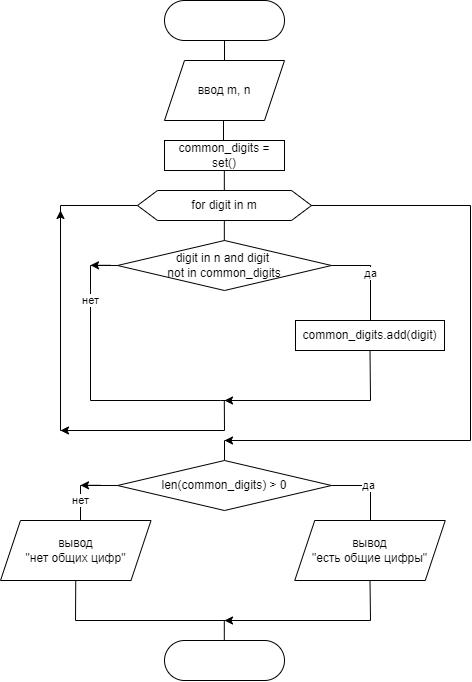
Рис. 11. Блок-схема алгоритма для решения задачи
Программный код:
m = input("Введите первое число: ")
n = input("Введите второе число: ")
common_digits = set()
for digit in m:
if digit in n and digit not in common_digits:
if len(common_digits) > 0:
print("В числах {} и {} есть общие цифры: {}".format(m, n, common_digits))
else:
print("В числах {} и {} нет общих цифр".format(m, n))
Программа получает на вход два числа: m и n. Далее создаётся список типа set (в таком списке элементы не повторяются). После этого в цикле for программа проходит по каждой цифре из числа m, и если условие проверки (данная цифра есть в числе n и её нет в списке common_digits) выполняется, то текущая цифра добавляется в список common_digits. В конце, если список common_digits не пустой, выдаётся сообщение о наличии общих цифр, иначе выдаётся сообщение об отсутствии таких цифр.
Результат:
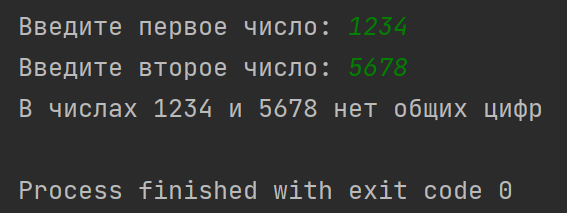
Рис. 12. Результат работы программного кода с отсутствием общих цифр
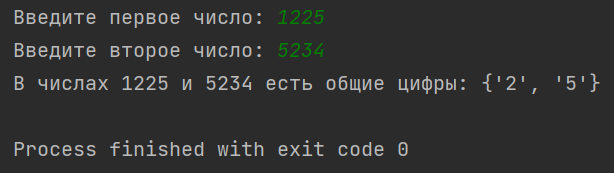
Рис. 13. Результат работы программного кода с наличием общих цифр