Файл: Курсовая работа по дисциплине Технологии обработки информации Вариант 3 Фамилия Мельник.docx

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ

УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)
ИНСТИТУТ ‏ㅤ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ

КУРСОВАЯ РАБОТА
по дисциплине

«Технологии обработки информации»
Вариант 3


Фамилия: Мельник

Имя: Владимир

Отчество: Николаевич

Группа: №: ИБ-04з

Санкт-Петербург

2023

Оглавление

Введение

Курсовая работа выполняется в рамках образовательной программы «Информационные системы и технологии» («Интеллектуальные системы и технологии») и является неотъемлемой частью образовательного процесса. Выполнение курсовой работы представляет собой решение студентом, под руководством преподавателя, конкретных задач обработки информации.

Цель курсовой работы – углубить знания и умения студентов, полученные в процессе теоретических и практических занятий, улучшить навыки самостоятельного поиска и изучения материала по теме курсовой работы, а также развить компетенции аналитической, исследовательской и проектной деятельности. В частности, компетенции:

- ПК-1 - способность проводить исследования на всех этапах жизненного цикла программных средств;

- ПК-18 - способность выполнять работы по созданию (модификации) и сопровождению ИС, автоматизирующих задачи организационного управления и бизнес-процессы;

- ПК-19 - способность выполнять работы и управлять работами по созданию (модификации) и сопровождению ИС, автоматизирующих задачи организационного управления и бизнес-процессы.

---

Задание №1 Понижение размерности данных

Исследовать эффективность методов PCA и SVD для понижения размерности данных.

В качестве исходных данных для анализа следует самостоятельно выбрать изображение в формате jpg. Размер изображения должен быть не менее 400 х 400 пикселей.

В ходе исследования необходимо проделать следующее:

- выбрать и обосновать количество главных компонент, достаточное для качественной визуализации;

- оценить выигрыш сжатого изображения по объему, по сравнению с оригиналом;

- оценить количество «утраченной» информации;

- выяснить зависит ли достаточное число компонент для качественной визуализации от характера изображения (если да, то оценить эту зависимость)

Загрузка и подготовка исходных данных для анализа

Для текущей работы было выбрано изображение в формате jpg размером 750 х 750 пикселей, содержащее яркое изображение, представлено на рисунке 1.



Рисунок 1. Исходное изображение для алгоритма PCA и SVD

Согласно предложенному алгоритму подготовки данных исходное изображение было прочитано и конвертировано в матрицу, хранящую представление исходного изображения в оттенках серого. Сделано это было для того, чтобы исключить цветные каналы изображения, которые для данной задачи не имеют принципиального значения.
library(imager)

library(gcookbook)
#прописываем путь до картинки и читаем изображение с рабочего директория

image_name = '/Users/Desktop/БОНЧ 2022-2023 учебный год/Курсовой ТОИ/Мельник/zadanie1/image.jpg1'

im <- load.image(image_name)
#переводим в черно-белое представление

x <- grayscale(im)

plot(x)

Листинг 1

Изображение представлено на рисунке 2.



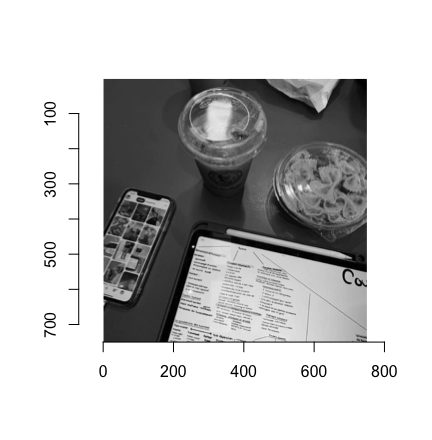
Рисунок 2. Изображение в оттенках серого

Главные теоретические положения

Метод главных компонент — это технология многомерного статистического анализа, используемая для сокращения размерности пространства признаков с минимальной потерей полезной информации. Предложен K. Пирсоном в 1901 г., а затем детально разработан американским экономистом и статистиком Г. Хоттелингом.

С математической точки зрения метод главных компонент представляет собой ортогональное линейное преобразование, которое отображает данные из исходного пространство признаков в новое пространство меньшей размерности.

---

При этом первая ось новой системы координат строится таким образом, чтобы дисперсия данных вдоль неё была бы максимальна. Вторая ось строится ортогонально первой так, чтобы дисперсия данных вдоль неё, была бы максимальной их оставшихся возможных и т.д. Первая ось называется первой главной компонентой, вторая — второй и т.д.

смысл метода заключается в том, что с каждой главной компонентой связана определённая доля общей дисперсии исходного набора данных (её называют нагрузкой). В свою очередь, дисперсия, являющаяся мерой изменчивости данных, может отражать уровень их информативности.

Действительно, вдоль некоторых осей исходного пространства признаков изменчивость может быть большой, вдоль других — малой, а вдоль третьих вообще отсутствовать. Предполагается, что чем меньше дисперсия данных вдоль оси, тем менее значим вклад переменной, связанной с данной осью и, следовательно, исключив эту ось из пространства (т.е. переменную из модели), можно уменьшить размерность задачи почти не проиграв в информативности данных.

Следовательно, задача метода главных компонент заключается в том, чтобы построить новое пространство признаков меньшей размерности, дисперсия между осями которой будет перераспределена так, чтобы максимизировать дисперсию по каждой из них. Для этого выполняется последовательность следующих действий:

1. 
   Вычисляется общая дисперсия исходного пространства признаков. Это нельзя сделать простым суммированием дисперсий по каждой переменной, поскольку они, в большинстве случаев, не являются независимыми. Поэтому суммировать нужно взаимные дисперсии переменных, которые определяются из ковариационной матрицы.
   
2. 
   Вычисляются собственные векторы и собственные значения ковариационной матрицы, определяющие направления главных компонент и величину связанной с ними дисперсии.
   
3. 
   Производится снижение размерности. Диагональные элементы ковариационной матрицы показывают дисперсию по исходной системе координат, а её собственные значения — по новой. Тогда разделив дисперсию, связанную с каждой главной компонентой на сумму дисперсий по всем компонентам, получаем долю дисперсии, связанную с каждой компонентой. После этого отбрасывается столько главных компонент, чтобы доля оставшихся составляла 80-90%.
   

Решение поставленной задачи

Главные компоненты в работе вычисляются, используя сингулярное разложение матриц. Эта функция svd вычисляет три матрицы S, U и V сингулярного разложения.

---

image_data=as.matrix(x)

data.svd = svd(image_data)

d = diag(data.svd$d)

#Определяем размерность

dim(d)
#сингулярный спектр

U=data.svd$u

V=data.svd$v

Листинг 2

Их используют как основу и выбирают из них разное число главных компонент k, формируя сжатые изображения. Сделать это можно в цикле, как показано в листинге 3.

#Готовим формат вывода - 2 строки по 2 изображения

par(mfrow=c(2,2))

#Формируем изображения с использованием 4-х различных k

for (k in c(5,20,50,250))

{

us <- as.matrix(U[, 1:k])

vs <- as.matrix(V[, 1:k])

ds <- as.matrix(d[1:k, 1:k])

ls <- us %*% ds %*% t(vs)

lsg <- as.cimg(ls)

#визуализируем каждое полученное изображение

plot(0:2, type='n')

rasterImage(lsg,1,0,3,2)

imager::save.image(lsg,paste("/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год /Курсовой ТОИ/Мельник/zadanie1/",k,".jpg"))

}

Листинг 3

В результате получается 4 изображения с разным количеством главных компонент и соответственно с разным качество, которые представлены на рисунке 3.



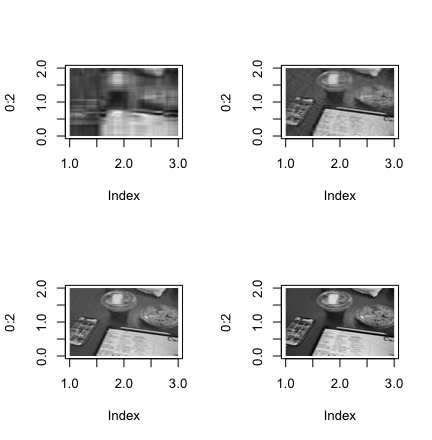
Рисунок 3. Изображения с разным количеством главных компонент (5,20,50,250)

Программный код

# библиотеки

install.packages("imager")

install.packages("gcookbook")

library(imager)

library(gcookbook)
#прописываем путь до картинки и читаем изображение с рабочего директория

image_name = '/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie1/image.jpg'

im <- load.image(image_name)
#переводим в черно-белое представление

x <- grayscale(im)

plot(x)
image_data=as.matrix(x)

data.svd = svd(image_data)

d = diag(data.svd$d)

#Определяем размерность

dim(d)
#сингулярный спектр

U=data.svd$u

V=data.svd$v
#Готовим формат вывода - 2 строки по 2 изображения

par(mfrow=c(2,2))

#Формируем изображения с использованием 4-х различных k

for (k in c(5,20,50,250))

{

us <- as.matrix(U[, 1:k])

vs <- as.matrix(V[, 1:k])

ds <- as.matrix(d[1:k, 1:k])

ls <- us %*% ds %*% t(vs)

lsg <- as.cimg(ls)

#визуализируем каждое полученное изображение

plot(0:2, type='n')

rasterImage(lsg,1,0,3,2)

imager::save.image(lsg,paste("/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie1/",k,".jpg"))

}
original <- file.info(image_name)$size / 1000

imgs <- dir('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie1')
for (i in imgs) {

full.path <- paste('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie/', i, sep='')

print(full.path)

print(paste(i, ' size: ', file.info(full.path)$size / 1000, ' original: ', original, ' % diff: ', round((file.info(full.path)$size / 1000 - original) / original, 2) * 100, '%', sep = ''))

}

Заключение

В данном задании были получены практические навыки в работе с алгоритмами понижения размерности PCA и SVD на примере задачи сжатия изображения.

---

Список использованных источников

1. 
   Филиппов Ф.В., Технологии обработки информации, методическое пособие для курсовой работы, СПб., 2021. – 27
   
2. 
   Метод главных компонент (примеры на R) http://math-info.hse.ru/f/2015-16/ling-magquant/lecture-pca.html
   

Контрольные вопросы

1) Как вычислить матрицу счетов метода РСА исследуемой матрицы Х, используя сингулярное разложение Х?

Суть метода главных компонент – существенное понижение размерности данных. Исходная матрица X заменяется двумя новыми матрицами T и P:



Матрица T называется матрицей счетов (scores), а матрица P — матрицей нагрузок (loadings). Использование сингулярного разложения подразумевает представление исходной матрицы X на 3 матрицы



если в матрице S оставить только k наибольших сингулярных значений, а в матрицах U и V только соответствующие этим значениям столбцы, то произведение получившихся матриц будет наилучшим приближением исходной матрицы X к матрице меньшего ранга k.

Связь между PCA и SVD выражается соотношениями, позволяющими ответить на исходный вопрос.



2) Опишите процесс выделения главных компонент в многомерном случае своими словами.

В многомерном случае, процесс выделения главных компонент происходит так:

1. 
   Ищется центр облака данных, и туда переносится новое начало координат – это нулевая главная компонента.
   
2. 
   Выбирается направление максимального изменения данных – это первая главная компонента.
   
3. 
   Если данные описаны не полностью (шум велик), то выбирается еще одно направление – перпендикулярное к первому, так чтобы описать оставшееся изменение в данных и т.д.
   

3) Что такое собственные значения матрицы счетов метода РСА и что они характеризуют?

Пусть A — это квадратная матрица. Вектор v называется собственным вектором матрицы A, если 

Av = λv,

где число λ называется собственным значением матрицы A. Таким образом преобразование, которое выполняет матрица A над вектором v, сводится к простому растяжению или сжатию с коэффициентом λ. Собственный вектор определяется с точностью до умножения на константу α ≠ 0, т.е. если 

---