Файл: Курсовая работа по дисциплине Технологии обработки информации Вариант 3 Фамилия Мельник.docx
Добавлен: 04.12.2023
Просмотров: 126
Скачиваний: 12
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Задание №1 Понижение размерности данных
Загрузка и подготовка исходных данных для анализа
Главные теоретические положения
Список использованных источников
Задание №2 Кластеризация данных
Загрузка и подготовка исходных данных для анализа
Главные теоретические положения
Список использованных источников
Задание №3 Обработка графической информации
v — собственный вектор, то и αv — тоже собственный вектор.
У матрицы A, размерностью (N×N) не может быть больше, чем N собственных значений. Они удовлетворяют характеристическому уравнению
det(A − λI) = 0,
являющемуся алгебраическим уравнением N-го порядка.
4) Как связаны между собой сингулярные значения SVD разложения и собственные значения матрицы счетов метода РСА?
Метод главных компонент тесно связан с другим разложением – по сингулярным значениям, SVD. В последнем случае исходная матрица X разлагается в произведение трех матриц:
X=USVt
Здесь U – матрица, образованная ортонормированными собственными векторами ur матрицы XXt, соответствующим значениям λr:
XXtur = λrur
V – матрица, образованная ортонормированными собственными векторами vr матрицы XtX:
XtXvr = λrvr
S – положительно определенная диагональная матрица, элементами которой являются сингулярные значения σ1≥... ≥σR≥0 равные квадратным корням из собственных значений λr
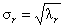
Связь между PCA и SVD определяется следующими простыми соотношениями:
T = US P = V
5) Какие критерии выбора числа главных компонент используются на практике?
Задача метода главных компонент заключается в том, чтобы построить новое пространство признаков меньшей размерности, дисперсия между осями которой будет перераспределена так, чтобы максимизировать дисперсию по каждой из них. Для этого выполняется последовательность следующих действий:
Исследовать возможности классификации данных с использованием алгоритмов t-SNE и UMAP.
Исходные данные для анализа загрузить из ресурса Wine Quality (http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality) репозитария. Варианты заданий (номер варианта определяется последней цифрой номера зачетки) приведены в табл. 1.
Таблица 1

Анализируемые данные включают 11 объективных параметров различных сортов вина:
- фиксированная кислотность;
- летучая кислотность;
- лимонная кислота;
- остаточный сахар;
- хлориды;
- свободный диоксид серы;
- общий диоксид серы;
- плотность;
- pH;
- сульфаты;
- спирт.
Последний, 12-ый параметр является субъективной оценкой качества, проставляемой экспертом, и имеет несколько градаций.
Основная задача исследования состоит в определении качества субъективной оценки экспертов и формированию обоснованной кластеризации вин.
Исследование должно содержать:
- описание исследуемого набора данных,
- подготовку данных для анализа,
- план и решаемые задачи,
- выбор используемых функций и описание их параметров,
- результаты исследования,
- аргументированные выводы.
Программный код должен быть снабжен подробным комментарием.
Согласно варианту задания был загружен датасет оценки качества красного вина. Реализовано это было с помощью функции чтения данных, разделенных разделителем, в данном случае символом точки с запятой read.delim. После этого необходимо было определить фактором столбец качества вина.
library("readr")
library("Rtsne")
library("magrittr")
library("data.table")
library("dplyr")
library("ggplot2")
library("umap")
#чтение файла
data <- read.delim('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie2/winequality-white.csv', sep=';')
#определить фактором столбец качества вина
data$quality <- factor(data$quality, ordered = T)
#задаем начальную фазу генератора случайных чисел - для воспроизводимости
set.seed(1)
#подготовка визуализации графиков в 2 строки по 2 графика
par(mfrow=c(2,2))
Листинг 4
Поскольку данные не содержали пропусков или прочих некорректных данных, то последним шагом в подготовке их к работе с алгоритмами кластеризации было перемешивание и определение обучающей выборки.

Эта операция идентичная как для tSNE так и для UMAP
t-распределенное стохастическое соседнее вложение t-SNE (t-Distributed Stochastic Neighbor Embedding) — это алгоритм нелинейного уменьшения размерности, используемый для исследования данных большой размерности [1]. Он отображает многомерные данные в двух или более измерениях, подходящих для наблюдения человеком. Алгоритм t-SNE (2008), в ряде случаев намного эффективнее PCA (1933). Важно подчеркнуть, что большинство нелинейных методов, кроме t-SNE, не способны одновременно сохранять локальную и глобальную структуру данных [5].
SNE начинается с преобразования многомерной евклидовой дистанции между точками в условные вероятности, отражающие сходство точек. Математически это выглядит следующим образом:
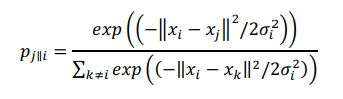 (4)
(4)
Формула (4) показывает, насколько точка xj близка к точке xi при гауссовом распределении вокруг xi с заданным отклонением σ. Сигма будет различной для каждой точки. Она выбирается так, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется оценка перплексии (perplexity):
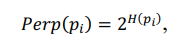 (5)
(5)
г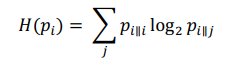 де
де
- энтропия Шеннона (6)
После генерации обучающей выборки следующим этапом было проверить работу алгоритма для разных значений перплексии.
#организуем цикл для 4-х значений реплексии
for (k in c(5,10,25,50)) {
res.tsne <- Rtsne(data[,-1], dims=2, perplexity=k, verbose=TRUE, max_iter=500,check_duplicates=FALSE)
colors = rainbow(length(unique(data$quality)))
plot(res.tsne$Y, t='n', main=paste('tSNE::per',k), xlab='tSNE dim 1', ylab='tSNE dim 2')
text(res.tsne$Y, labels=data$quality, col=colors[data$quality])
print('======')
}
Листинг 5
Кластеры должны окрашиваться в то количество цветов, которое совпадает с количеством уникальных значений в факторном столбце. Текущий цикл перебирает значения перплексии [5, 10, 25, 50] и графический результат представлен на рисунке 4.
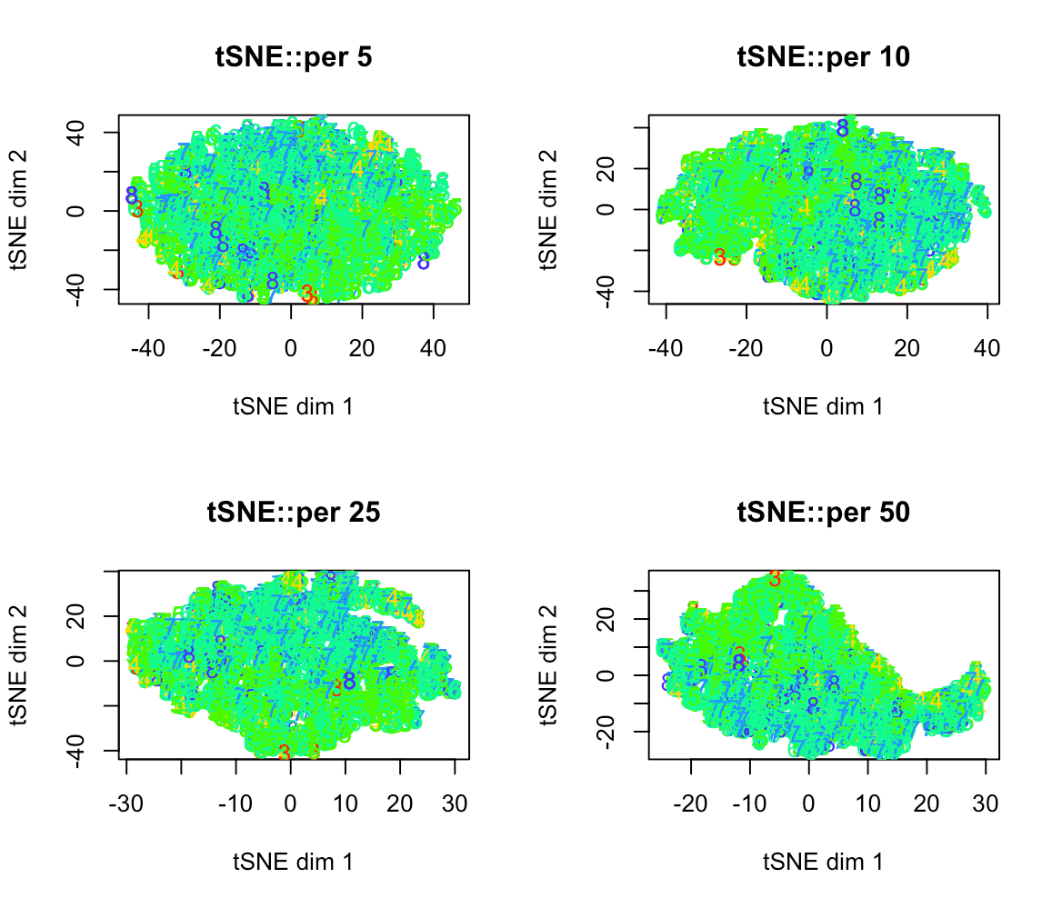
Рисунок 4. Вид кластеров tSNE при различной перплексии
Если рассматривать отдельно результат кластеризации
, например для значения перплексии 50, можно увидеть, что присутствует динамика в сторону увеличения похожих на полноценные кластеры совокупностей точек, что в свою очередь может свидетельствовать о положительной возможности использовать алгоритм понижения размерности tSNE в задачах кластеризации и в искомом датасете в частности.
Для алгоритма UMAP последовательность действий, по сути, такая же, после формирования обучающей выборки вызвать функцию umap из пакета umap.
#UMAP
rows.umap <- sample(1:nrow(data), nrow(data)*0.7)
data.umap <- data[rows.umap,]
res.umap <- umap(data.umap[,-ncol(data.umap)])
colors=rainbow(10)
par(mfrow=c(1,1))
plot(res.umap$layout, t='n', main='UMAP wine Q', xlab='UMAP dim 1', ylab='UMAP dim 2',
'cex.main'=2, 'cex.lab'=1.5)
text(res.umap$layout, labels=data$quality, col=colors[data$quality])
Листинг 6
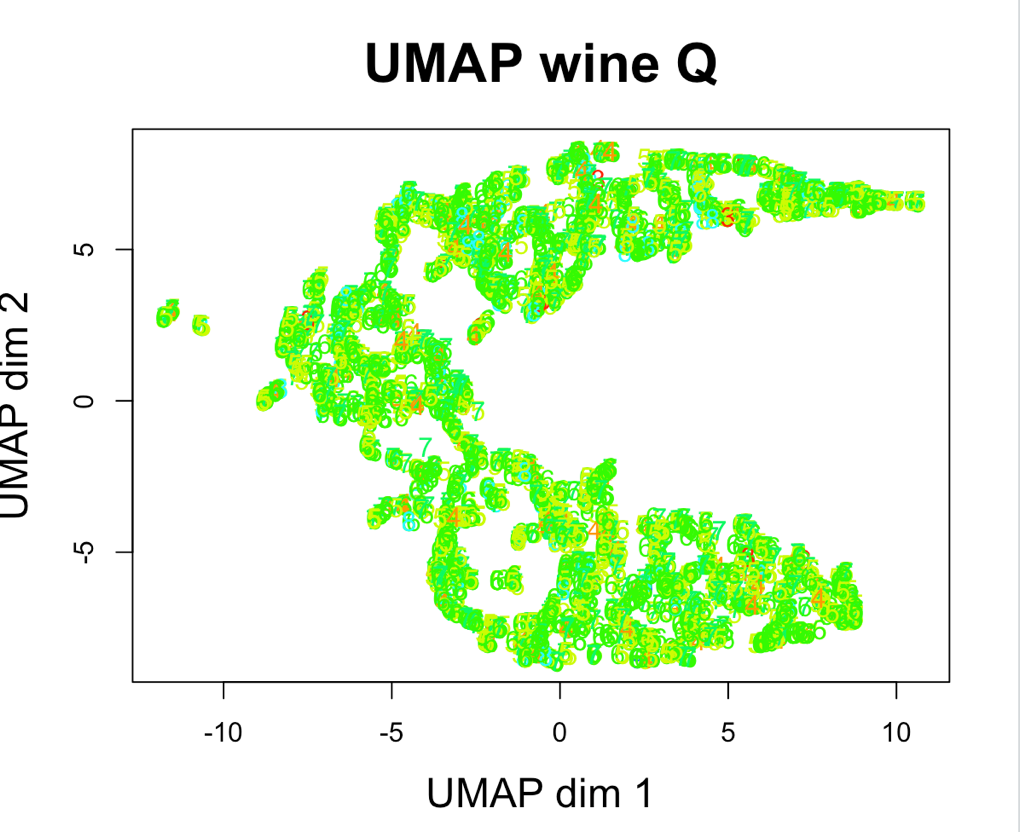
Рисунок 5. Вид кластеров UMAP
В итоге есть основания утверждать, что оба алгоритма при правильно подобранных параметрах и предварительно проверенных на корректность данных являются применимыми в задачах кластеризации.
install.packages("readr")
install.packages("Rtsne")
install.packages("magrittr")
install.packages("data.table")
install.packages("dplyr")
install.packages("ggplot2")
install.packages("umap")
library("readr")
library("Rtsne")
library("magrittr")
library("data.table")
library("dplyr")
library("ggplot2")
library("umap")
#чтение файла
data <- read.delim('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie2/winequality-white.csv', sep=';')
#определить фактором столбец качества вина
data$quality <- factor(data$quality, ordered = T)
#задаем начальную фазу генератора случайных чисел - для воспроизводимости
set.seed(1)
#подготовка визуализации графиков в 2 строки по 2 графика
par(mfrow=c(2,2))
#перемешивание и определение обучающей выборки
rows.tsne <- sample(1:nrow(data), nrow(data)*0.7)
#организуем цикл для 4-х значений реплексии
for (k in c(5,10,25,50)) {
res.tsne <- Rtsne(data[,-1], dims=2, perplexity=k, verbose=TRUE, max_iter=500,check_duplicates=FALSE)
colors = rainbow(length(unique(data$quality)))
plot(res.tsne$Y, t='n', main=paste('tSNE::per',k), xlab='tSNE dim 1', ylab='tSNE dim 2')
text(res.tsne$Y, labels=data$quality, col=colors[data$quality])
print('======')
}
#UMAP
rows.umap <- sample(1:nrow(data), nrow(data)*0.7)
data.umap <- data[rows.umap,]
res.umap <- umap(data.umap[,-ncol(data.umap)])
colors=rainbow(10)
par(mfrow=c(1,1))
plot(res.umap$layout, t='n', main='UMAP wine Q', xlab='UMAP dim 1', ylab='UMAP dim 2',
'cex.main'=2, 'cex.lab'=1.5)
text(res.umap$layout, labels=data$quality, col=colors[data$quality])
В данном разделе были получены теоретические знания и практические навыке в работе с алгоритмами понижения размерности tSNE и UMAP в задачах кластеризации.
1) Как можно интерпретировать назначение и выбирать адекватное значение перплексии при использовании алгоритма t-SNE?
Перплексия может быть интерпретирована как сглаженная оценка эффективного количества «соседей» для точки xi. Она задается в качестве параметра метода t-SNE и рекомендуется использовать ее значение в интервале от 5 до 50. Сигма определяется для каждой пары xi и xj при помощи алгоритма бинарного поиска.
2) Как решается проблема скученности точек в пространстве отображения в алгоритме t-SNE?
Использование классического SNE позволяет получить неплохие результаты, но может быть связано с трудностями в оптимизации функции потерь и проблемой скученности (в оригинале – crowding problem). t-SNE если и не решает эти проблемы совсем, то существенно облегчает. Функция потерь t-SNE имеет два принципиальных отличая. Во-первых, у t-SNE симметричная форма сходства в многомерном пространстве и более простой вариант градиента. Во-вторых, вместо гауссова распределения для точек из пространства отображения используется t-распределение (Стьюдента), «тяжелые» хвосты которого облегчают оптимизацию и решают проблему скученности. [2]
3) Чем распределение Стьюдента отличается от нормального распределения?
Форма распределения Стьюдента похожа на форму нормального распределения. Отличием является то, что «хвосты» распределения Стьюдента медленнее стремятся к нулю, чем «хвосты» нормального распределения.
4) Что пытается сохранить алгоритм UMAP: глобальную структуру анализируемых данных или локальные расстояния между отдельными точками?
Алгоритм UMAP относится к группе алгоритмов, которые пытаются сохранить локальные расстояния между отдельными точками, в отличие от PCA.
Визуализировать отрывок сказки К.И.Чуковского «Муха-цокотуха» с использованием технологии SVG, соответствующий номеру фрагмента. Номер своего фрагмента определяется последней цифрой номера зачетной книжки:
У матрицы A, размерностью (N×N) не может быть больше, чем N собственных значений. Они удовлетворяют характеристическому уравнению
det(A − λI) = 0,
являющемуся алгебраическим уравнением N-го порядка.
4) Как связаны между собой сингулярные значения SVD разложения и собственные значения матрицы счетов метода РСА?
Метод главных компонент тесно связан с другим разложением – по сингулярным значениям, SVD. В последнем случае исходная матрица X разлагается в произведение трех матриц:
X=USVt
Здесь U – матрица, образованная ортонормированными собственными векторами ur матрицы XXt, соответствующим значениям λr:
XXtur = λrur
V – матрица, образованная ортонормированными собственными векторами vr матрицы XtX:
XtXvr = λrvr
S – положительно определенная диагональная матрица, элементами которой являются сингулярные значения σ1≥... ≥σR≥0 равные квадратным корням из собственных значений λr
Связь между PCA и SVD определяется следующими простыми соотношениями:
T = US P = V
5) Какие критерии выбора числа главных компонент используются на практике?
Задача метода главных компонент заключается в том, чтобы построить новое пространство признаков меньшей размерности, дисперсия между осями которой будет перераспределена так, чтобы максимизировать дисперсию по каждой из них. Для этого выполняется последовательность следующих действий:
-
Вычисляется общая дисперсия исходного пространства признаков. Это нельзя сделать простым суммированием дисперсий по каждой переменной, поскольку они, в большинстве случаев, не являются независимыми. Поэтому суммировать нужно взаимные дисперсии переменных, которые определяются из ковариационной матрицы. -
Вычисляются собственные векторы и собственные значения ковариационной матрицы, определяющие направления главных компонент и величину связанной с ними дисперсии. -
Производится снижение размерности. Диагональные элементы ковариационной матрицы показывают дисперсию по исходной системе координат, а её собственные значения — по новой. Тогда разделив дисперсию, связанную с каждой главной компонентой на сумму дисперсий по всем компонентам, получаем долю дисперсии, связанную с каждой компонентой. После этого отбрасывается столько главных компонент, чтобы доля оставшихся составляла 80-90%.
Задание №2 Кластеризация данных
Исследовать возможности классификации данных с использованием алгоритмов t-SNE и UMAP.
Исходные данные для анализа загрузить из ресурса Wine Quality (http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality) репозитария. Варианты заданий (номер варианта определяется последней цифрой номера зачетки) приведены в табл. 1.
Таблица 1

Анализируемые данные включают 11 объективных параметров различных сортов вина:
- фиксированная кислотность;
- летучая кислотность;
- лимонная кислота;
- остаточный сахар;
- хлориды;
- свободный диоксид серы;
- общий диоксид серы;
- плотность;
- pH;
- сульфаты;
- спирт.
Последний, 12-ый параметр является субъективной оценкой качества, проставляемой экспертом, и имеет несколько градаций.
Основная задача исследования состоит в определении качества субъективной оценки экспертов и формированию обоснованной кластеризации вин.
Исследование должно содержать:
- описание исследуемого набора данных,
- подготовку данных для анализа,
- план и решаемые задачи,
- выбор используемых функций и описание их параметров,
- результаты исследования,
- аргументированные выводы.
Программный код должен быть снабжен подробным комментарием.
Загрузка и подготовка исходных данных для анализа
Согласно варианту задания был загружен датасет оценки качества красного вина. Реализовано это было с помощью функции чтения данных, разделенных разделителем, в данном случае символом точки с запятой read.delim. После этого необходимо было определить фактором столбец качества вина.
library("readr")
library("Rtsne")
library("magrittr")
library("data.table")
library("dplyr")
library("ggplot2")
library("umap")
#чтение файла
data <- read.delim('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie2/winequality-white.csv', sep=';')
#определить фактором столбец качества вина
data$quality <- factor(data$quality, ordered = T)
#задаем начальную фазу генератора случайных чисел - для воспроизводимости
set.seed(1)
#подготовка визуализации графиков в 2 строки по 2 графика
par(mfrow=c(2,2))
Листинг 4
Поскольку данные не содержали пропусков или прочих некорректных данных, то последним шагом в подготовке их к работе с алгоритмами кластеризации было перемешивание и определение обучающей выборки.

Эта операция идентичная как для tSNE так и для UMAP
Главные теоретические положения
t-распределенное стохастическое соседнее вложение t-SNE (t-Distributed Stochastic Neighbor Embedding) — это алгоритм нелинейного уменьшения размерности, используемый для исследования данных большой размерности [1]. Он отображает многомерные данные в двух или более измерениях, подходящих для наблюдения человеком. Алгоритм t-SNE (2008), в ряде случаев намного эффективнее PCA (1933). Важно подчеркнуть, что большинство нелинейных методов, кроме t-SNE, не способны одновременно сохранять локальную и глобальную структуру данных [5].
SNE начинается с преобразования многомерной евклидовой дистанции между точками в условные вероятности, отражающие сходство точек. Математически это выглядит следующим образом:
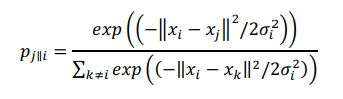 (4)
(4)Формула (4) показывает, насколько точка xj близка к точке xi при гауссовом распределении вокруг xi с заданным отклонением σ. Сигма будет различной для каждой точки. Она выбирается так, чтобы точки в областях с большей плотностью имели меньшую дисперсию. Для этого используется оценка перплексии (perplexity):
г
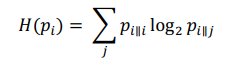 де
де - энтропия Шеннона (6)
Решение поставленной задачи
После генерации обучающей выборки следующим этапом было проверить работу алгоритма для разных значений перплексии.
#организуем цикл для 4-х значений реплексии
for (k in c(5,10,25,50)) {
res.tsne <- Rtsne(data[,-1], dims=2, perplexity=k, verbose=TRUE, max_iter=500,check_duplicates=FALSE)
colors = rainbow(length(unique(data$quality)))
plot(res.tsne$Y, t='n', main=paste('tSNE::per',k), xlab='tSNE dim 1', ylab='tSNE dim 2')
text(res.tsne$Y, labels=data$quality, col=colors[data$quality])
print('======')
}
Листинг 5
Кластеры должны окрашиваться в то количество цветов, которое совпадает с количеством уникальных значений в факторном столбце. Текущий цикл перебирает значения перплексии [5, 10, 25, 50] и графический результат представлен на рисунке 4.

Рисунок 4. Вид кластеров tSNE при различной перплексии
Если рассматривать отдельно результат кластеризации
, например для значения перплексии 50, можно увидеть, что присутствует динамика в сторону увеличения похожих на полноценные кластеры совокупностей точек, что в свою очередь может свидетельствовать о положительной возможности использовать алгоритм понижения размерности tSNE в задачах кластеризации и в искомом датасете в частности.
Для алгоритма UMAP последовательность действий, по сути, такая же, после формирования обучающей выборки вызвать функцию umap из пакета umap.
#UMAP
rows.umap <- sample(1:nrow(data), nrow(data)*0.7)
data.umap <- data[rows.umap,]
res.umap <- umap(data.umap[,-ncol(data.umap)])
colors=rainbow(10)
par(mfrow=c(1,1))
plot(res.umap$layout, t='n', main='UMAP wine Q', xlab='UMAP dim 1', ylab='UMAP dim 2',
'cex.main'=2, 'cex.lab'=1.5)
text(res.umap$layout, labels=data$quality, col=colors[data$quality])
Листинг 6

Рисунок 5. Вид кластеров UMAP
В итоге есть основания утверждать, что оба алгоритма при правильно подобранных параметрах и предварительно проверенных на корректность данных являются применимыми в задачах кластеризации.
Программный код
install.packages("readr")
install.packages("Rtsne")
install.packages("magrittr")
install.packages("data.table")
install.packages("dplyr")
install.packages("ggplot2")
install.packages("umap")
library("readr")
library("Rtsne")
library("magrittr")
library("data.table")
library("dplyr")
library("ggplot2")
library("umap")
#чтение файла
data <- read.delim('/Users/viktoriazw/Desktop/БОНЧ 2022-2023 учебный год/Подработки 2022-2023/2023/Курсовой ТОИ/Мельник/zadanie2/winequality-white.csv', sep=';')
#определить фактором столбец качества вина
data$quality <- factor(data$quality, ordered = T)
#задаем начальную фазу генератора случайных чисел - для воспроизводимости
set.seed(1)
#подготовка визуализации графиков в 2 строки по 2 графика
par(mfrow=c(2,2))
#перемешивание и определение обучающей выборки
rows.tsne <- sample(1:nrow(data), nrow(data)*0.7)
#организуем цикл для 4-х значений реплексии
for (k in c(5,10,25,50)) {
res.tsne <- Rtsne(data[,-1], dims=2, perplexity=k, verbose=TRUE, max_iter=500,check_duplicates=FALSE)
colors = rainbow(length(unique(data$quality)))
plot(res.tsne$Y, t='n', main=paste('tSNE::per',k), xlab='tSNE dim 1', ylab='tSNE dim 2')
text(res.tsne$Y, labels=data$quality, col=colors[data$quality])
print('======')
}
#UMAP
rows.umap <- sample(1:nrow(data), nrow(data)*0.7)
data.umap <- data[rows.umap,]
res.umap <- umap(data.umap[,-ncol(data.umap)])
colors=rainbow(10)
par(mfrow=c(1,1))
plot(res.umap$layout, t='n', main='UMAP wine Q', xlab='UMAP dim 1', ylab='UMAP dim 2',
'cex.main'=2, 'cex.lab'=1.5)
text(res.umap$layout, labels=data$quality, col=colors[data$quality])
Заключение
В данном разделе были получены теоретические знания и практические навыке в работе с алгоритмами понижения размерности tSNE и UMAP в задачах кластеризации.
Список использованных источников
-
Филиппов Ф.В., Технологии обработки информации, методическое пособие для курсовой работы, СПб., 2021. – 27 -
Препарируем t-SNE https://habr.com/ru/post/267041/
Контрольные вопросы
1) Как можно интерпретировать назначение и выбирать адекватное значение перплексии при использовании алгоритма t-SNE?
Перплексия может быть интерпретирована как сглаженная оценка эффективного количества «соседей» для точки xi. Она задается в качестве параметра метода t-SNE и рекомендуется использовать ее значение в интервале от 5 до 50. Сигма определяется для каждой пары xi и xj при помощи алгоритма бинарного поиска.
2) Как решается проблема скученности точек в пространстве отображения в алгоритме t-SNE?
Использование классического SNE позволяет получить неплохие результаты, но может быть связано с трудностями в оптимизации функции потерь и проблемой скученности (в оригинале – crowding problem). t-SNE если и не решает эти проблемы совсем, то существенно облегчает. Функция потерь t-SNE имеет два принципиальных отличая. Во-первых, у t-SNE симметричная форма сходства в многомерном пространстве и более простой вариант градиента. Во-вторых, вместо гауссова распределения для точек из пространства отображения используется t-распределение (Стьюдента), «тяжелые» хвосты которого облегчают оптимизацию и решают проблему скученности. [2]
3) Чем распределение Стьюдента отличается от нормального распределения?
Форма распределения Стьюдента похожа на форму нормального распределения. Отличием является то, что «хвосты» распределения Стьюдента медленнее стремятся к нулю, чем «хвосты» нормального распределения.
4) Что пытается сохранить алгоритм UMAP: глобальную структуру анализируемых данных или локальные расстояния между отдельными точками?
Алгоритм UMAP относится к группе алгоритмов, которые пытаются сохранить локальные расстояния между отдельными точками, в отличие от PCA.
Задание №3 Обработка графической информации
Визуализировать отрывок сказки К.И.Чуковского «Муха-цокотуха» с использованием технологии SVG, соответствующий номеру фрагмента. Номер своего фрагмента определяется последней цифрой номера зачетной книжки:
| Вдруг какой-то старичок Паучок Нашу Муху в уголок Поволок - Хочет бедную убить, Цокотуху погубить! "Дорогие гости, помогите! Паука-злодея зарубите! И кормила я вас, И поила я вас, Не покиньте меня В мой последний час!" |