Файл: Нахождение кратчайшего пути в графе с помощью алгоритма Дейкстры.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 101
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическая работа по теме 2.2 «Знакомство с современными российскими программными решениями на уроках информатики и во внеурочной деятельности»
Название работы: Разработка серии учебных заданий для решения задачи поиска кратчайшего пути в графе на материале геоинформационных систем
Тема занятия: Нахождение кратчайшего пути в графе с помощью алгоритма Дейкстры.
Цель проведения занятия: научиться находить кратчайшие пути в графе с помощью алгоритма Дейкстры.
После выполнения работы студент должен
знать: алгоритма Дейкстры нахождения кратчайшего пути в графе;
уметь: находить пути в графе с помощью алгоритма Дейкстры.
Материально-техническое оснащение рабочего места: инструкционные карты, конспект.
Инструктаж по технике безопасности
Содержание и порядок выполнения задания
Задание 1. Требуется найти кратчайшие расстояния от 1 -й вершины до всех остальных для графа, представленного на рисунке:
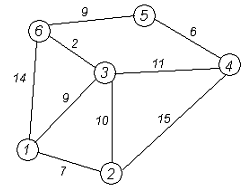
Задани2 ( по вариантам).
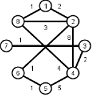
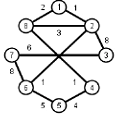
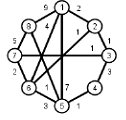
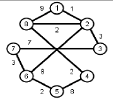
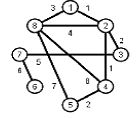
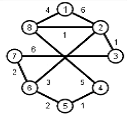
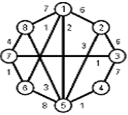
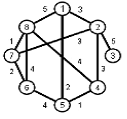
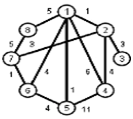
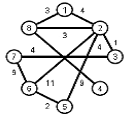
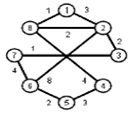
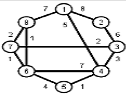
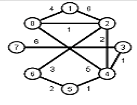
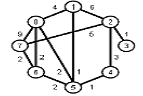
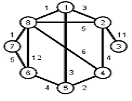
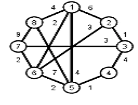
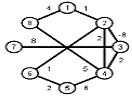
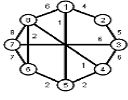
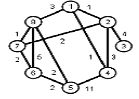
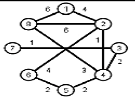
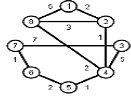
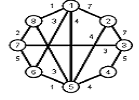
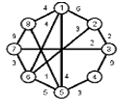
Найти кратчайшие расстояния от 1 -й вершины до всех остальных для графа, представленного на рисунке. (вес ребра брать положительный)
| |  | |  | |  | | 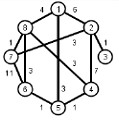 |
| | 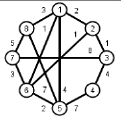 | | 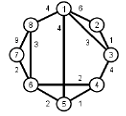 | | 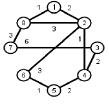 | |  |
| |  | |  | |  | |  |
| |  | |  | |  | |  |
| |  | |  | |  | |  |
| |  | |  | |  | |  |
| |  | |  | |  | |  |
| |  | |  | |  | |  |
Вопросы для самоконтроля:
-
Дайте определение понятию поиск кратчайшего пути? -
Между какими вершинами в графе алгоритм Дейкстры позволяет находить кратчайший путь? -
В чем заключается идея алгоритма поиска пути Дейкстры? -
К какому виду алгоритма поиска пути («в глубину» или «в ширину») относится алгоритм Дейкстры и почему? -
Какое условие должно выполняться для применения алгоритма Дейкстры?
Краткие сведения по теоретической части работы
Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до колледжа), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в сетях и т.п. Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Поиск кратчайшего пути ведется между двумя заданными вершинами в графе. Результатом является путь, то есть последовательность вершин и ребер, инцидентных двум соседним вершинам, и его длина. Описываемый в данном разделе алгоритм позволяет находить в графе кратчайший путь между двумя выделенными вершинами s и t при положительных длинах дуг. Этот алгоритм, предложенный в 1959 г. Дейкстрой, считается одним из наиболее эффективных алгоритмов решения задачи. Алгоритм работает только для графов без рёбер отрицательного веса. Любая задача, требующая нахождения оптимальных маршрутов может быть выполнена с помощью алгоритма Дейкстры. Это касается и сетей, и транспортных потоков, и обработка графов. Очень часто используется не сам алгоритм в чистом виде, а его модификация.
Методические рекомендации по выполнению и оформлению
Порядок выполнения работы:
1. Изучить инструкцию к практической работе.
2. Выполнить задание.
3. Оформить отчет.
Содержание отчета о занятии:
1. Тема.
2. Цель.
4. Практическое задание.
5. Ответ на 1 контрольный вопрос (по указанию преподавателя).