Добавлен: 05.12.2023
Просмотров: 84
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
муниципальное бюджетное общеобразовательное учреждение города Ульяновска "Губернаторский лицей № 101 имени Народного учителя Российской Федерации Ю.И. Латышева" при ФГБОУ ВО "УлГПУ им. И.Н. Ульянова"
Проект на тему:
«Другие способы умножения»
Выполнил: ученик 6 Класса Т1 Лимасов Егор
Руководитель: учитель математики высшей квалификационной категории Нуруллин Н.И.
Ульяновск, 2023
Содержание
Введение
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
В нашем современном обществе, когда у каждого есть телефон с калькулятором, мы всё чаще и чаще используем его, забывая, как можно без всякой техники легко и быстро выполнить умножение больших чисел.
Постоянное применение современной вычислительной техники приводит к тому, что ученики затрудняются производить какие-либо расчеты, не имея в своем распоряжении таблиц или калькулятора. Знание упрощенных приемов вычислений дает возможность не только быстро производить простые расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки. Кроме того, освоение вычислительных навыков развивает память, повышает уровень математической культуры мышления, помогает полноценно усваивать предметы физико-математического направления.
Целью данной работы является исследование различных способов умножения чисел и повышение интереса к математике
Объект исследования: Способы письменного умножения чисел.
Предмет исследования: Процесс выполнения умножения чисел с помощью ручки и бумаги.
Гипотеза: Можно предположить, что существуют различные способы выполнения умножения чисел и среди них найдется способ, альтернативный классическому, изучаемому в школе.
Для достижения данной цели необходимо решить следующие поставленные задачи:
-
Изучить литературу по выбранной теме, определить наиболее интересные способы выполнения умножения многозначных чисел. -
Проанализировать полученные результаты и систематизировать их. -
Провести практическую работу по выполнению умножения чисел различными способами.
Актуальность проблемы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес к математике и содействует развитию математических способностей.
Новизна проекта
Новизна данного проекта заключается в получении автором новых способов умножения чисел и их систематизация.
Практическая значимость
Выполнение умножения несколькими способами позволяет учащимся сформировать представление о свойствах этого математического действия, позволяет в каждом конкретном случае решить задачу рационально, а также проверить полученный результат.
Работа состоит из введения, двух глав, заключения и приложения1(продукта проектной деятельности)
В первой главе рассматриваются разные способы умножения на примере конкретных примеров. Вторая глава содержит анализ, раскрывающий скорость выполнения вычислений каждым способом, что позволяет сделать вывод о рациональности использования того или иного способа.
-
Из истории умножения
Умножение - это особый случай сложения нескольких одинаковых чисел. В далекие времена люди учились умножать уже при счете предметов. Так, считая по порядку числа 17, 18, 19, 20, они должны были представлять 20 не только как 10+10, но и как два десятка, 30 - как три десятка,- и так далее. Умножать люди начали значительно позже, чем складывать. Египтяне выполняли умножение посредством повторного сложения или последовательного удвоения. В Вавилоне при умножении чисел пользовались специальными таблицами умножения - «предками» современных. В Древней Индии применяли способ умножения чисел, тоже довольно близкий к современному. Индийцы производили умножение чисел, начиная с высших разрядов. При этом они стирали те цифры, которые при последующих действиях надо было заменять, так как к ним прибавляли число, ныне запоминаемое нами при умножении. Таким образом, математики Индии сразу записывали произведение, выполняя промежуточные вычисления на песке или в уме. Индийский прием умножения перешел к арабам. Но
арабы не стирали цифры, а перечеркивали их и надписывали новую цифру над перечеркнутой. В Европе продолжительное время произведение называли сумма умножения.
В XVII веке некоторые из математиков стали обозначать умножение косым крестиком, а иные употребляли для этого точку. Только в конце XVIII века большинство математиков стали употреблять в качестве знака умножения точку, но допускали и употребление косого креста. Знаки умножения и знак равенства стали общепризнанными благодаря авторитету знаменитого немецкого математика Готфрида Вильгельма Лейбница (1646 -1716).
В современной школе умение быстро умножать многозначные числа, которое школьники получают к концу начальной школы, постепенно без постоянных систематических тренировок в среднем звене, теряет своё прямое назначение. Многие школьники не скрывают, что пользуются всё чаще при вычислениях калькулятором. И лишь по требованию учителя, показать развёрнутый полный ответ, прописывают решения примеров столбиками. А может быть существуют другие, более лёгкие способы счёта, о которых известно мало? Возможно, не во всех странах используют столбик?
Проанализировав литературу по выбранной теме, выделим следующие методы:
1. Японский или китайский способ умножения
Допустим, нам надо умножить 52 на 25 (рис.1). Для этого нужно начертить 14 линий. Эти линии обозначают число 52 (5 горизонтальных линий, отступ, 2 горизонтальные линии) и число 25 (2 вертикальные линии, отступ, 5 вертикальных линий).
Теперь нужно сосчитать пересечения линий на всех четырех концах следующим образом: (пересечения на рисунке указаны точками)
Количество пересечений:
Верхний левый край: 10
Нижний левый край: 4
Верхний правый: 25
Нижний правый: 10
1) Пересечения в верхнем левом крае (10) – первое число ответа
2) Сумма пересечений нижнего левого и верхнего правого краев (4+25) – второе число ответа
3) Пересечения в нижнем правом крае (10) – третье число ответа.
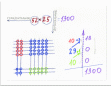
Рис. 1. «Японский или китайский способ умножения»
Получается: 10; 29; 10.
Так как два последних числа – двузначные и мы не можем их записать, то записываем только единицы, а десятки прибавляем к предыдущему разряду.
Ответ: 1300
2. Итальянский способ умножения «Сеткой»
В Италии, а также во многих странах Востока, этот способ приобрел большую известность. Использование приема: умножим также 52 на 25. будем действовать согласно алгоритму:
1. Вычерчиваем квадратную сетку и пишем одно из чисел над колонками, а второе по высоте.
2. Умножаем число каждого ряда последовательно на числа каждой колонки.
5∙2 = 10. Записываем 1 и 0
5∙5 = 25. Записываем 2 и 5
3.Если при умножении получается однозначное число, записываем вверху 0, а внизу это число. (Как у нас в примере при умножении 2 на 2 получилось 4 . Вверху мы записали 0, а внизу 4)
Заполняем всю сетку и складываем числа, следуя диагональным полосам (рис.2). Начинаем складывать справа налево снизу. Если сумма одной диагонали содержит десятки, то прибавляем их к единицам следующей диагонали.
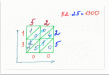
Рисунок 2 «Итальянский способ умножения»
Ответ: 1300.
3. Индийский способ умножения
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких-нибудь разрядов, определяется нулями, приписываемыми к цифрам.
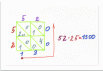
Рисунок 3. «Индийский способ умножения»
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 52 на 25 (рис.3).
-
Древнерусский способ умножения
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа
, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.

Рисунок 4. «Древнерусский способ»
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2∙3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 (рис.4). Так можно вычислять произведение любых однозначных чисел, больше 5.
5. Русский крестьянский способ
В России среди крестьян был распространен способ, который не требовал знания всей таблицы умножения. Здесь необходимо лишь умение умножать и делить числа на 2.
Напишем одно число слева, а другое справа на одной строке. Левое число будем делить на 2, а правое – умножать на 2 и результаты записывать в столбик (рис.5)
Если при делении возник остаток, то его отбрасывают. Умножение и деление на 2 продолжают до тех пор, пока слева не останется 1. Затем вычеркиваем те строчки из столбика, в которых слева стоят четные числа. Теперь сложим оставшиеся числа в правом столбце.
.
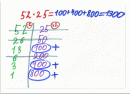
Рисунок 5. «Русский крестьянский способ»
6.«Умножение крестиком» из Древней Греции
Древние греки и индусы в старину называли прием перекрестного умножения «способом молнии» или «умножение крестиком».

Рисунок 6. Древнегреческий способ»
Пример: 52 х 25 = 1300
Последовательно производим следующие действия:
1. 2 х 5 = 10 – ноль это последняя цифра результата, 1 запоминаем и прибавляем к следующему полученному результату.
2. 2 х 2 = 4; ,5 х 5 = 25; 4 + 25 = 29 ; 29 + 1 = 30 -
0 – предпоследняя цифра в ответе, 3 запоминаем и прибавляем к следующему полученному результату (рис.6).
3. 5 х 2 = 10, 10 + 3 = 13 – это первые цифры в ответе.
Ответ: 1300.
Этим способом удобно пользоваться и в настоящее время.
7. Египетское умножение
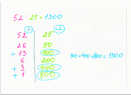
Рисунок 7. «Египтеский способ»
В мире существуют разные способы умножения, порой непривычные для нас, совсем непохожие на наши правила умножения. К примеру, в Древнем Египте не было таблиц умножения. Но они умножали разложением чисел в двоичный ряд - так называемый «компьютерный» способ.
Например, нужно умножить 52 на 25.
1. Записываем 52 и 25.
2. Теперь левое число делим на 2, а правое умножаем на 2.
3. Так продолжается, пока в левой колонке не появится 1.