Файл: Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.12.2023
Просмотров: 26
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Контрольная работа
Последнее две цифры пароля 03
Задача1
Задача посвящена анализу переходного процесса в цепи первого порядка, содержащей резисторы, конденсатор или индуктивность. В момент времени
t=0 происходит переключение ключа К, в результате чего в цепи возникает переходной процесс.
-
Перерисуйте схему цепи (таблица 2) для Вашего варианта – последним двум цифрам пароля (таблица 1). -
Выпишите числовые данные для Вашего варианта – последним двум цифрам пароля (таблица 3). -
Рассчитайте все токи и напряжение на С или L в три момента времени t: 0-,0+,∞ -
Рассчитайте классическим методом переходный процесс в видеuL(t),i1(t), i2(t), i3(t)в схемах 1 – 5, i1(t), i2(t), i3(t), uС(t)в схемах 6 – 10. Проверьте правильность расчетов, выполненных в п. 4, путем сопоставления их с результатами расчетов в п. 3. -
Постройте графики переходных токов и напряжения, рассчитанных в п. 4. Определите длительность переходного процесса, соответствующую переходу цепи в установившееся состояние с погрешностью 5%. -
Рассчитайте ток i2(t) операторным методом.
Таблица 1
| Варианты (две последние цифры пароля) | Номер схемы или задания |
| 00 10 20 30 40 50 60 70 80 90 01 11 21 31 41 51 61 71 81 91 02 12 22 32 42 52 62 72 82 92 03 13 23 33 43 53 63 73 83 93 04 14 24 34 44 54 64 74 84 94 05 15 25 35 45 55 65 75 85 95 06 16 26 36 46 56 66 76 86 96 07 17 27 37 47 57 67 77 87 97 08 18 28 38 48 58 68 78 88 98 09 19 29 39 49 59 69 79 89 99 | 1 2 3 4 5 6 7 8 9 10 |
Таблица 2
| номер схемы | Задание | номер схемы | Задание |
| 1 | 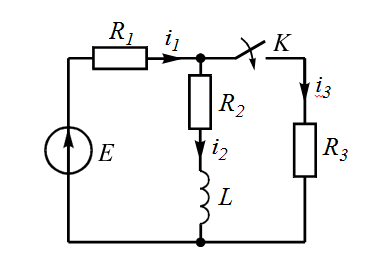 | 6 | 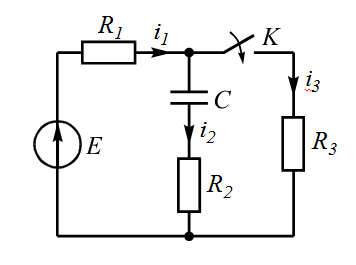 |
| 2 | 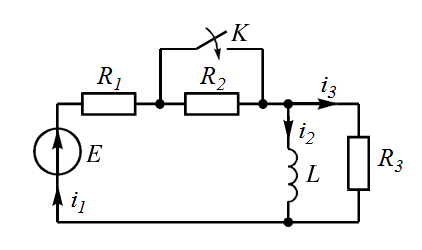 | 7 | 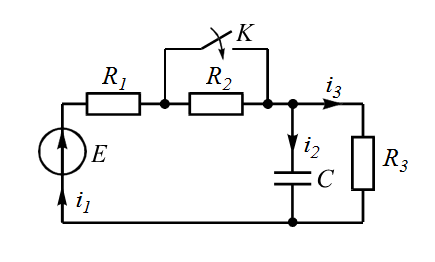 |
| 3 | 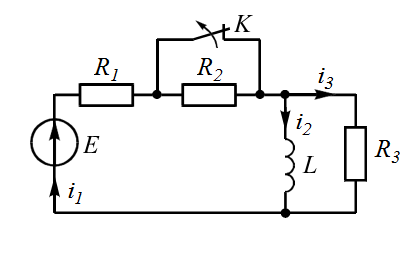 | 8 | 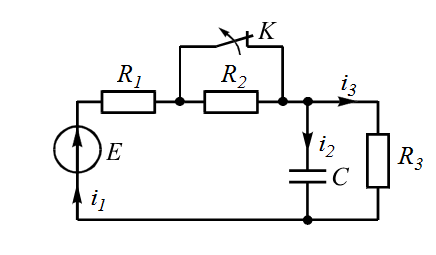 |
| 4 | 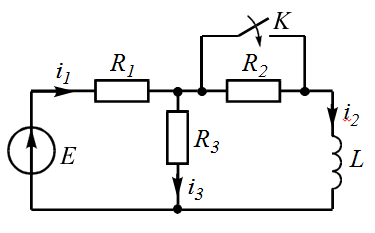 | 9 | 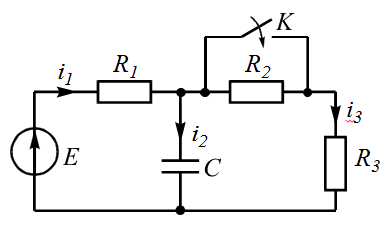 |
| 5 | 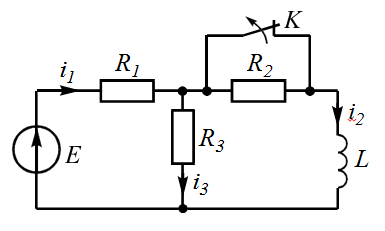 | 10 | 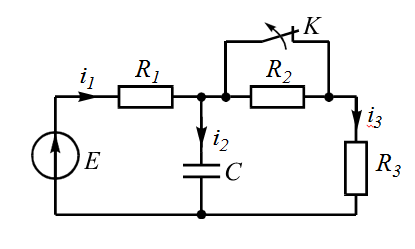 |
Таблица 3
| Варианты (две последние цифры пароля) | С, нФ или L, мГн | R1 , кОм | R2 , кОм | R3 , кОм | Е, В |
| От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 | 20 10 10 15 15 15 20 20 15 10 | 2 1 1 1 2 1 2 2 1 0,5 | 2 1 2 1 2 2 1 1 0,5 1 | 2 1 2 2 1 1 2 1 0,5 1 | 10 5 12 12 10 10 12 12 5 5 |
Задача 2
Задача посвящена временному и частотному (спектральному) методам расчета реакции цепей на сигналы произвольной формы. В качестве такого сигнала используется импульс прямоугольной формы. Электрические схемы цепей содержат емкости С или индуктивности L, а также сопротивления R. Для всех вариантов R2=3R.
В схемах, где имеется сопротивление R3 , его величина R3 0,2R1 . Во всех схемах входным напряжением u1tявляется прямоугольный импульс длительностью tи и амплитудой U1.
-
Перерисуйте схему Вашего варианта (см. табл. 1 и табл. 5). Выпишите исходные данные Вашего варианта (таблица 4).
Таблица 4
| Варианты (две последние цифры пароля) | С, пФ или L, мкГн | R1 , кОм | tи , нс | U1 , В |
| От 00 до 09 От 10 до 19 От 20 до 29 От 30 до 39 От 40 до 49 От 50 до 59 От 60 до 69 От 70 до 79 От 80 до 89 От 90 до 99 | 20 25 30 20 25 30 20 25 30 25 | 1 1 1 2 2 2 3 3 3 2,5 | 30 35 40 35 40 45 35 40 45 35 | 3 4 5 6 7 3 4 5 6 7 |
Временной метод расчета
-
Рассчитайте переходную g2(t) и импульсную h2(t) характеристики цепи по напряжению классическим или операторным методами (по выбору). -
Рассчитайте реакцию цепи в виде выходного напряжения, используя:
- интеграл Дюамеля;
- интеграл наложения
4. Постройте временные диаграммы входного и выходного напряжений в одинаковом масштабе
Частотный метод расчета
5. Рассчитайте комплексные спектральные плотности входного U1(jω) и выходного U2(jω) сигналов.
6. Запишите выражение комплексной передаточной функции цепи
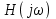 .
.7. Рассчитайте и постройте графики модулей
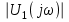 ,
, 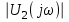 и модуля комплексной передаточной функции цепи
и модуля комплексной передаточной функции цепи 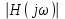 , как функции от частоты f в диапазоне частот 0 – 3/tи.
, как функции от частоты f в диапазоне частот 0 – 3/tи.Таблица 5
| номер схемы | Исходные схемы | номер схемы | Исходные схемы |
| 1 | 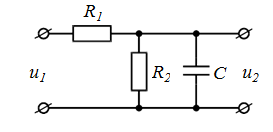 | 6 | 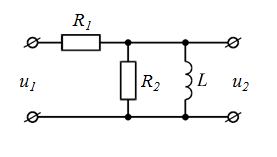 |
| 2 | 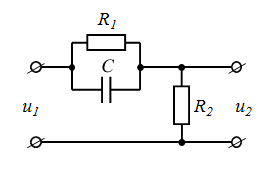 | 7 | 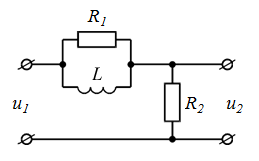 |
| 3 | 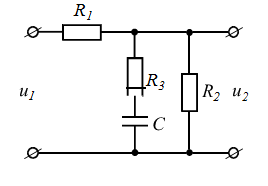 | 8 | 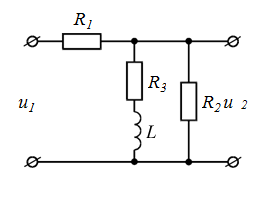 |
| 4 | 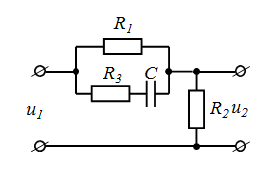 | 9 | 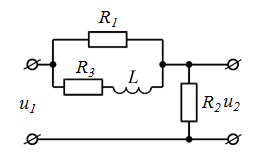 |
| 5 | 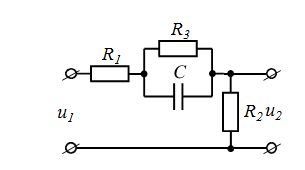 | 10 | 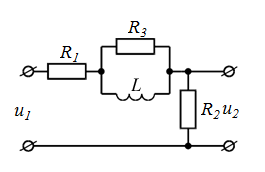 |