Файл: Методические указания к лабораторным работам Составитель Сухарев В. В. Москва ргу им. А. Н. Косыгина 2018 удк 003. 023.docx

Решение системы линейных уравнений

Пусть есть система линейных уравнений (рис. 20).



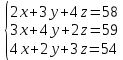
Рисунок 20

Решим эту систему с использованием типовых возможностей Microsoft Excel двумя способами.

Первый способ – метод обратной матрицы

Запишем систему уравнений в Excel

Матрица коэффициентов					Свободные члены
2	3	4		58
3	4	2		59
4	2	3		54

Рисунок 21

Решение системы линейных уравнений возможно только в том случае, если определитель матрицы не равен нулю. Поэтому первоначально рассчитаем определитель матрицы.

Для этого используем функцию МОПРЕД( ).

В свободной ячейке записывается функция МОПРЕД( ), в качестве параметра функции передается диапазон ячеек матрицы коэффициентов (рис. 21).

В нашем случае определитель матрицы равен -27, поэтому решение системы уравнений возможно.

Далее для решения необходимо определить обратную матрицу. Для это используется функция МОБР( ). Чтобы вычислить обратную матрицу, нужно

- выделить область ячеек, в которую будет помещен результат. Выделенная область должна совпадать по размерам с исходной матрицей;

- в строке формул записать функцию МОБР(диапазон), в качестве аргумента функции передается диапазон ячеек с исходной матрицей;

- нажать CTRL+SHIFT+ENTER

Чтобы решить систему уравнений, нужно умножить обратную матрицу на столбец свободных членов.

Для перемножения используется функция МУМНОЖ( ). Функция имеет два аргумента. В качестве первого передается диапазон ячеек с обратной матрицей, в качестве второго – диапазон ячеек со свободными членами.

---

Порядок осуществления вычислений:

- выделить диапазон ячеек для ответов (в нашем случае – три вертикальные ячейки);

- в строке формул записать функцию МУМНОЖ(Матрица;Столбец)

- нажать CTRL+SHIFT+ENTER

Внимание! Если при вычислении обратной матрицы и умножения нажать ENTER – вычисления будут произведены только для одной ячейки!

Если все сделано правильно , то в столбец ответов будут подставлены результаты 5,8,6. Соответственно, X = 5, Y = 8, Z = 6.

Общий вид задания и решения приведен на рисунке 22



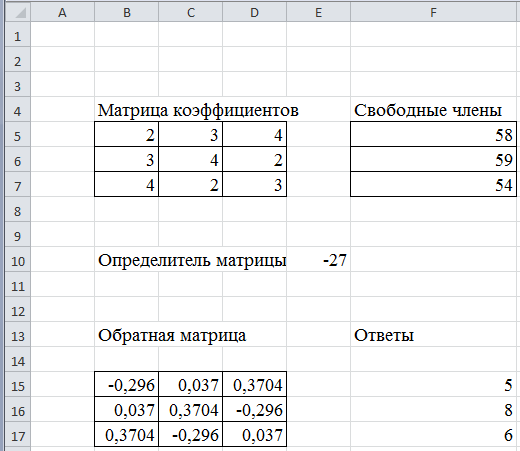
Рисунок 22

Использованные функции с примерами записи для контрольного примера

Вычисление определителя: = МОПРЕД(B5:D7)

Вычисление обратной матрицы: =МОБР(B5:D7)

Умножение матрицы на столбец: =МУМНОЖ(B15:D17;F5:F7)

Второй способ решения системы линейных уравнений – использование метода Крамера.

Для того, чтобы проверить, не является ли матрица вырожденной и что указанная система уравнений имеет только одно решение, найдем определитель матрицы.

Так как исходные данные у нас те же, то определитель матрицы у нас уже рассчитан.

Далее, согласно методу Крамера, столбцы матрицы поочередно меняются на столбец свободных членов и для каждой полученной матрицы рассчитывается определитель. Вычисления приведены на рисунках 23-25.

58 3 4 59 4 2 54 2 3 определитель 1 -135

2 58 4 3 59 2 4 54 3 определитель 2 -216

2 3 58 3 4 59 4 2 54 определитель 3 -162

---

Рисунки 23- 25

Решения уравнений рассчитываются как отношения определителей полученных матриц к определителю исходной матрицы

В нашем случае получается

X = - 135 / (-27) = 5

Y = - 216 / (-27) = 8

Z = - 162 / (-27) = 6

---

Абсолютная и относительная адресация

При записи формул может быть использовано два вида адресации ячеек

- абсолютная

- относительная.

При использовании относительной адресации в формулу подставляются не значения указанных ячеек, а их местоположение относительно той ячейки, в которой указана формула. Использование относительной адресации позволяет копировать формулы в таблице без ручного заполнения (корректировки) формул в каждой ячейке.

При копировании формулы с использованием относительной адресации вместо указанных в первичной формуле адресов ячеек автоматически подставляются адреса ячеек, полученные путем соответствующего смещения для скопированной ячейки.

Наглядно относительная адресация видна при использовании стиля ссылок R1C1.

Рассмотрим таблицу на рисунке 4

	A	B	C	D
1	3	4		7
2	5	6		11

Рисунок 4

В ячейке D1 записана формула сложения двух ячеек: = A1 + B1.

При копировании в ячейку D2 формула примет вид: = A2 + B2

Если переключить стиль ссылок на R1C1, формула примет вид: = RC[-3] + RC[-2]. При копировании формулы в нашем случае вид формулы останется без изменений. В самом деле, в полученной формуле запись R означает, что идет обращение к ячейке в той же строке, поэтому смещение отсутствует. А запись С[-3] означает, что осуществляется смещение на три столбца влево.

При использовании абсолютной адресации в формулу подставляется не ссылка на значение относительно текущей ячейки, а непосредственно значение из указанной ячейки.

При использовании абсолютной адресации таблица, представленная на рис. 4, примет вид, указанный на рисунке 5.

	A	B	C	D
1	3	4		7
2	5	6		7

---

Рисунок 5

Для относительной адресации формула из ячейки D4 будет иметь вид: = $A$1+$B$1, а для абсолютной адресации = R1C1+R1C2. При копировании во вторую строку формулы не изменятся.

Строго говоря, фиксирование столбца в нашем случае является избыточным, символ «$» указывает, что осуществляется фиксация только того измерения, которое указано непосредственно за ним. В нашем примере изменение столбца не осуществляется и формула может иметь вид : = A$1+B$1. Результат при этом не изменится.

При изменении стиля ссылок в настройках система автоматически переведет все формулы в новый выбранный стиль ссылок.

Поиск в подмножестве

Поиск в подмножестве целесообразно использовать в том случае если в таблице несколько раз используются значения, относящиеся к одному и тому же показателю. При изменении значений или добавлении нового значения приходится корректировать и все показатели, относящиеся к добавляемому (изменяемому) значению. Например, при составлении отчета о продажах товара по дням среди показателей за каждый день продаж фигурируют одни и те же позиции, с одной и той же ценой и одинаковым наименованием. Для одной и той же позиции оператор должен указать

- артикул (для однозначной идентификации товара)

- наименование товара

- цена товара

Автоподстановка значений наименования и цен значительно сократит время работы оператора, а также существенно снизит вероятность ошибок при заполнении значений реквизитов.

Рассмотрим таблицу на рис. 6

	A	B	C	D	E	F
1	Отчет о продажах
2	Дата	Артикул	Наименование	Цена	Количество	Сумма
3	01.10.2017	1234	Кофта	100	3	300
4	01.10.2017	2222	Жилет	200	2	400
5	01.10.2017	3333	Брюки	300	5	1500
6	02.10.2017	1234	Кофта	100	2	200
7	02.10.2017	2222	Жилет	200	3	600
8	02.10.2017	3333	Брюки	300	6	1800
9	02.10.2017	4444	Свитер	700	1	700

---