Файл: Проектирование многоэтажного промышленного здания с неполным каркасом.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.12.2023
Просмотров: 293
Скачиваний: 9
СОДЕРЖАНИЕ
1.Компоновка конструктивной схемы здания
Схема расположения основных конструктивных элементов
2. Расчет и конструирование ребристой плиты перекрытия
2.1. Сбор нагрузок на 1 м2перекрытия
2.3. Назначение размеров железобетонного ригеля, железобетонной плиты перекрытия.
2.4. Характеристики прочности бетона и арматуры
3.1 Расчет прочности плиты по сечению нормальному продольной оси
3.2 Расчет полки плиты на местный изгиб
3.4 Расчет прочности плиты по сечению наклонному к продольной оси
4.Расчет ребристой плиты перекрытия по II гр. предельных состояний
4.1 Определение геометрических характеристик приведенного сечения
5.3Характеристика прочности бетона и арматуры
5.4 Расчет прочности ригеля по сечению нормальному продольной оси
5.5 Расчет прочности ригеля по сечению наклонному к продольной оси
5.5 Построение эпюры материалов
| |  | |
| |  | |
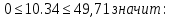
| | 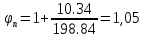 | |
Проверим первое условие:
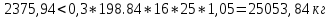
Условие выполняется.
Второе условие. Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил производят из условия:
| | 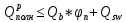 |
| | 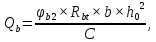 | |
где:
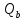 – поперечная сила, воспринимаемая бетоном в наклонном сечении, величина принимается не более
– поперечная сила, воспринимаемая бетоном в наклонном сечении, величина принимается не более 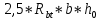 и не менее
и не менее 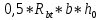 ;
;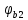 – коэффициент, принимаемый равным 1,5;
– коэффициент, принимаемый равным 1,5;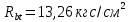 – расчетное сопротивление бетона на осевое растяжение;
– расчетное сопротивление бетона на осевое растяжение;С – длина проекции наиболее опасного наклонного сечения, принимается не менее
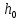 и не более
и не более 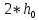 .
.| | 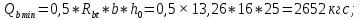 | |
| | 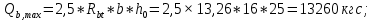 | |
| | 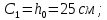 | |
| | 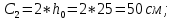 | |
| | 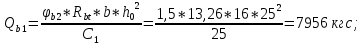 | |
| | 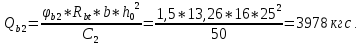 | |
| | 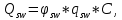 | |
где:
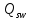 – поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении;
– поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении;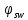 – коэффициент, принимаемый равным 0,75;
– коэффициент, принимаемый равным 0,75;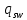 – усилие в поперечной арматуре на единицу длины элемента, при условии что:
– усилие в поперечной арматуре на единицу длины элемента, при условии что: 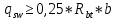 ;
;| | 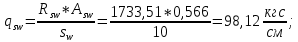 | |
где: где
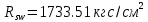 – расчетное сопротивление поперечной арматуры растяжению;
– расчетное сопротивление поперечной арматуры растяжению;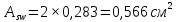 – площадь поперечных стержней, равная
– площадь поперечных стержней, равная 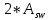 , т.к. в поперечном сечении расположены 2 плоских каркаса;
, т.к. в поперечном сечении расположены 2 плоских каркаса;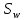 – шаг поперечных стержней, равный 10 см.
– шаг поперечных стержней, равный 10 см.Проверим условие в поперечной арматуре:
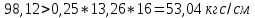
Условие выполняется.
Определим поперечную силу, воспринимаемую поперечной арматурой:
| | 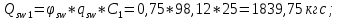 | |
| | 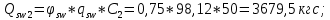 | |
Проверим второе условие:
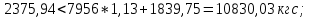
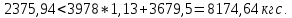
Условие выполняется.
Третье условие. Расчет железобетонных элементов по наклонным сечениям на действие моментов производят из условия:
| | 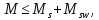 | |
где:
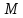 – момент в наклонном сечении с длинной проекции С на продольную ось элемента;
– момент в наклонном сечении с длинной проекции С на продольную ось элемента;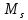 – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
– момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения; 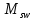 – момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения.
– момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения.| |
| |
| | 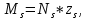 | |
где:
 – момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
– момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения; 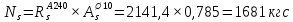 – усилие в продольной растянутой арматуре;
– усилие в продольной растянутой арматуре;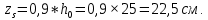
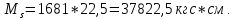
| | 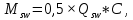 | |
где:
 – момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения;
– момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения; – усилие в поперечной арматуре.
– усилие в поперечной арматуре.| | 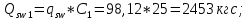 | |
| | 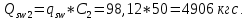 | |
| | 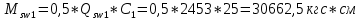 | |
| | 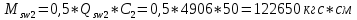 | |
Проверим третье условие:
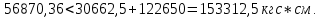
Условие выполняется.
4.Расчет ребристой плиты перекрытия по II гр. предельных состояний
4.1 Определение геометрических характеристик приведенного сечения
Для расчета предварительно-напряженной плиты по второй группе предельных состояний, необходимо определить геометрические характеристики приведенного сечения. Сложное расчетное сечение для упрощения расчета необходимо разбить на простые фигуры (например, прямоугольники), а затем ввести вспомогательную систему координат «y-x0».
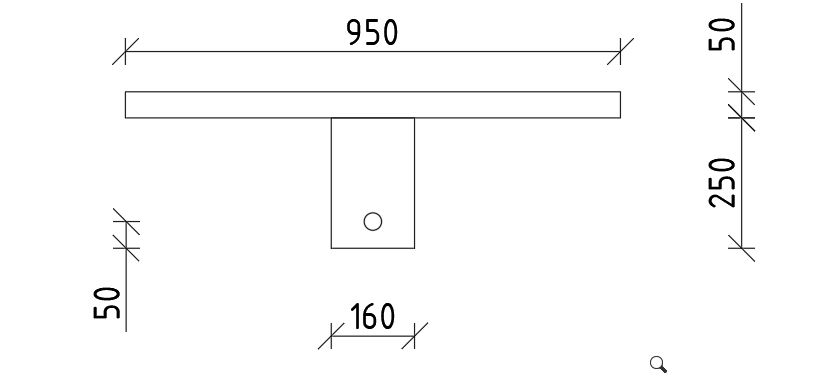
Рисунок 12 – Приведенное поперечное сечение плиты перекрытия
1 – первая фигура; 2 – вторая фигура; 3 – третья фигура (ПН арматура)
Бетон и арматура, хотя и работают совместно, но имеют разные модули упругости: при одинаковых деформациях в них возникают разные напряжения, поэтому сечение арматуры приводится к одному материалу (обычно к бетону) через коэффициент приведения, который равен:
| | 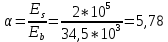 | |
Площадь приведенного сечения:
| | 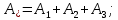 | |
| | 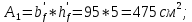 | |
| | 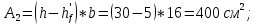 | |
| | 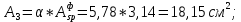 | |