Файл: Отчет по курсовой работе по предмету Сиаод Вариант х студент группы Москва 2023.docx

Скачать файл (0,48Мб)

Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 11.12.2023

Просмотров: 180

Скачиваний: 6

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

СОДЕРЖАНИЕ

Федеральное агентство связи

Ордена Трудового Красного Знамени

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра Математической Кибернетики и Информационных Технологий

Отчет по курсовой работе

по предмету «СиАОД»

Вариант Х

Выполнил: студент группы:

Руководитель:

Москва 2023

Задание №1

Цель работы
Реализовать заданный метод сортировки строк числовой матрицы в соответствии с индивидуальным заданием. Для всех вариантов добавить реализацию быстрой сортировки (quicksort). Оценить время работы каждого алгоритма сортировки и сравнить его со временем стандартной функции сортировки, используемой в выбранном языке программирования.
Вариант 6

Пирамидальная сортировка (Heap Sort).
Ход работы

В соответствии с заданием реализован алгоритм пирамидальной сортировки на языке Python:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

def heapify(arr, n, i):

root = i

left = 2 * i + 1

right = 2 * i + 2
if left < n and arr[i] < arr[left]:

root = left

if right < n and arr[root] < arr[right]:

root = right

if root != i:

arr[i],arr[root] = arr[root],arr[i]
heapify(arr, n, root)
def heap_sort(arr, n):

n = len(arr)

for i in range(n, -1, -1):

heapify(arr, n, i)

for i in range(n-1, 0, -1):

arr[i], arr[0] = arr[0], arr[i]

heapify(arr, i, 0)

Также реализован алгоритм быстрой сортировки:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

def partition(items, low, high):

pivot = items[(low + high) // 2]

i = low - 1

j = high + 1

while True:

i += 1

while items[i] < pivot:

i += 1

j -= 1

while items[j] > pivot:

j -= 1

if i >= j:

return j

items[i], items[j] = items[j], items[i]
def quick_sort(arr):
def _quick_sort(items, low, high):

if low < high:

split_index = partition(items, low, high)

_quick_sort(items, low, split_index)

_quick_sort(items, split_index + 1, high)
_quick_sort(arr, 0, len(arr) - 1)

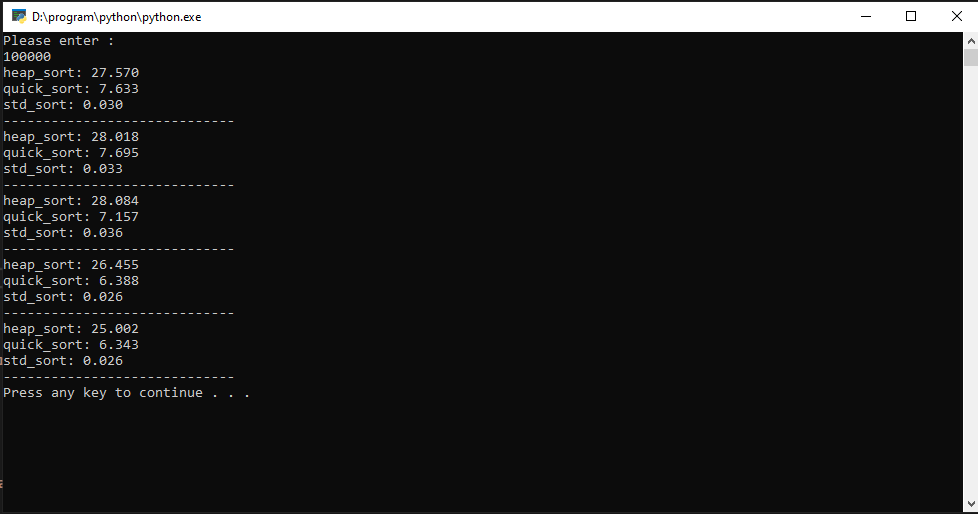
равнение времени выполнения алгоритмов, для массива размером 100000:

n	Пирамидальная, с	Быстрая, с	Стандартная, с
1	27.57	7.633	0.03
2	28.018	7.695	0.033
3	28.084	7.157	0.036
4	26.433	6.388	0.026
5	25.002	6.343	0.026

Среднее время выполнения:

Пирамидальная: 27,02 с;

Быстрая: 7,04 с;

Стандартная: 0,03с.

Наилучший результат показала стандартная сортировка. У пирамидальной самое большое среднее время.

С

равним время выполнения алгоритмов, для массива размером 1000000:

n	Пирамидальная, с	Быстрая, с	Стандартная, с
1	297,633	69,245	0,528
2	288,505	67,819	0,491
3	291,347	68,810	0,496
4	292,617	68,38	0,502
5	290,489	68,761	0,495

Среднее время выполнения:

Пирамидальная: 292,1 с;

Быстрая: 68,6 с;

Стандартная: 0,5 с.

Код программы:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

67

68

69

70

71

72

73

74

75

76

77

78

79

80

81

82

83

84

85

86

87

88

89

90

91

92

93

94

95

96

97

98

99

100

101

import random

import time
def heapify(nums, heap_size, root_index):

# Индекс наибольшего элемента считаем корневым индексом

largest = root_index

left_child = (2 * root_index) + 1

right_child = (2 * root_index) + 2
# Если левый потомок корня — допустимый индекс, а элемент больше,

# чем текущий наибольший, обновляем наибольший элемент

if left_child < heap_size and nums[left_child] > nums[largest]:

largest = left_child
# То же самое для правого потомка корня

if right_child < heap_size and nums[right_child] > nums[largest]:

largest = right_child
# Если наибольший элемент больше не корневой, они меняются местами

if largest != root_index:

nums[root_index], nums[largest] = nums[largest], nums[root_index]

# Heapify the new root element to ensure it's the largest

heapify(nums, heap_size, largest)
def heap_sort(nums):

n = len(nums)
# Создаём Max Heap из списка

# Второй аргумент означает остановку алгоритма перед элементом -1, т.е.

# перед первым элементом списка

# 3-й аргумент означает повторный проход по списку в обратном направлении,

# уменьшая счётчик i на 1

for i in range(n, -1, -1):

heapify(nums, n, i)
# Перемещаем корень Max Heap в конец списка

for i in range(n - 1, 0, -1):

nums[i], nums[0] = nums[0], nums[i]

heapify(nums, i, 0)

def partition(items, low, high):

pivot = items[(low + high) // 2]

i = low - 1

j = high + 1

while True:

i += 1

while items[i] < pivot:

i += 1

j -= 1

while items[j] > pivot:

j -= 1

if i >= j:

return j

items[i], items[j] = items[j], items[i]
def quick_sort(arr):
def _quick_sort(items, low, high):

if low < high:

split_index = partition(items, low, high)

_quick_sort(items, low, split_index)

_quick_sort(items, split_index + 1, high)
_quick_sort(arr, 0, len(arr) - 1)

def std_sort(arr):
arr2 = sorted(arr)
def main():

print('Please enter :')

n = int(input())

for _ in range(5):

arr = list(range(1, n))

random.shuffle(arr)
arr_copy = arr.copy()

start = time.perf_counter()

heap_sort(arr_copy)

end = time.perf_counter()

print(f"heap_sort: {end-start:.3f}")

arr_copy = arr.copy()

start = time.perf_counter()

quick_sort(arr_copy)

end = time.perf_counter()

print(f"quick_sort: {end-start:.3f}")

start = time.perf_counter()

std_sort(arr)

end = time.perf_counter()

print(f"std_sort: {end-start:.3f}")

print('-----------------------------')

if __name__ == '__main__':

main()

Вывод

Увеличение размера массива, не привело к новым выводам, стандартная сортировка Python, по-прежнему самая быстрая, по сколько она основана на алгоритме TimSort (сортировка вставками и слиянием), а пирамидальная самая медленная.

Задание №2

Цель работы
Реализовать заданный метод поиска в соответствии с индивидуальным заданием. Организовать генерацию начального набора случайных данных. Для всех вариантов добавить реализацию добавления, поиска и удаления элементов. Оценить время работы каждого алгоритма поиска и сравнить его со временем работы стандартной функции поиска, используемой в выбранном языке программирования.
Вариант 6

Интерполяционный метод поиска.

Хэширование методом цепочек.
Ход работы

Часть 1.

Для интерполяционного метода поиска массив будет отсортирован по возрастанию. В качестве стандартного метода Python, выбрана функция count(), которая считает количество вхождений элемента, если она вернет 0, значит такого элемента нет в списке. Для подсчета времени используется функция perf_counter(), модуля time, т.к. поиск осуществляется слишком быстро и функция time() не может корректно посчитать время.

Ниже приведен код программы:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

24

25

26

27

28

29

30

31

32

33

34

35

36

37

38

39

40

41

42

43

44

45

46

47

48

49

50

51

52

53

54

55

56

57

58

59

60

61

62

63

64

65

66

import time
def add(data):

print('Enter value for Insert')

n = int(input())

if data.count(n) > 0:

print('The number is already in the list')

else:

data.append(n)

print('Value', n, 'added!')
def delete(data):

print('Enter a number to Delete:')

n = int(input())

if data.count(n) <= 0:

print('This value is not on the list')

else:

data.remove(n)

print('Value', n, 'deleted!')
def InterpolationSearch(data, n):

low = 0

high = (len(data) - 1)

while low <= high and n >= data[low] and n <= data[high]:

index = low + int(((float(high - low) / ( data[high] - data[low])) * ( n - data[low])))

if data[index] == n:

return 1

elif data[index] < n:

low = index + 1;

else:

high = index - 1;

return print('Not found!')
def stdSearch(data, n):

if data.count(n) > 0:

return 1

else:

return 0
def main():

array_for_test = 50000 # 50 000,500 000, 5 000 000

data = list(range(1, array_for_test + 1))
while True:

print("Select an operation: I - Insert value, S - Search, D - Delete, Z - Exit")

d = input().lower()

if d == 'i':

add(data)

elif d == 'd':

delete(data)

elif d == 's':

print('Enter a value to search for:')

n = int(input())

start = time.perf_counter()

InterpolationSearch(data, n)

end = time.perf_counter()

print(f"InterpolationSearch: {end-start}")

start = time.perf_counter()

stdSearch(data, n)

end = time.perf_counter()

print(f"stdSearch: {end-start}")

elif d == 'z':

break

if __name__ == '__main__':

main()

Результат работы программы:

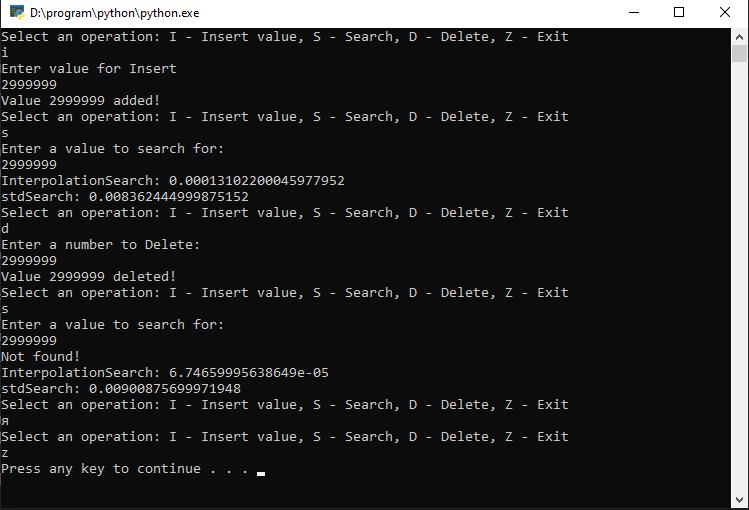
Таблица сравнения скорости поиска:

Метод поиска	Интерполяционный, сек	Стандартный Python, сек
Размер массива	Интерполяционный, сек	Стандартный Python, сек
50000	0,000386	0.00879
500000	0.000131	0.00836
5000000	0.000109	0.082
500000000	0,039	1016

Вывод

Исходя из полученных данных, время стандартного поиска в Python пропорционально зависит от размера массива: больше массив – больше время поиска. Так же он быстрее интерполяционного поиска. Интерполяционный поиск, в свою очередь, не зависит от размера массива, он вычисляет вероятность нахождения искомого значения по формуле и эти значения всегда примерно равны.

Был произведен дополнительный замер скорости с размером массива 500000000, в этом случае интерполяционный метод поиска показал свою эффективность.
Часть 2.

В соответствии с заданием разработан алгоритм хэширования массива методом цепочек. Хеширование производится с помощью функции, в которую передается ключ, после чего он умножается на 3, а затем берется остаток от деления полученного числа на 7. Ключом выступают случайные числа от 20 до 30. Реализованы функции добавления и удаления данных в хэш-таблицу по ключу, а также поиск по ключу и увеличение размера массива путем рехэширования.

Код программы представлен ниже:

import random
def hash_function(key):

return (key * 3) % 7
def add(key, value, hash_table):

index = hash_function(key)

max_size = 10

if len(hash_table[index]) < max_size:

hash_table[index].append((key, value))

print(f'Value {value} with key {key} added!')

else:

hash_table = resize(hash_table)

add(key, value, hash_table)

print(f'Value {value} with key {key} added!')

def delete(key, hash_table):

index = hash_function(key)

i = 0

found = False

while key in [item[0] for item in hash_table[index]]:

if hash_table[index][i][0] == key:

print(f'Value {hash_table[index][i][1]} deleted by key {key} !')

del hash_table[index][i]

found = True

else:

i += 1

if not found:

print(f'No value found by key {key}!')
def Search(key, hash_table):

index = hash_function(key)

found = False

for item in hash_table[index]:

if item[0] == key:

print('Value found:', item[1])

found = True

if not found:

print(f'No value found by key {key}!')
def resize(hash_table):

old_size = len(hash_table)

new_size = old_size * 2

new_table = [[] for _ in range(new_size)]

for index in range(old_size):

for item in hash_table[index]:

key = item[0]

value = item[1]

new_index = hash_function(key) % new_size

new_table[new_index].append((key, value))

return new_table
def main():

array_count = 10

hash_table = [[] for _ in range(array_count)]

for _ in range(array_count):

k = random.randint(20, 30)

v = random.randint(300, 400)

add(k, v, hash_table)
while True:

print("Enter an operation: I - Insert value, S - Search, D - Delete, V - Show all values, X - Exit")

d = input().lower()

if d == 'i':

print('Enter a value to insert:')

value = int(input())

print('Enter a key to insert:')

key = int(input())

add(key, value, hash_table)

elif d == 'd':

print('Enter a key to delete:')

key = int(input())

delete(key, hash_table)

elif d == 's':

print('Enter a key to search:')

key = int(input())

Search(key, hash_table)

elif d == 'v':

print(hash_table)

elif d == 'x':

break

if __name__ == '__main__':

main()

Результат работы программы:

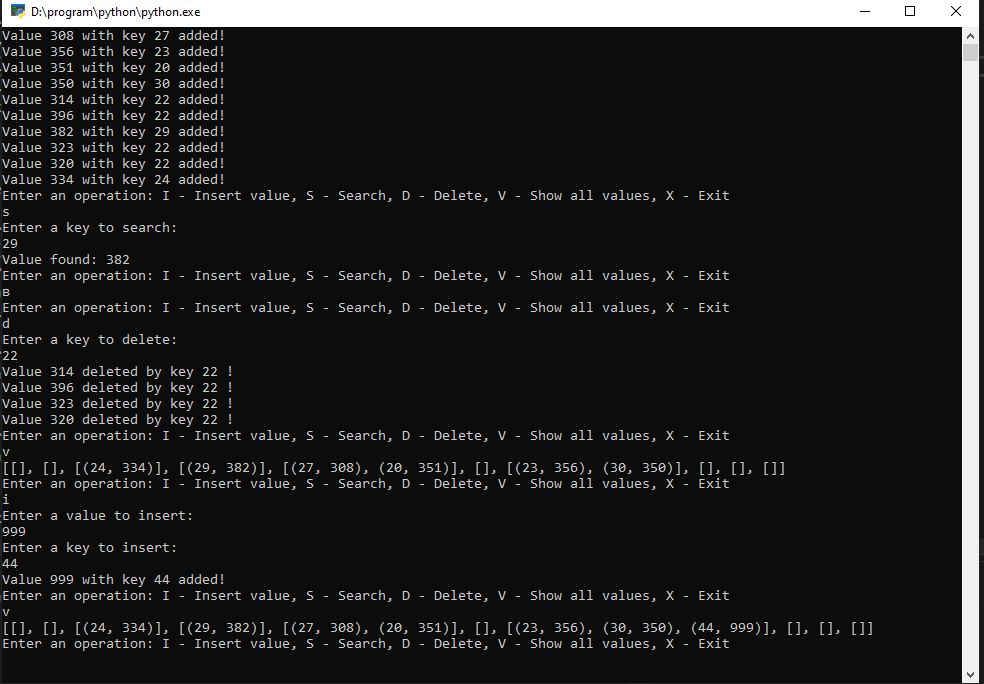
Задание №3

Цель работы
Реализовать заданный метод поиска подстроки в строке в соответствии с индивидуальным заданием. Для всех вариантов добавить реализацию добавления строк, ввода подстроки и поиска подстроки. Предусмотреть возможность существования пробела. Ввести опцию чувствительности / нечувствительности к регистру. Оценить время работы каждого алгоритма поиска и сравнить его со временем работы стандартной функции поиска, используемой в выбранном языке программирования.
Вариант 6

Метод поиска: Кнута-Морриса-Пратта.
Ход работы
В соответствии с заданием реализован алгоритм поиска Кнута-Морриса-Пратта. Разработана возможность добавлять строку, вводить подстроку и искать ее в строке. Пробел считается как отдельный символ. Текст при вводе преобразовывается к одному регистру.

Код программы:

import time
def prefix_function(pattern):

m = len(pattern)

pi = [0] * m

k = 0

for q in range(1, m):

while k > 0 and pattern[k] != pattern[q]:

k = pi[k - 1]

if pattern[k] == pattern[q]:

k += 1

pi[q] = k

return pi
def kmp_search(pattern, text):

n = len(text)

m = len(pattern)

pi = prefix_function(pattern)

q = 0

found = False

for i in range(n):

while q > 0 and pattern[q] != text[i]:

q = pi[q - 1]

if pattern[q] == text[i]:

q += 1

if q == m:

q = pi[q - 1]

found = True
if not found:

print('Substring not found!')
def std_search(pattern, text):

index = text.find(pattern)

found = False

while index != -1:

index = text.find(pattern, index + 1)

found = True
if not found:

print('Substring not found!')
def main():

# text = 'The Great Attractor is a purported gravitational attraction in intergalactic space and the apparent central gravitational point of the Laniakea Supercluster.'

print('Enter a string: ')

# text = str(input().lower())

text = str(input())

pattern = ''
while True:

print('---------------------------------')

if pattern != '':

print('Current substring: ', pattern)
print('Enter an operation: F - Search , I - Insert, C - Change, X - Exit')

d = input().lower()

if d == 'f':

if pattern == '':

print('Enter a substring to search for:')

#pattern = str(input().lower())

pattern = str(input())

start = time.perf_counter()

kmp_search(pattern, text)

end = time.perf_counter()

print(f"kmp_search: {(end-start)*1000:.3f} ms")
start = time.perf_counter()

std_search(pattern, text)

end = time.perf_counter()

print(f"std_search: {(end-start)*1000:.3f} ms")

elif d == 'i':

print('Enter a substring:')

#pattern = str(input().lower())

pattern = str(input())

elif d == 'c':

print('Enter a new string:')

#text = str(input().lower())

text = str(input())

elif d == 'x':

break

if __name__ == '__main__':

main()

Смотрите также файлы

Неравенства, решаемые методом рационализации httpsshkolkovo netcatalogreshenie neravenstv metodom racionalizacii.docx

Практическая работа к теме Семья традиции.docx

Решение экрана, тип локомотива и нажать кнопку Запуск тренажёра.rtf

Планирование потребностей в материальных ресурсах и персонале службы.docx

Методические указания студенту по выполнению программы преддипломной практики.docx

Файл: Отчет по курсовой работе по предмету Сиаод Вариант х студент группы Москва 2023.docx

Оглавление

Задание №1

Задание №2

Задание №3

Смотрите также файлы

Информация

Списки файлов

Дополнительно