Файл: Отчет по курсовой работе по предмету Сиаод Вариант х студент группы Москва 2023.docx
Добавлен: 11.12.2023
Просмотров: 179
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Результат работы программы:
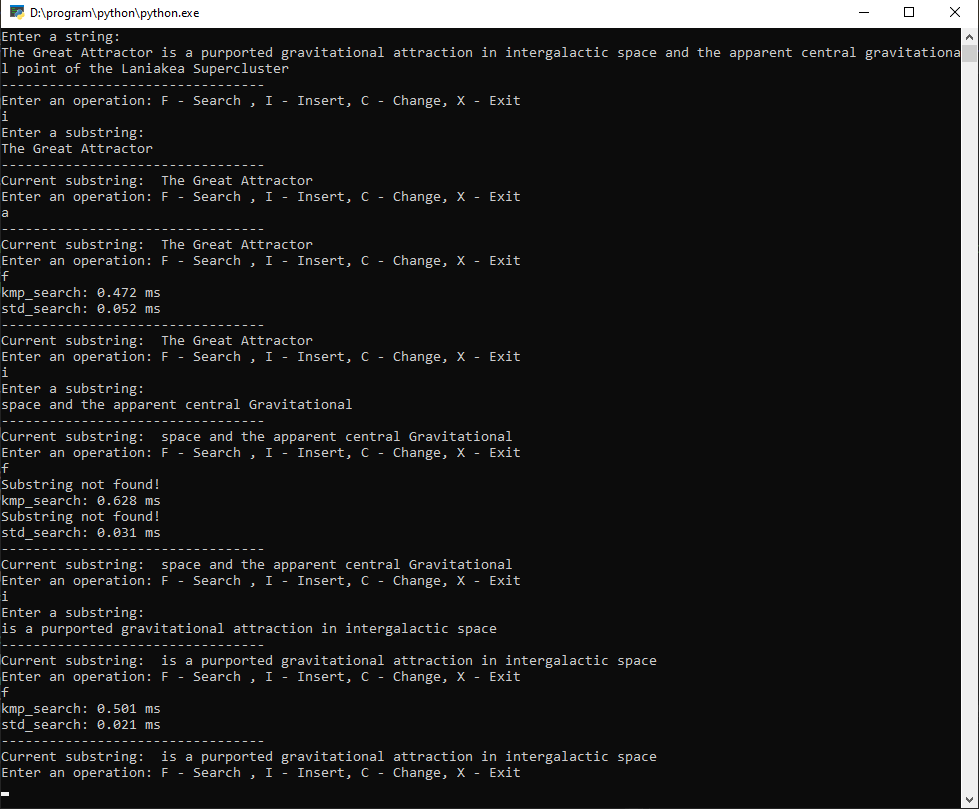
В следующей таблице представлено время поиска подстрок в строке: «The Great Attractor is a purported gravitational attraction in intergalactic space and the apparent central gravitational point of the Laniakea Supercluster.»
| Подстрока | Алгоритм КМП, мс | Встроенный алгоритм Python, мс |
| The Great Attractor | 0,472 | 0,052 |
| space and the apparent central Gravitational (ненайдено) | 0,628 | 0,031 |
| is a purported gravitational attraction in intergalactic space | 0,501 | 0,021 |
Вывод
Исходя из полученных данных, стандартный поиск подстроки в строку, встроенный в Python, гораздо быстрее чем алгоритм Кнута-Морриса-Пратта.
Задание №4
Цель работы
Используя технологию модульного программирования разработать программу обработки данных, содержащихся в заранее подготовленном файле, в соответствии с индивидуальным заданием. Применить динамическую структуру указанного в задании вида: стек, очередь или дек. Программа должна включать модуль, содержащий набор всех необходимых средств (типов, подпрограмм и т.д.) для решения поставленной задачи.
Вариант 6
Дан файл из вещественных чисел. Используя стек за один просмотр файла напечатать сначала все числа, меньшие a, затем все числа из интервала [a,b], и, наконец, все остальные числа, сохраняя исходный порядок в каждой группе.
Ход работы
Ниже представлен основной код программы. Чтобы сохранить исходный порядок чисел в каждой группе, каждая группа будет вноситься в отдельный стек.
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 | my_stack_beforeA = [] my_stack_inAB = [] my_stack_afterB = [] my_stack = [] def write_my_stack (item, value_from_file): item.append (value_from_file) print('Enter the value A:') vA = float(input()) print('Enter the value B:') vB = float(input()) file_of_values = open('d:\data.txt', 'rt') for lines in file_of_values: strings = lines.split(' ') for substring in strings: if substring != '': my_data = float(substring) write_my_stack (my_stack, my_data) if my_data < vA: write_my_stack (my_stack_beforeA, my_data) else: if (my_data >= vA) and (my_data <= vB): write_my_stack (my_stack_inAB, my_data) else: write_my_stack (my_stack_afterB, my_data) if len(my_stack_beforeA) == 0: print ('Stack my_stack_beforeA is empty') else: print ('Values before A ', my_stack_beforeA) if len(my_stack_inAB) == 0: print ('Stack my_stack_inAB is empty') else: print ('Values in the interval A:B ', my_stack_inAB) if len(my_stack_afterB) == 0: print ('Stack my_stack_afterB is empty') else: print ('Values greater than B ', my_stack_afterB) print ('The original contents of the file ', my_stack) |
Результат выполнения кода:
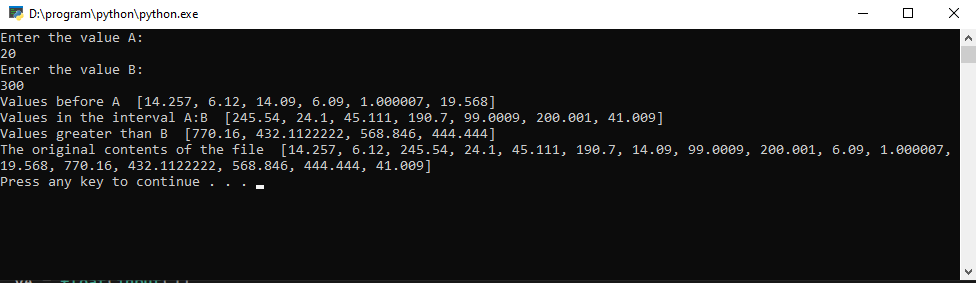
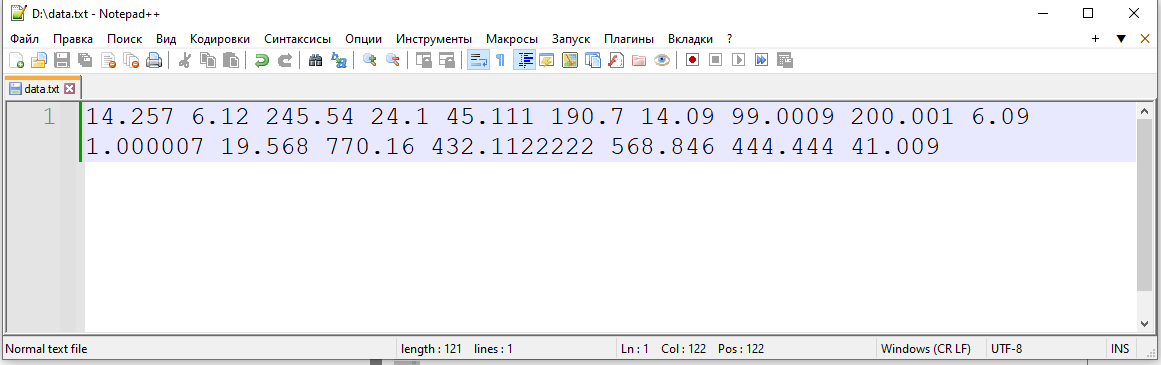
Изначальный порядок расположения чисел:
Задание №5
Цель работы
Реализовать генерацию заданного типа фрактала с применением рекурсивных функций. Добавить возможность задания глубины фрактала. Оценить глубину рекурсии. Построить таблицу зависимости времени построения от глубины фрактала.
Вариант 6
Реализовать генерацию фрактала «Дерево Пифагора».
Выполнение
Г
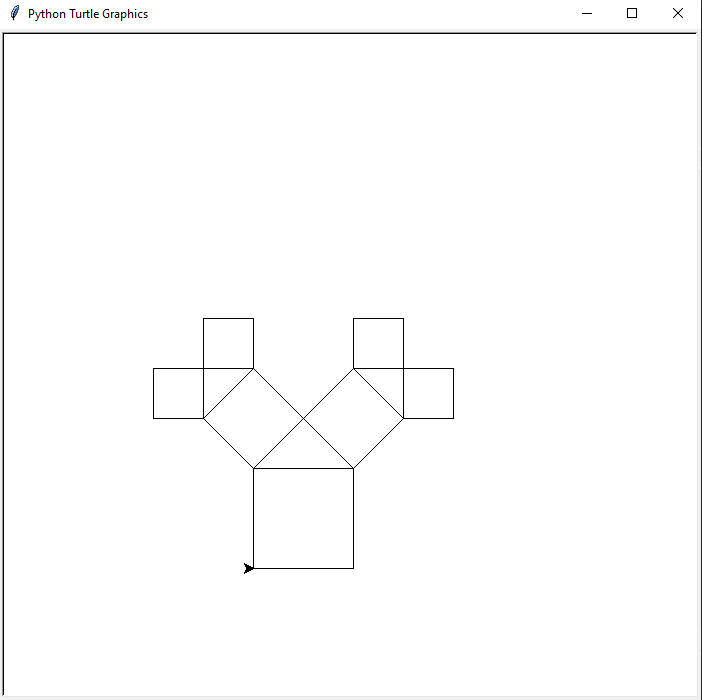
лубина 2:
Г
лубина 7:
Глубина 11:
Код программы:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 | from __future__ import print_function import turtle import time LIMIT = 7 SCALAR = 0.5 ** 0.5 INDENT = ' ' * 4 def drawTree(size, depth, branch): print(INDENT * depth, branch, depth, 'start') drawSquare(size) if depth + 1 <= LIMIT: t.left(90) t.forward(size) t.right(45) drawTree(size * SCALAR, depth + 1, 'left ') t.forward(size * SCALAR) t.right(90) drawTree(size * SCALAR, depth + 1, 'right') t.left(90) t.backward(size * SCALAR) t.left(45) t.backward(size) t.right(90) print(INDENT * depth, branch, depth, 'stop') def drawSquare(sideLength): t.down() for i in range(4): t.forward(sideLength) t.left(90) t.up() t = turtle.Pen() t.up() t.goto(-100, -200) start = time.perf_counter() drawTree(100.0, 0, 'root') end = time.perf_counter() print(end-start) turtle.mainloop() |
Результаты работы:
| Глубина фрактала | 2 | 7 | 11 |
| Время выполнения, сек | 9 | 305 | 5140 |
Вывод
Реализовали генерацию фрактала «Дерево Пифагора» с применением рекурсивных функций. Из результатов тестов сделали вывод, что «Дерево Пифагора» несложный фрактал на низких глубинах, и становится сложнее с большими глубинами.