Файл: Метод Крамера и его возможности.docx

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа с углубленным изучением отдельных предметов с. Тербуны Тербунского муниципального района

Липецкой области

ИТОГОВЫЙ ИНДИВИДУАЛЬНЫЙ ПРОЕКТ
по теме
«Метод Крамера и его возможности»

Выполнила: Волочаева Дарья, ученица 10а класса

Руководитель: Орлова Е.И., учитель математики

Тербуны

2021

1

1.Введение 3

2.Теоретическая часть 5

2.1. Исторические сведения 5

2.2. Определители n-ого порядка 5

2.3. Вычисление определителей третьего порядка 6

2.4. Решение систем линейных уравнений методом Крамера 6

2.5. Решение систем уравнений с параметром 10

3.Практическая часть 11

4.Заключение 13

5.Список используемой литературы 15

6.Приложение I

I

I

Объяснение способа решения систем линейных уравнений методом Крамера. I

II

II

Проведение самостоятельной работы. II

III

1.Введение

Миллионы людей занимаются математическими расчетами, иногда в силу влечения к таинствам математики и ее внутренней красоте, а чаще в силу профессиональной или жизненной необходимости, не говоря уже об учебе.

При конструировании инженерных сооружений, обработке результатов измерений, решении задач планирования производственного процесса и ряда других задач техники, экономики, научного эксперимента приходится решать системы линейных уравнений.

Способов решения систем уравнений существует много: сложения, подстановки, графический, методом исключения неизвестных. При решении систем линейных уравнений в школе на уроках алгебры, мы использовали такие способы, как сложение, подстановка и графический. Каждый способ удобен для определенной системы.

К примеру, систему

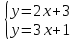
можно решить графическим способом.

Систему:

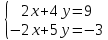
без труда решим способом сложения.

Система:

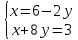
проще всего решается подстановкой.

В справочнике по математике мне встретился метод Крамера, который используется для решения систем линейных уравнений, но не изучается в школе. Я заинтересовалась этим методом, поэтому я решила самостоятельно изучить метод Крамера, который подходит для решения систем линейных уравнений с большим количеством неизвестных.

Мне захотелось научиться решать системы, состоящие из 3-х уравнений с тремя неизвестными, разными способами, что может помочь в решении более сложных задач не только в математике, в экономике, в олимпиадных работах и при сдаче ЕГЭ.
Актуальность темы:

Использование полученного опыта решения систем линейных уравнений с помощью определителей способствует развитию логической культуры.
Применение систем линейных уравнений мы можем встретить в различных областях науки.
Системы линейных уравнений встречаются на экзаменах, и умение решать их несколькими способами значительно увеличивает шанс справиться с заданием.

Цель:

Исследование методов решения систем линейных алгебраических уравнений с помощью метода Крамера.
Задачи:

Изучить историю метода Крамера.
Познакомиться с методом Крамера для решения систем линейных уравнений.
Научиться решать системы линейных уравнений методом Крамера.
Разработать и провести занятия с одноклассниками по знакомству с методом Крамера и определить уровень усвоения.

Объект исследования: Метод Крамера.

Предмет исследования: Системы линейных уравнений, решаемые методом Крамера.

Методы исследования: Сравнение, анализ, обобщение, эксперимент.

Гипотеза: Использование данного метода увеличивает эффективность решения систем линейных уравнений.

Практическая значимость: Материал этого исследования может быть использован на дополнительных занятиях по математике и для самостоятельной подготовки к олимпиадам и ЕГЭ.

2.Теоретическая часть

2.1. Исторические сведения

Габриэль Крамер родился 31 июля 1704 года в Женеве (Швейцария). Уже в детстве он опережал своих сверстников в интеллектуальном развитии, демонстрировал завидные способности в области математики.

В 18 лет он успешно защитил диссертацию. Через 2 года Крамер выставил свою кандидатуру на должность преподавателя в Женевском университете. Юноша так понравился магистрату, что специально для него и ещё одного кандидата на место преподавателя была учреждена отдельная кафедра математики, где Крамер и работал в последующие годы.

Крамер является одним из создателей линейной алгебры. Одной из самых известных его работ является «Введение в анализ алгебраических кривых», опубликованный на французском языке в 1750 году. В ней Крамер строит систему линейных уравнений и решает её с помощью алгоритма, названного позже его именем – метод Крамера.[6]

Метод Крамера применяется для решения систем линейных алгебраических уравнений, в которых число неизвестных переменных равно числу уравнений и определитель основной матрицы отличен от нуля.

2.2. Определители n-ого порядка

Определителем n-го порядка называется число ∆_????, составленное по определенному правилу и записываемое в виде квадратной таблицы

Где а₁₁, а₁₂, а₁₃, … - числовые коэффициенты

Значение определителя _????находится по следующему правилу.[3]

Для n = 2

Пример 1.

Вычислить определитель:

Ответ: -20
Пример 2.

Вычислить определитель:
Ответ: -36

2.3. Вычисление определителей третьего порядка

Для вычисления определителей третьего порядка существует правило треугольника.

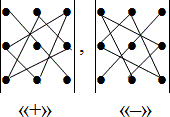Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком "плюс"; аналогично, для второго определителя - соответствующие произведения берутся со знаком "минус"[4], т.е.

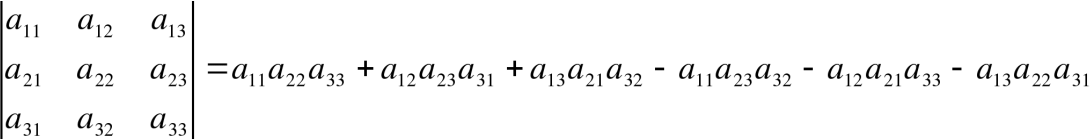
Пример 3.

Вычислить определитель методом треугольников.

Решение.

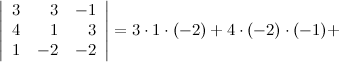
Ответ. 54

2.4. Решение систем линейных уравнений методом Крамера

Метод Крамера – это метод решения систем линейных уравнений. Он применяется только к системам линейных уравнений, в которых число уравнений совпадает с числом неизвестных и определитель отличен от нуля. Любая крамеровская система уравнений имеет единственное решение.

Решение системы двух линейных уравнений с двумя неизвестными
Сначала рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? Ведь простейшую систему можно решить школьным методом, методом сложения или подстановки. Более простой пример поможет понять, как использовать правило Крамера для более сложного случая–системы трех уравнений с тремя неизвестными. Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера.[2]

Рассмотрю систему уравнений

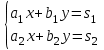
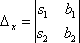
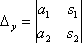
На первом шаге вычислим определитель , его называют главным определителем системы.

В случае если правило Крамера не поможет. Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя

Корни уравнения находим по формулам:

,

Пример 1.

Решить систему линейных уравнений

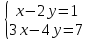
Решение: Решим систему по формулам Крамера

∆= |^{1 −2}|=1∙ (-4) - (-2) ∙3= -4+6=2 0

3 −4

Определитель ∆ 0, следовательно, заданная система может быть решена методом Крамера.

Вычислим определитель ∆_х, для этого заменим первый столбец в главном определителе на столбец свободных членов, получим

∆x= |^{1 −2}|=1∙ (-4) - (-2) ∙7 =-4+14=10

7 −4

Аналогично, заменяя второй столбец в главном определителе на столбец свободных членов, получим

∆y = | ^{1 1}|=1∙7 - 1∙3 =7-3=4

3 7

Далее по формулам Крамера находим неизвестные переменные:

х= = = 5, у= = = 2

Ответ: х=5, у=2
Решение системы трех уравнений с тремя неизвестными по формулам Крамера

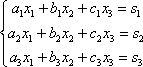Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:

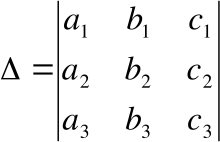Находим главный определитель системы:

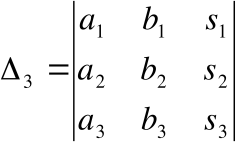
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:

, ,

И, наконец, ответ рассчитывается по формулам:

Случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.[2]

Пример 2.

Решить систему по формулам Крамера.

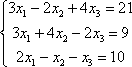
Решение: Решу систему по формулам Крамера. Обозначу главный определитель D, тогда

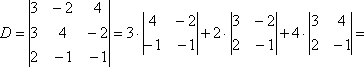
значит, система имеет единственное решение.

Ответ: х₁=5, х₂=-1, х₃=1.

Пример 3.

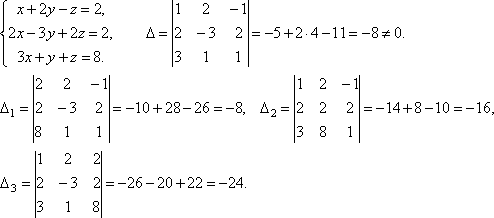ешить систему линейных уравнений методом Крамера:

Ответ: х=1, у=2, z=3.
Три случая при решении систем линейных уравнений
При решении системы линейных уравнений методом Крамера могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение (система совместна и определённа)

Условия:

Второй случай: система линейных уравнений имеет бесконечное множество решений (система совместна и неопределённа)

Условия: ,

Третий случай: система линейных уравнений решений не имеет (система несовместна)

Условия: ,

Итак, система линейных уравнений называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.[5]
Пример 4. Решить систему линейных уравнений методом Крамера:

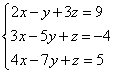
Решение. Нахожу главный определитель системы:

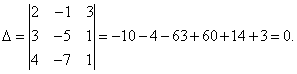
Определитель системы равен нулю, следовательно, система линейных уравнений либо имеет бесконечное множество решений, либо не имеет решений. Для уточнения вычисляю определители при неизвестных

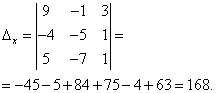
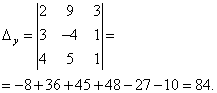
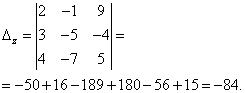
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Ответ: нет решений

2.5. Решение систем уравнений с параметром

.Найдите все значения параметра а, при которых система имеет единственное решение.[1]

Решение: Данная система имеет единственное решение при условии .

ак как = - 40-6а, то система имеет единственное решение при

а

^Ответ:^при^{система имеет единственное решение.}
2

.Найдите все значения параметра в, при которых система не имеет решений.

^{Решение:}^{= -184 + 120 =- 64 0}
^Даннаяне будет иметь решений, если

^=-8^в^{+24=0, то есть при}^в⁼³
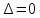
^Ответ:при в = 3 система не имеет решений.
3.Найдите все значения параметра в, при которых система

имеет бесконечно много решений
^{Р ешение}^:
то данная система имеет бесконечно много решений при условии

⁼
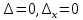
12-8в=0,-8в= -12, в =1,5 и 6-4в=0, -4в= -6, в =1,5

^Ответ:при в = 1,5 система имеет бесконечно много решений.

3.Практическая часть

Теперь, когда мне стал понятен принцип решения систем линейных уравнений методом Крамера, я решила познакомить одноклассников с новым способом решения систем линейных уравнений и проверить насколько метод Крамера понятен ученикам моего класса, и можно ли его изучать в школьной программе. Для начала я рассказала теоретический материал и объяснила способ решения системы методом Крамера. (приложение I) Затем