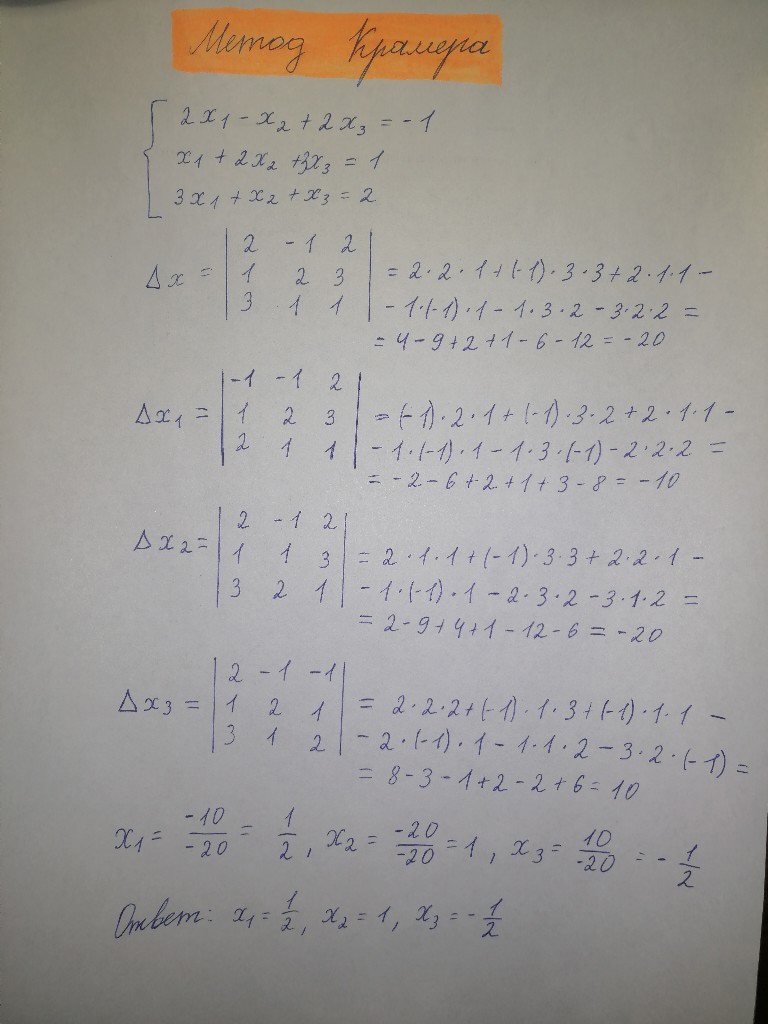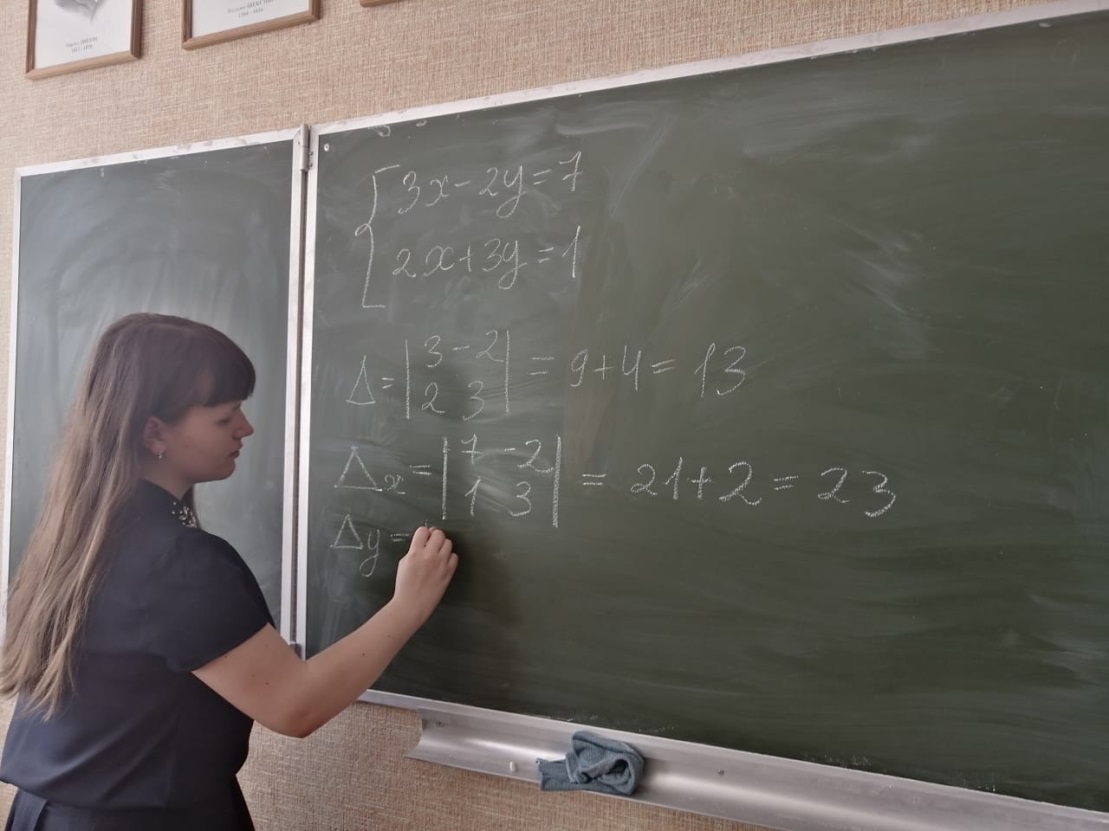ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 31
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
провела небольшую самостоятельную работу, в которой первую систему нужно было решить тремя способами (подстановкой, сложением и методом Крамера), вторую систему учащиеся могли решить любым удобным для себя способом. (Приложение II)
Пример решения системы
Решение:
 =
= 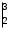
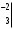 =
=  9 +4=13
9 +4=13
 x =
x = 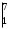
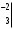 = 21+2 = 23
= 21+2 = 23
 y =
y = 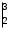
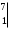 = 3-14 = -11
= 3-14 = -11
x =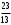 , y =
, y = 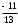
Ответ: (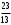 ;
; 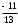 )
)
Самостоятельная работа
1.Решить систему уравнений способом сложения, подстановки и методом Крамера:
Решение системы показано в приложении ӀII
2. Решить систему уравнений любым способом:
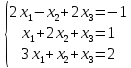
Решение системы показано в приложении ӀV
В эксперименте приняли участие 24 человека. При решении первой системы уравнений, состоящей из двух уравнений, у учащихся не возникли трудности, большинство справились с этой системой. Подстановкой правильно смогли решить систему уравнений 20 человек, сложением 22 человека, методом Крамера 17 человек (рис.1). Для решения второй системы уравнений, состоящей из трех уравнений, способ решения мог быть выбран любой. При решении этой системы уравнений у учащихся, выбравших способ постановки и сложения возникли трудности. А учащихся, использовавшие метод Крамера, почти все смогли справиться с решением данной системы. Из 20 человек, выбравших метод Крамера, 15 человек решили систему правильно (рис.2).
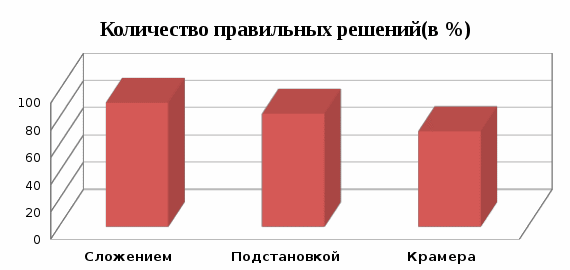
Рис.1.Количество правильных решений (в %) при решении учащихся первой системы уравнений (тремя способами)
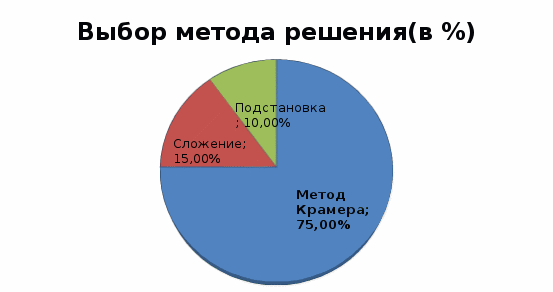
Рис.2.Выбор метода решения (в %) учащихся при решении второй системы уравнений (любым способом)
Вывод: Мои одноклассники познакомились с методом Крамера для решения систем линейных уравнений не хуже, чем методами подстановки и сложения. Первая система линейных уравнений легко решается любым из предложенных способов, но легче в вычислениях для второй системы линейных уравнений оказался метод Крамера. Более того, если есть возможность выбора способа решения, то 75% учащихся остановились на новом методе (рис.2).
С помощью дополнительной литературы я изучила метод Крамера, узнала, что такое определитель, как он находится, и научилась применять данный метод на практике. Я провела урок с одноклассниками по изучению нового метода решения систем и предложила учащимся решить системы уравнений новым методом. Большинство учащихся, воспользовавшись методом Крамера, решили системы уравнений правильно.
Перед тем, как начать писать проект, я определила для себя такие риски и сложности как: исследуемая информация может быть сложна, в связи с тем, что изучаемый мною материал выходит за рамки школьной программы. Кроме того, может возникнуть трудность при передаче информации другим учащимся в связи с моей методической неграмотностью, т.е. незнание методов изложения материала. Но риск оказался не оправдан, т.к. тема не вызвала затруднений, и я смогла преподнести информацию так, что учащиеся смогли ее реализовать.
В процессе работы над данным проектом я выполнила все поставленные перед собой задачи и достигла поставленной цели. Доказала справедливость моей гипотезы, что эффективность решения систем линейных уравнения повышается, если использовать метод Крамера.
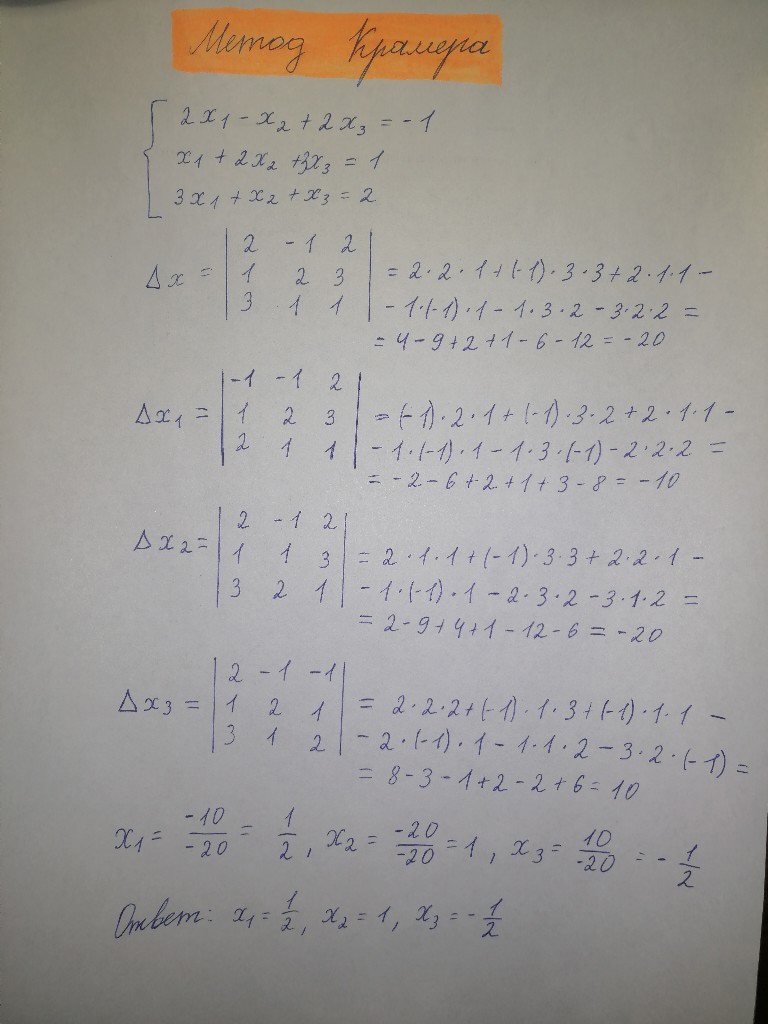
Пример решения системы
| | 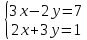 |
Решение:
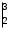
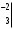 =
= 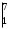
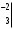 = 21+2 = 23
= 21+2 = 23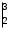
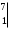 = 3-14 = -11
= 3-14 = -11x =
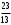 , y =
, y = 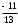
Ответ: (
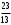 ;
; 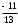 )
)Самостоятельная работа
1.Решить систему уравнений способом сложения, подстановки и методом Крамера:
| | 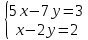 |
Решение системы показано в приложении ӀII
2. Решить систему уравнений любым способом:
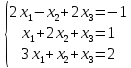
Решение системы показано в приложении ӀV
В эксперименте приняли участие 24 человека. При решении первой системы уравнений, состоящей из двух уравнений, у учащихся не возникли трудности, большинство справились с этой системой. Подстановкой правильно смогли решить систему уравнений 20 человек, сложением 22 человека, методом Крамера 17 человек (рис.1). Для решения второй системы уравнений, состоящей из трех уравнений, способ решения мог быть выбран любой. При решении этой системы уравнений у учащихся, выбравших способ постановки и сложения возникли трудности. А учащихся, использовавшие метод Крамера, почти все смогли справиться с решением данной системы. Из 20 человек, выбравших метод Крамера, 15 человек решили систему правильно (рис.2).

Рис.1.Количество правильных решений (в %) при решении учащихся первой системы уравнений (тремя способами)

Рис.2.Выбор метода решения (в %) учащихся при решении второй системы уравнений (любым способом)
Вывод: Мои одноклассники познакомились с методом Крамера для решения систем линейных уравнений не хуже, чем методами подстановки и сложения. Первая система линейных уравнений легко решается любым из предложенных способов, но легче в вычислениях для второй системы линейных уравнений оказался метод Крамера. Более того, если есть возможность выбора способа решения, то 75% учащихся остановились на новом методе (рис.2).
4.Заключение
С помощью дополнительной литературы я изучила метод Крамера, узнала, что такое определитель, как он находится, и научилась применять данный метод на практике. Я провела урок с одноклассниками по изучению нового метода решения систем и предложила учащимся решить системы уравнений новым методом. Большинство учащихся, воспользовавшись методом Крамера, решили системы уравнений правильно.
Перед тем, как начать писать проект, я определила для себя такие риски и сложности как: исследуемая информация может быть сложна, в связи с тем, что изучаемый мною материал выходит за рамки школьной программы. Кроме того, может возникнуть трудность при передаче информации другим учащимся в связи с моей методической неграмотностью, т.е. незнание методов изложения материала. Но риск оказался не оправдан, т.к. тема не вызвала затруднений, и я смогла преподнести информацию так, что учащиеся смогли ее реализовать.
В процессе работы над данным проектом я выполнила все поставленные перед собой задачи и достигла поставленной цели. Доказала справедливость моей гипотезы, что эффективность решения систем линейных уравнения повышается, если использовать метод Крамера.
5.Список используемой литературы
-
Красс, М.С., Чупрынов, Б.П. Математика для экономистов.- Текст: Учебное пособие//М.С. Красс, Б.П.Чупрынов.-М.: Издательский дом «Питер»,2005.-c.35-36.[1] -
Правило Крамера. Метод обратной матрицы. - Текст: электронный //Mathprofi.net: офиц. сайт. – URL: https://mathprofi.net/pravilo_kramera_matrichnyi_metod.html[2] -
Понятие определителя второго порядка. - Текст: электронный //Studfiles: офиц. сайт. – URL: http://www.studfiles.ru/preview/4404558/ [3] -
Понятие определителя третьего порядка. - Текст: электронный //МИЭМП: офиц. сайт. – URL: http://miemp-mi-gor.narod.ru/utcheba/matem/matrica/003.htm/[4] -
Примеры решения систем методом Крамера. - Текст: электронный // SolverBook: офиц. сайт. – URL: http://ru.solverbook.com/primery-reshenij/primery-resheniya-sistem-metodom-kramera/[5] -
Сайт с краткой биографией Г. Крамера. - Текст: электронный //Calend: офиц. сайт. – URL: https://www.calend.ru/persons/1064/[6]
6.Приложение
Объяснение способа решения систем линейных уравнений методом Крамера.
Проведение самостоятельной работы.