ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 09.01.2024
Просмотров: 97
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-






















Относительная погрешность разности в 2000 раз больше относительной погрешности суммы!
Возьмем теперь другие значения x и y и вычислим погрешности произведения и частного



Вычислим погрешности произведения и частного:














Абсолютная погрешность частного в 20000 раз больше абсолютной погрешности произведения!
Пример 6.1.2-6. Вычислить погрешности функции средствами MathCad.
-




Пусть


По приведенным начальным условиям считаем,что погрешности равны


Значение функции равно




6.1.3. Тестовые задания по теме
«Элементы теории погрешностей»
-
Погрешность числа – это
-
степень отличия приближенного значения числа от точного значения -
мера неточности числа -
мера точности числа -
процент точности числа
-
Модуль разности между точным и приближенным значением – это
-
относительная погрешность -
абсолютная погрешность -
точность -
в списке нет правильного ответа
-
Относительная погрешность выражается отношением
-
абсолютной погрешности к модулю разности приближенного и точного чисел -
модуля приближенного числа к абсолютной погрешности -
абсолютной погрешности к модулю приближенного значения -
в списке нет правильного ответа
-
Формула для определения абсолютной погрешности числа это
3)
-
Формула для определения относительной погрешности числа – это
-
Абсолютная погрешность числа измеряется
-
в долях -
в тех же единицах измерения, что и само число -
в процентах -
это безразмерная величина
-
Относительная погрешность числа измеряется
-
это безразмерная величина -
в процентах -
в процентах или долях -
в тех же единицах измерения, что и само число
-
Погрешность, обусловленная выполнением действий над данными, полученными с ограниченной точностью, это
-
погрешность округления -
погрешность метода -
в списке нет правильного ответа -
неустранимая погрешность
-
Степень отличия приближенного числа от его точного значения это
-
погрешность -
приближение -
удаление -
разность
-
При вычислении погрешности результата сложения двух приближенных чисел
-
их абсолютные погрешности вычитаются -
их абсолютные погрешности складываются -
их абсолютные погрешности делятся -
их абсолютные погрешности перемножаются
-
При вычислении погрешности результата, полученного при вычитании из одного приближенного числа другого
-
их абсолютные погрешности вычитаются -
их абсолютные погрешности делятся -
их абсолютные погрешности складываются -
их абсолютные погрешности перемножаются
-
При вычислении погрешности результата, полученного при умножении приближенных чисел друг на друга,
-
их относительные погрешности перемножаются -
их относительные погрешности вычитаются -
их относительные погрешности делятся -
их относительные погрешности складываются
-
При вычислении погрешности результата, полученного при возведении приближенного числа в степень,
-
относительная погрешность числа умножается на показатель степени -
относительные погрешности числа и показателя степени перемножаются -
относительная погрешность числа делится на показатель степени -
относительные погрешности числа и показателя степени складываются
-
Чтобы повысить точность результата вычислений численными методами, надо
-
увеличить величину заданной погрешности результата -
уменьшить величину заданной погрешности результата -
увеличить количество итераций -
в списке нет правильного ответа
-
Погрешность численного решения задачи определяется
-
обусловленностью решаемой задачи -
погрешностью представления вещественных чисел в компьютере -
чувствительностью вычислительного алгоритма к погрешностям округления -
значением исходных данных
-
Относительной погрешностью приближенного числа, для записи которого использовано выражение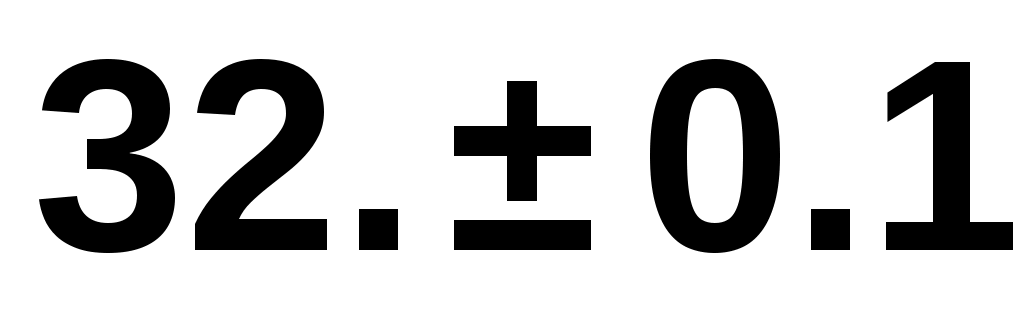 , является
, является
-
3% -
0.3201 -
320.1 -
0.003
-
Абсолютная погрешность приближенного числа 86.12, имеющего относительную погрешность 0.1%, равна
-
0.08612 -
0.008612 -
8.612 -
8.612
-
Абсолютная погрешность разности двух приближенных чисел (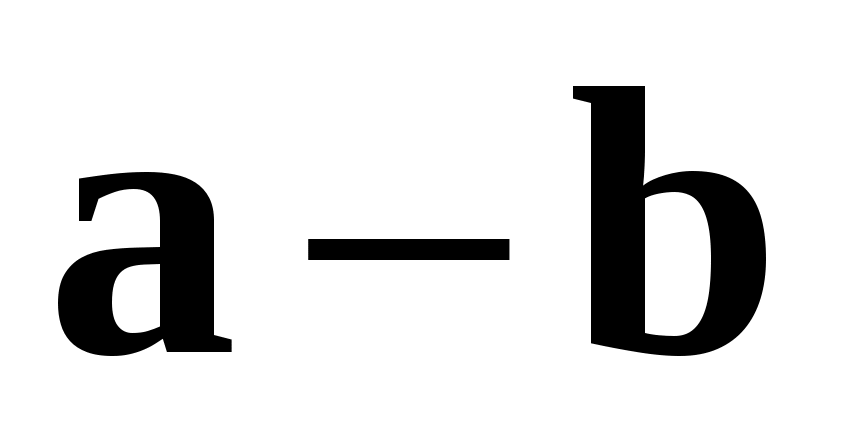 ), если
), если 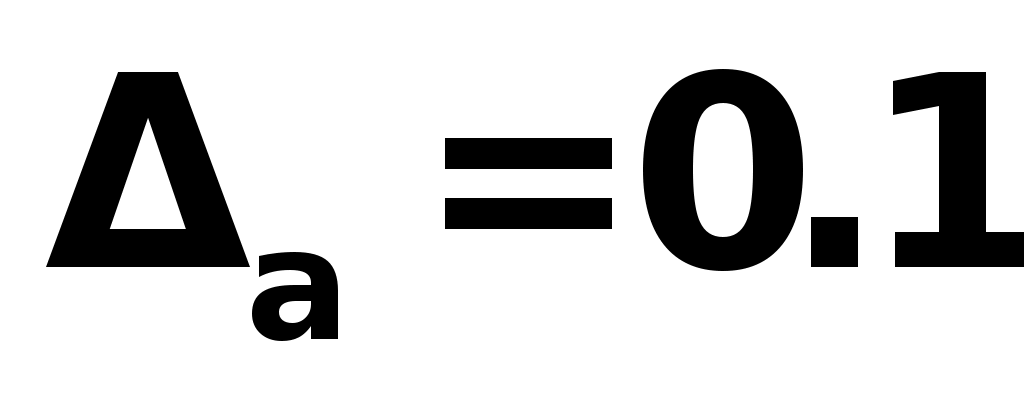 , а
, а 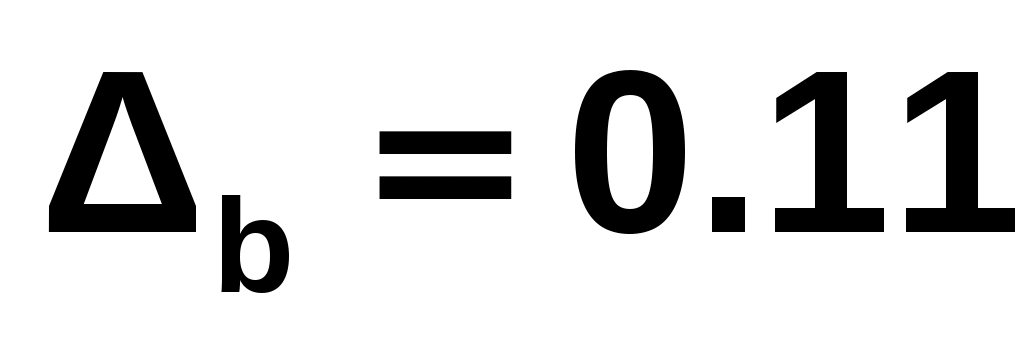 , равна
, равна
-
0.01 -
0.21 -
0.011 -
0.001
-
Абсолютная погрешность суммы двух приближенных чисел (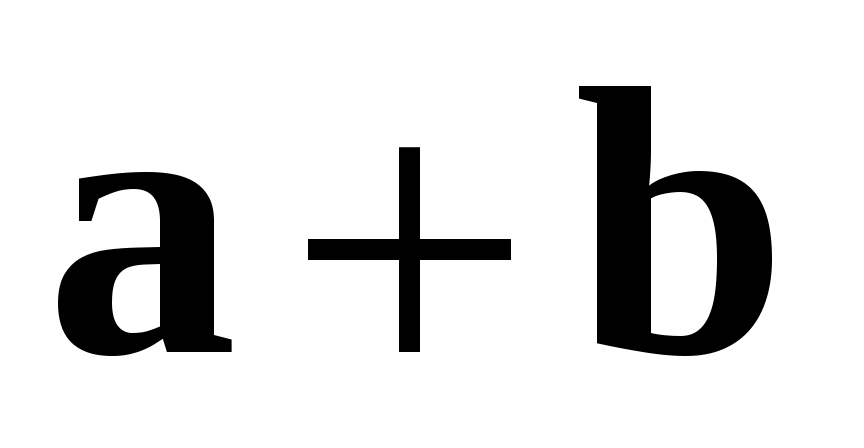 ), если
), если 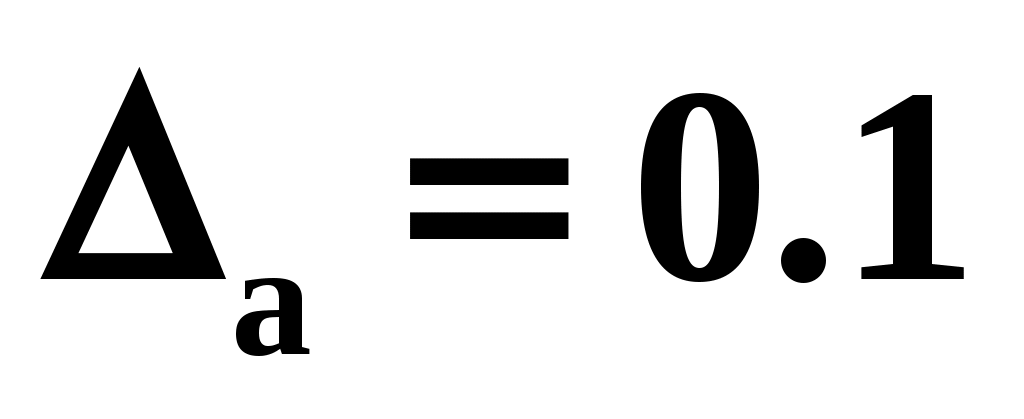 , а
, а 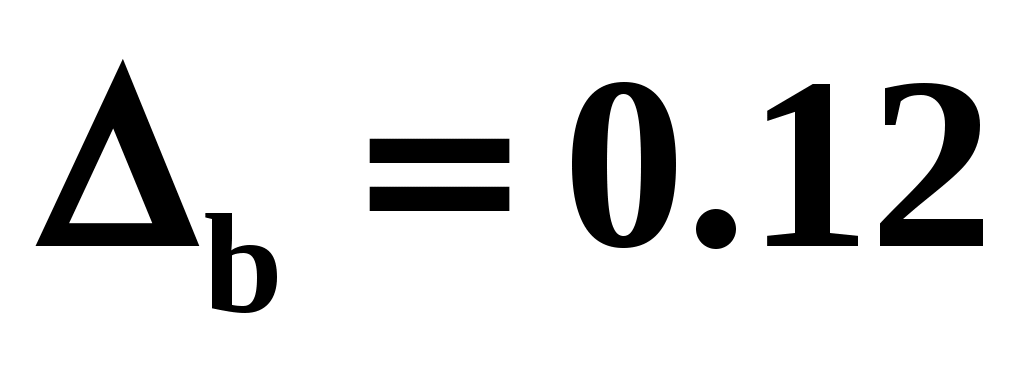 , равна
, равна
-
0.022 -
0.012 -
0.22 -
0.001
-
Относительная погрешность произведения двух приближенных чисел (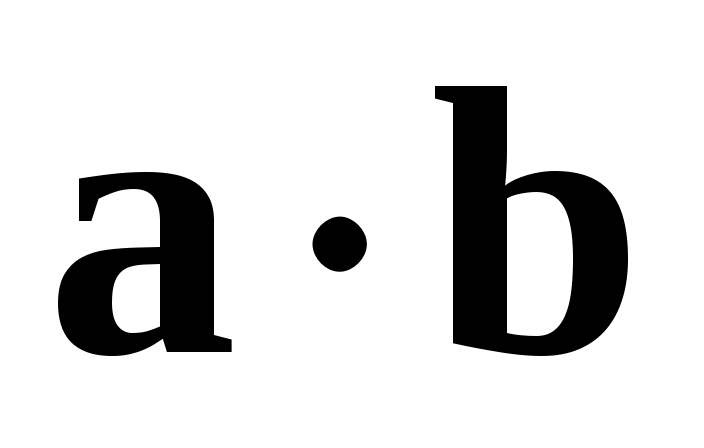 ), если
), если 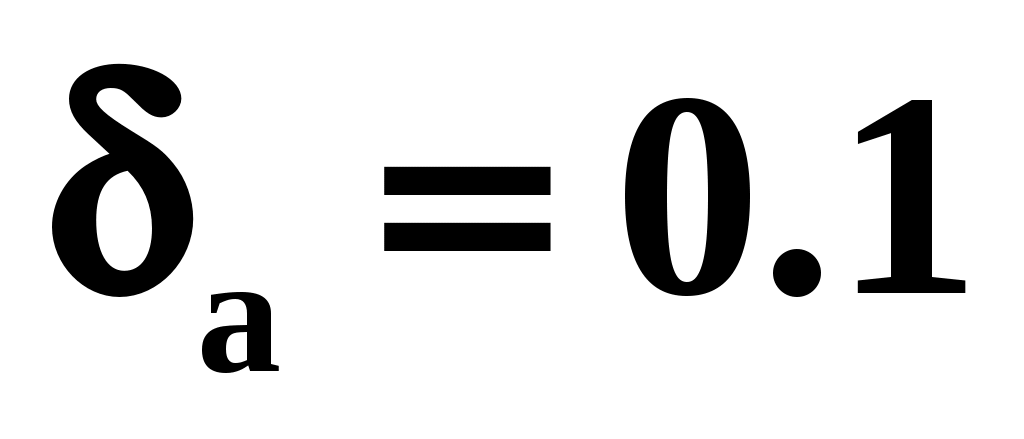 , а
, а 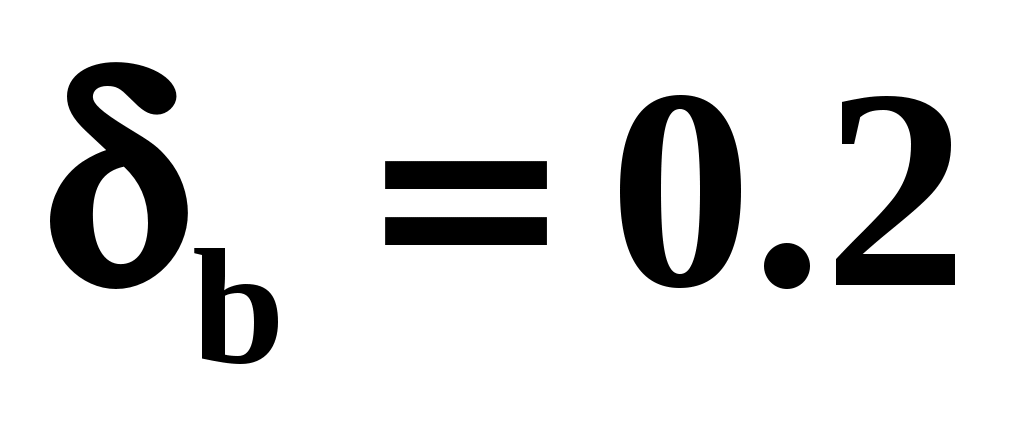 , равна
, равна
-
0.002 -
0.001 -
0.0021 -
0.3
-
Относительная погрешность частного от деления двух приближенных чисел (a/b), если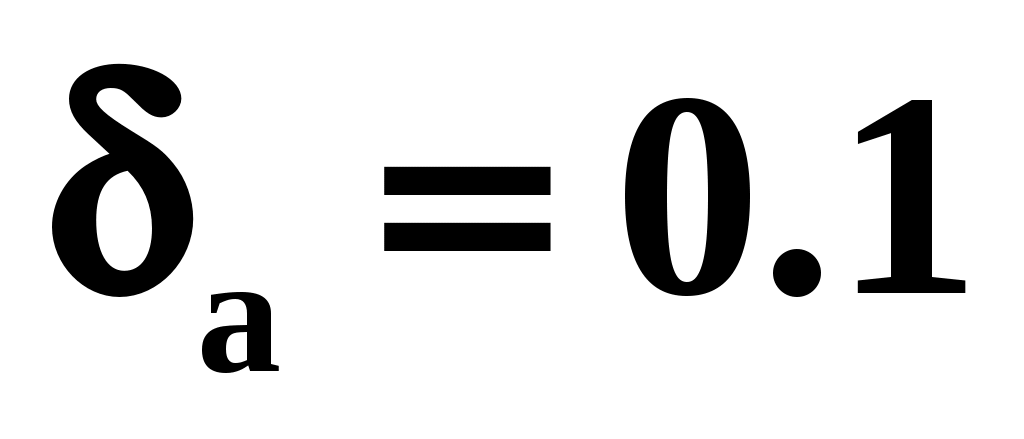 , а
, а 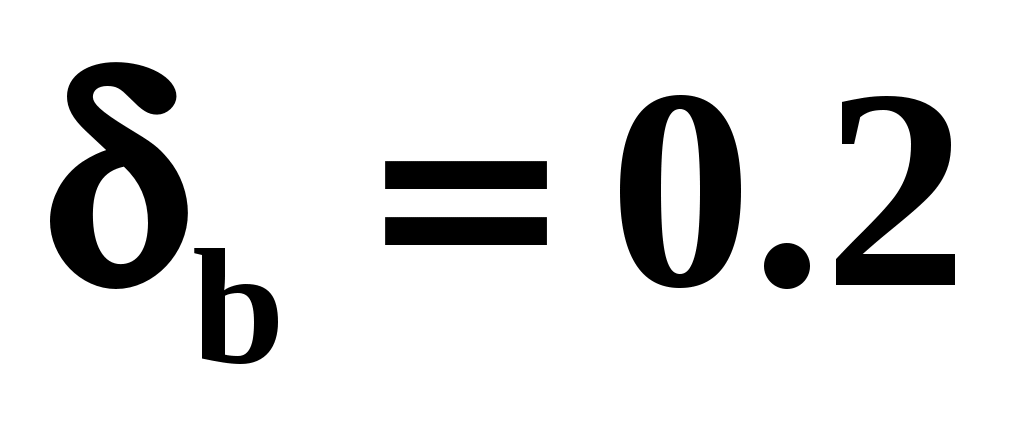 , равна
, равна
-
0.3 -
0.5 -
0.002 -
0.0021
-
Относительная погрешность результата, полученного при вычислении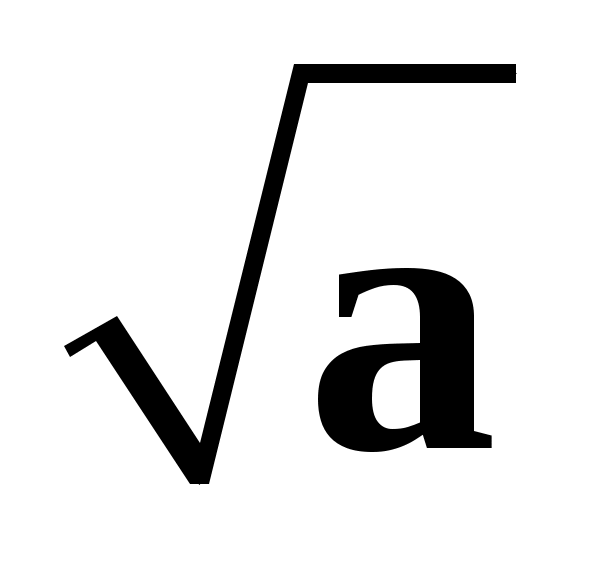 , если
, если 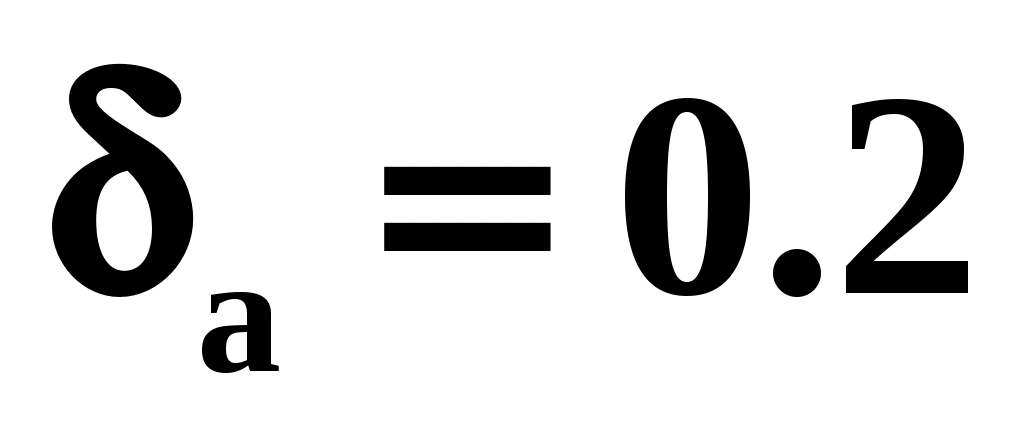 , равна
, равна
-
0.4 -
0.1 -
0.003 -
0.002
Тема 6.1. Элементы теории погрешностей Страница