Файл: Контрольная работа По дисциплине Техническая механика Тема Вариант 8 Абрамчик Татьяна Николаевна студент 2 курса группы.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 59
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение
1. Рассмотрим равновесие балки АВ. На неё действует равнодействующая Q распределённой на отрезке ЕК нагрузки интенсивности q, приложенная в середине этого отрезка; составляющие XA и YA реакции неподвижного шарнира А; реакция RС стержня ВС, направленная вдоль этого стержня; нагрузка F, приложенная в точке К под углом
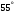 ; пара сил с моментом М (рис. 6).
; пара сил с моментом М (рис. 6).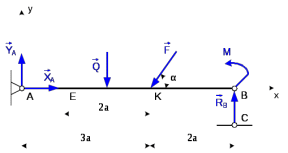
Рис. 6
2. Равнодействующая распределенной нагрузки равна:
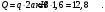
3. Записываем уравнение моментов сил, приложенных к балке АВ, относительно точки А:
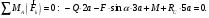 (3)
(3)4. Уравнения проекций всех сил на оси координат имеют вид:
 :
: 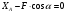 , (4)
, (4) :
: 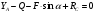 , (5)
, (5)Из уравнения (3) находим реакцию RС стержня ВС:
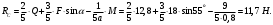
По уравнению (4) вычисляем составляющую XA реакции неподвижного шарнира А:
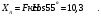
С учетом этого, из уравнения (5) имеем:
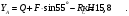
Тогда реакция неподвижного шарнира А равна:
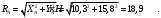
Задача 6
| Дано: |
| Найти: |
Решение
1. Поскольку маховик вращается равноускоренно, то точки на ободе маховика вращаются по закону:
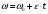 (11)
(11)По условию задачи маховик в начальный момент находился в покое, следовательно,
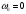 и уравнение (11) можно переписать как
и уравнение (11) можно переписать как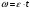 (12)
(12)2. Определяем угловую скорость вращения точек обода маховика в момент времени
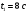 :
: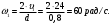
3. Находим угловое ускорение вращения маховика из уравнения (12):
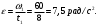
4. Вычисляем угловую скорость вращения точек обода маховика в момент времени
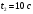 :
: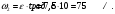
5. Тогда частота вращения маховика в момент времени
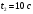 равна:
равна: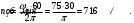
6. По формуле Эйлера находим скорость точек обода маховика в момент времени
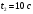 :
: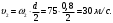
7. Определяем нормальное ускорение точек обода маховика в момент времени
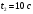 :
: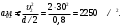
8. Находим касательное ускорение точек обода маховика в момент времени
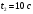 :
: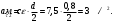
Задача 7
| Дано: | 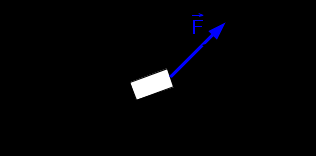 Рис. 9 |
Решение
1. Работа силы F определяется по формуле:
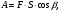 (13)
(13)где
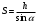 – перемещение груза.
– перемещение груза.2. По условию задачи груз перемещается с постоянной скоростью, поэтому ускорение груза
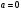 .
.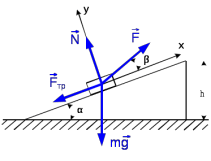
Рис. 10
3. Выбираем систему координат, направляя ось х вдоль линии движения груза. Записываем уравнения движения груза под действием сил (рис. 10):
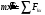 :
: 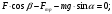 (14)
(14)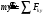 :
: 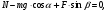 (15)
(15)где
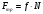 – сила трения скольжения.
– сила трения скольжения.Выражаем из уравнения (14) реакцию
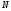 наклонной плоскости
наклонной плоскости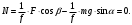
и подставляем в уравнение (15), получаем
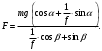
Тогда работа силы F равна
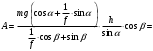
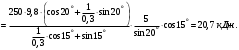
4. Мощность, развиваемая за время перемещения
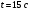 , определяется по формуле:
, определяется по формуле: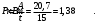 Размеще
Размещено на Список использованной литературы:
-
Аркуша А.И. Техническая механика и сопротивление материалов: Учебник для машиностроительных специальностей техникумов / А. И. Аркуша. - 2-е изд., доп. . - М.: Высшая школа, 1989. - 352 с. -
Никитин Е.М. Теоретическая механика для техникумов. М., 1969г., 432 с. -
Сетков В.И.: Сборник задач для расчетно-графических работ по технической механике: Учеб. Пособие для техникумов. 2-е изд., доп. - М.: Стройиздат, 1989,-224 с. -
Олофинская В.П. Техническая механика курс лекций с вариантами практических работ и тестовых заданий. М. Форум - ИНФРА-М. 2003г. 348стр. (электронная версия).