Файл: Контрольная работа По дисциплине Техническая механика Тема Вариант 8 Абрамчик Татьяна Николаевна студент 2 курса группы.rtf
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 64
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. В.Г.ШУХОВА»
(БГТУ им. В.Г. Шухова)
Кафедра (Русского языка)
Контрольная работа
По дисциплине: Техническая механика
Тема:
«Вариант __8___
Выполнил: Абрамчик Татьяна
Николаевна
студент 2 курса группы ЭКзд-211
Института заочного образования
Проверил:
Белгород, 2023
Содержание:
Введение 2
Задача №1. 4
Задача №2. 5
Задача №3. 7
Задача №4. 10
Задача 5 14
Задача 6 18
Задача 7 20
но на Список использованной литературы: 22
Введение
1. Техническая механика – дисциплина, вмещающая в себя основные механические дисциплины: теоретическую механику, сопротивление материалов, теорию машин и механизмов, детали машин и основы конструирования.
Техническая механика – это наука, изучающая общие законы механического движения и механического взаимодействия материальных тел.
Основные понятия и аксиомы статики
Техническая механика — комплексная дисциплина. Она включает три раздела: «Техническая механика», «Сопротивление материалов», «Детали машин». « Техническая механика» — раздел, в котором излагаются основные законы движения твердых тел и их взаимодействия. В разделе «Сопротивление материалов» изучаются основы прочности материалов и методы расчетов элементов конструкций на прочность, жесткость и устойчивость под действием внешних сил. В заключительном разделе «Технической механики» «Детали машин» рассматриваются основы конструирования и расчета деталей и сборочных единиц общего назначения.
Дисциплина «Техническая механика» является общепрофессиональной, обеспечивающей базовые знания при усвоении специальных дисциплин, изучаемых в дальнейшем.
Задачи технической механики:
Техническая механика наука о механическом движении материальных твердых тел и их взаимодействии. Механическое движение понимается как перемещение тела в пространстве и во времени по отношению к другим телам, в частности к Земле.
Для удобства изучения техническую механику подразделяют на статику, кинематику и динамику.
Статика изучает условия равновесия тел под действием сил.
Кинематика рассматривает движение тел как перемещение в пространстве; характеристики тел и причины, вызывающие движение, не рассматриваются.
Динамика изучает движение тел под действием сил.
В отличие от физики техническая механика изучает законы движения некоторых абстрактных абсолютно твердых тел: здесь материалы, форма тел существенного значения не имеют. При движении абсолютно твердое тело не деформируется и не разрушается. В случае, когда размерами тела можно пренебречь, тело заменяют материальной точкой. Это упрощение, принятое в технической механике, значительно облегчает решение задач о движении.
Задача №1.
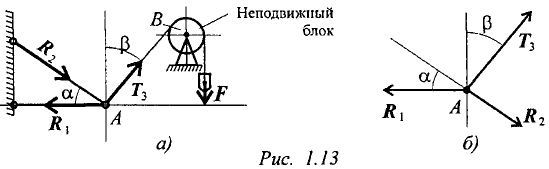
Груз подвешен на стержнях и канатах и находится в равновесии (рис. 1.13). Изобразить систему сил, действующих на шарнир
Решение:
-
Реакции стержней направлены вдоль стержней, реакции гибких связей направлены вдоль нитей в сторону натяжения (рис. 1.13а). -
Для определения точного направления усилий в стержнях мысленно убираем последовательно стержни 1 и 2. Анализируем возможные перемещения точки . Неподвижный блок с действующими на него силами не рассматриваем.
. Неподвижный блок с действующими на него силами не рассматриваем. -
Убираем стержень 1. точка поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене.
поднимается и отходит от стены, следовательно, реакция стержня 1 направлена к стене. -
Убираем стержень 2, точка поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз.
поднимается и приближается к стене, следовательно, реакция стержня 2 направлена от стены вниз. -
Канат тянет вправо. -
Освобождаемся от связей (рис. 1.136).
Задача №2.
Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5а).
Решение:
-
Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5а). Определяем возможные направления реакций связей «жесткие стержни».
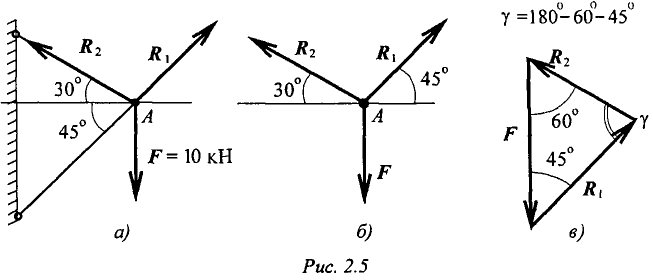
Усилия направлены вдоль стержней.
-
Освободим точку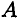 от связей, заменив действие связей их реакциями (рис. 2.56).
от связей, заменив действие связей их реакциями (рис. 2.56). -
Система находится в равновесии. Построим треугольник сил.
Построение начнем с известной силы, вычертив вектор
Из концов вектора
Пересекаясь, линии создадут треугольник (рис. 2.5в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.
-
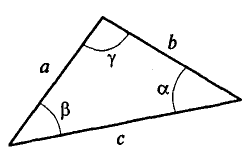
Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная
Для данного случая:
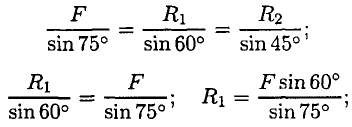
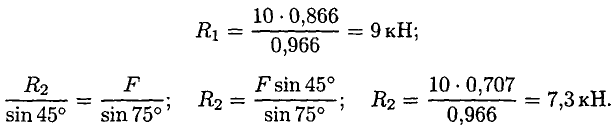
Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.
Задача №3.
Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6а).
Решение:
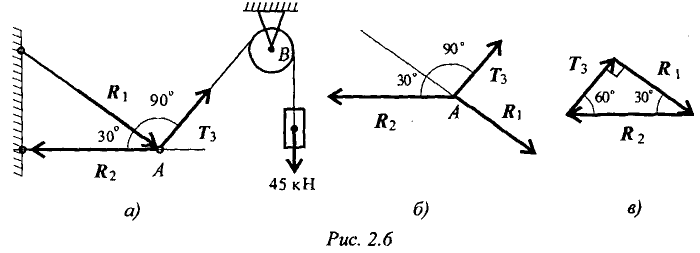
-
Нанесем на схему возможные направления усилий, приложенных в точке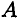 . Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки
. Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки 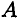 к точке
к точке 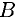 .
. -
Груз находится в равновесии, следовательно, в равновесии находится точка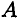 , в которой пересекаются три силы.
, в которой пересекаются три силы.
Освободим точку
Замечание. Рассмотрим только силы, приложенные к точке
-
Строим треугольник для сил, приложенных в точке , начиная с известной силы
, начиная с известной силы 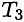 . Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке
. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке  .
.
Образовался прямоугольный треугольник (рис. 2.6в).
-
Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике:
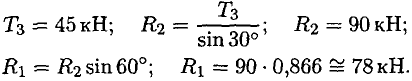
Замечание. При равновесии векторы сил в треугольнике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 1.26а. Направления совпали, следовательно, направления реакций определены верно.
Задача №4.
| Дано: Найти: | 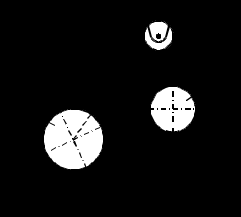 Рис. 1 |
Решение:
1. Решим задачу аналитически. Для этого рассмотрим равновесие шара 1. На него действует реакция N опорной поверхности А, перпендикулярная к этой поверхности; сила натяжения Т1 нити и вес Р1 шара 1 (рис. 2).
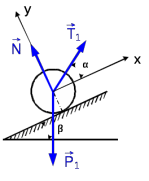
Рис. 2
Уравнения проекций всех сил, приложенных к шару 1, на оси координат имеют вид:
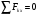 :
: 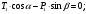 (1)
(1)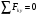 :
: 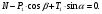 (2)
(2)Из уравнения (1) находим силу натяжения Т1 нити:
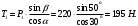
Тогда из уравнения (2) определим реакцию N опорной поверхности:
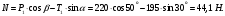
Теперь рассмотрим равновесие шара 2. На него действуют только две силы: сила натяжения Т2 нити и вес Р2 этого шара (рис. 3).
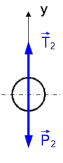
Рис. 3
Поскольку в блоке Д трение отсутствует, получаем
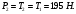
2. Решим задачу графически. Строим силовой треугольник для шара 1. Сумма векторов сил, приложенных к телу, которое находится в равновесии, равна нулю, следовательно, треугольник, составленный из
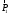 ,
, 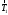 и
и 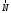 должен быть замкнут (рис. 4).
должен быть замкнут (рис. 4).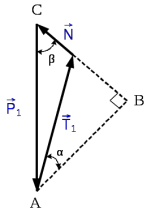
Рис. 4
Определим длины сторон силового треугольника по теореме синусов:
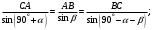
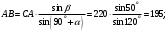
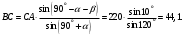
Тогда искомые силы равны:
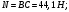
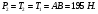
Задача 5
| Дано: Найти: | 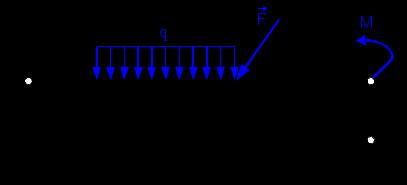 Рис. 5 |