Файл: Контрольная работа по дисциплине Эконометрика Варианттема Вариант 2 Направление подготовкиспециальность 38. 03. 01 Экономика (код, наименование).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 55
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Кафедра «__Экономика и управление_»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине:
«Эконометрика»
Вариант/тема:_Вариант № 2____
Направление подготовки/специальность_38.03.01 Экономика_______________
(код, наименование)
Обучающийся __Гаёва Милена Рамильевна_______________________________
(ФИО полностью)
Группа _ЭЗ – 301/12____ Подпись_________________
(номер группы)
Форма обучения __заочная_____________________________________________
Проверил ___________________________________________________________
(Фамилия И.О. преподавателя)
Должность __________________________________________________________
Оценка________________
Подпись _______________
Челябинск, 2023 г.
Оглавление
Введение 3
Задания 4
Заключение 10
Список литературы 11
Введение
Цель освоения дисциплины - закрепление и проверка знаний, полученных студентами в процессе самостоятельного изучения учебной литературы. Вопросы и задания, включенные в контрольную работу, предусматривают знание основных вопросов теории и умение применить их на практике решения задач.
В процессе выполнения контрольной работы у обучающихся формируются компетенции, указанные в рабочей программе дисциплины.
Задания
Задача 2
По десяти кредитным учреждениям получены данные, характеризующие зависимость объема прибыли (Y) от среднегодовой ставки по кредитам (X1), ставки по депозитам (X2) и размера внутрибанковских расходов (X3).
Требуется:
-
Осуществить выбор факторных признаков для построения двухфакторной регрессионной модели. -
Рассчитать параметры модели. -
Для характеристики модели определить:
-
линейный коэффициент множественной корреляции, -
коэффициент детерминации, -
средние коэффициенты эластичности, бетта –, дельта – коэффициенты.
Дать их интерпретацию.
-
Осуществить оценку надежности уравнения регрессии. -
Оценить с помощью t-критерия Стьюдента статистическую значимость коэффициентов уравнения множественной регрессии. -
Построить точечный и интервальный прогнозы результирующего показателя. -
Отразить результаты расчетов на графике.
Выполнение задач отразить в аналитической записке, приложить компьютерные распечатки расчетов.
| Y | X1 | X2 | X3 |
| 40 | 32 | 60 | 50 |
| 44 | 40 | 68 | 54 |
| 28 | 44 | 80 | 60 |
| 52 | 28 | 76 | 62 |
| 50 | 50 | 44 | 70 |
| 64 | 56 | 96 | 54 |
| 70 | 50 | 100 | 84 |
| 68 | 56 | 104 | 82 |
| 78 | 60 | 106 | 86 |
| 90 | 62 | 98 | 84 |
| | Y | x1 | x2 | x3 |
| Y | 1 | | | |
| x1 | 0,741326 | 1 | | |
| x2 | 0,697372 | 0,61634 | 1 | |
| x3 | 0,77753 | 0,687737 | 0,607468 | 1 |
Для выявления явления мультиколлинеарности необходимо
проанализировать коэффициенты парной корреляции между факторными
признаками.
Так как rx1x2=0,687737˂0,8, между факторными признаками х1 и х3 явление мультиколлинеарности отсутствует, все факторные признаки можно включать в модель регрессии.
В данной модели лучше оставить х1,х2. Анализ матрицы коэффициентов парной корреляции показывает ,что на зависимую переменную, т.е. на объем прибыли больше влияют ставки по кредитам (ryх1) и ставки по депозитам (ryx2).
Для построения двухфакторной регрессионной модели выбираем х1 и х2.
| ВЫВОД ИТОГОВ | | | | | | | | |
| | | | | | | | | |
| Регрессионная статистика | | | | | | | | |
| Множественный R | 0,802 | | | | | | | |
| R-квадрат | 0,643 | | | | | | | |
| Нормированный R-квадрат | 0,541 | | | | | | | |
| Стандартная ошибка | 12,823 | | | | | | | |
| Наблюдения | 10 | | | | | | | |
| | | | | | | | | |
| Дисперсионный анализ | | | | | | | | |
| | df | SS | MS | F | Значимость F | | | |
| Регрессия | 2 | 2071,381 | 1035,691 | 6,299 | 0,027 | | | |
| Остаток | 7 | 1151,019 | 164,431 | | | | | |
| Итого | 9 | 3222,400 | | | | | | |
| | | | | | | | | |
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | -9,7678 | 19,6335 | -0,4975 | 0,6341 | -56,1937 | 36,6581 | -56,1937 | 36,6581 |
| x1 | 0,8192 | 0,4678 | 1,7512 | 0,1234 | -0,2870 | 1,9254 | -0,2870 | 1,9254 |
| x2 | 0,3487 | 0,2579 | 1,3518 | 0,2185 | -0,2612 | 0,9586 | -0,2612 | 0,9586 |
На основании полученных данных можно записать уравнение:
У= - 9,767785355+0,819217395х1+0,348668195х2
Оценим качество построенной модели множественной регрессии по следующим направлениям:
Коэффициент детерминации R2 = 0,642806975 достаточно близок к 1, следовательно, качество модели можно признать высоким.
Критерий Фишера F = 6,298623574, следовательно, уравнение регрессии признается статистически значимым и может быть использовано для анализа и прогнозирования экономических процессов.
Для вычисления Fтабл необходимо определить:
-
степень свободы числителя m=2 (число факторных признаков); -
степень свободы знаменателя n-m-1=10-2-1=7; -
уровень значимости α =0,05.
Оценим качество построенной модели множественной регрессии с помощью коэффициентов эластичности, β - и ∆ - коэффициентов.
Коэффициент эластичности определяется:
Эi = bi *
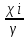 ,
,Где
Xi – среднее значение соответствующего факторного признака,
Y – среднее значение результативного признака,
Bi – коэффициенты регрессии соответствующих факторных признаков
ß – коэффициент определяется по следующей формуле:
Bi = bi *
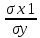
Где
σx1 – среднеквадратическое отклонение соответствующего факторного признака,
σу – СКО результативного признака.
∆ - коэффициент определяется по следующей формуле:
∆I = Bi *
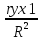
Где
ryxi – коэффициент парной корреляции результативного и соответствующего факторного признака,
R2 – коэффициент детерминации.
| | Y | x1 | x2 |
| | 40 | 32 | 60 |
| | 44 | 40 | 68 |
| | 28 | 44 | 80 |
| | 52 | 28 | 76 |
| | 50 | 50 | 44 |
| | 64 | 56 | 96 |
| | 70 | 50 | 100 |
| | 68 | 56 | 104 |
| | 78 | 60 | 106 |
| | 90 | 62 | 98 |
| | | | |
| ср. знач | 58,4 | 47,8 | 83,2 |
| эласт | | 0,670521007 | 0,6068869 |
| дисп | 358,0444444 | 134,6222222 | 442,8444444 |
| ско | -18,92206237 | 11,60268168 | 21,04386952 |
| bi | | 0,81921395 | 0,348668195 |
| Bi | | -0,502327838 | -0,387765766 |
| ryxi | | 0,741326 | 0,697372 |
| deltai | | -0,5793165 | -0,420681477 |
| R2 | 0,642806975 | | |
Частый коэффициент эластичности показывает, на сколько процентов изменится среднее значение результативного признака, если среднее значение конкретного факторного признака изменится на 1%, т.е. при увеличении на 1% среднегодовой ставки по кредитам (х1) объем прибыли увеличится на 0,6705% (Э1=0,670), при увеличении на 1% размера ставок по депозитам объем прибыли увеличится на 0,6068% (Э2=0,606).
β – коэффициент показывает, на какую величину, изменится СКО конкретного факторного признака изменится на 1 единицу, т.е. при увеличении на 1 единицу СКО ставок по кредитам, СКО объема прибыли уменьшится на – 0,50232 (β1 = -0,502), при увеличении на 1 единицу СКО ставок по депозитам СКО объема прибыли органзиции уменьшатся на 0,39 единиц (β2 = - 0,3877).
∆ - коэффициент показывает удельный вес влияния конкретного факторного признака в совместном влиянии всех факторных признаков на результативный показатель, т.е. удельный вес влияния ставок по депозитам (х2) на объем прибыли составляет – 0,42%, а удельное влияние доходов ставок по кредитам на (х1) на объем прибыли составляет – 0,58.
| | Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% |
| Y-пересечение | -9,7678 | 19,6335 | -0,4975 | 0,6341 | -56,1937 | 36,6581 | -56,1937 | 36,6581 |
| x1 | 0,8192 | 0,4678 | 1,7512 | 0,1234 | -0,2870 | 1,9254 | -0,2870 | 1,9254 |
| x2 | 0,3487 | 0,2579 | 1,3518 | 0,2185 | -0,2612 | 0,9586 | -0,2612 | 0,9586 |