ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 41
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ
Федеральное государственное образовательное бюджетное учреждение
высшего профессионального образования
«Санкт-Петербургский государственный университет телекоммуникаций
им. проф. М. А. Бонч-Бруевича»
Кафедра информационных управляющих систем
Факультет информационных систем и технологий
Лабораторная работа №1
по дисциплине
«Теория информации, данные, знания»
на тему:
«Решение СЛАУ в Scilab»
Выполнили студенты
группы ИСТ-111
Архипов С.А., Васильев И.С., Заказчик М.Н.
Принял и проверил:
Эль Сабаяр Шевченко Н.
Санкт-Петербург
2023 г
Оглавление
Формулировка задания. 3
Теоретический материал. 3
Задание 1.1. 4
Результат выполнения задания 1.1. 7
Задание 1.2. 7
Результат выполнения задания 1.2. 8
Вывод. 9
Формулировка задания.
В ходе выполнения лабораторной работы требуется решить систему линейных алгебраических уравнений (СЛАУ), используя систему компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений Scilab, а также вычислить матрицу, обратную к заданной матрице.
Теоретический материал.
Для работы с множеством данных удобно использовать массивы. Например, можно создать массив для хранения числовых или символьных данных. В этом случае вместо создания переменной для хранения каждого данного достаточно создать один массив, где каждому элементу будет присвоен порядковый номер. Таким образом, массив — множественный тип данных, состоящий из фиксированного числа элементов.
Как и любой другой переменной, массиву должно быть присвоено имя. Переменную, представляющую собой просто список данных, называют одномерным массивом, или вектором. Для доступа к данным, хранящимся в определенном элементе массива, необходимо указать имя массива и порядковый номер этого элемента, называемый индексом. Если возникает необходимость хранения данных в виде таблиц, в формате строк и столбцов, то необходимо использовать двумерные массивы (матрицы). Для доступа к данным,
хранящимся в таком массиве, необходимо указать имя массива и два индекса: первый должен соответствовать номеру строки, а второй — номеру столбца, в которых хранится необходимый элемент. Значение нижней границы индексации в Scilab равно единице. Индексы могут быть только целыми положительными числами.
Система m уравнений с n неизвестными вида:
a11 x1 + a12 x2 + · · · + a1n xn = b1 ,
a21 x1 + a22 x2 + · · · + a2n xn = b2,
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
am1 x1 + am2 x2 + · · · + amn xn = bm
называется системой линейных алгебраических уравнений (СЛАУ), причем xj —
неизвестные, aij — коэффициенты при неизвестных, bi — свободные коэффициенты (i = 1 . . . m, j = 1 . . . n). Система из m линейных уравнений с n неизвестными может быть описана при помощи матриц: A · x = b, где x — вектор неизвестных, A — матрица коэффициентов при неизвестных или матрица системы, b — вектор свободных членов системы или вектор правых частей. Совокупность всех решений системы (x1, x2, . . . , xn) называется множеством решений или просто решением системы.
Существует несколько методов решения систем линейных алгебраических уравнений (СЛАУ), и выбор конкретного метода зависит от размера системы, ее характеристик, численных свойств матрицы системы, а также требуемой точности и скорости вычислений.
Некоторые из наиболее распространенных методов решения СЛАУ включают в себя:
-
Метод Крамера. -
Метод Гаусса. -
Метод обратной матрицы. -
Метод Якоби.
Также в задании необходимо высчитать обратную исходной матрице. Обратной матрицей по отношению к данной называется матрица того же типа, которая, будучи умноженной как слева, так и справа на данную матрицу, в результате даст единичную матрицу.
Задание 1.1.
Для решения СЛАУ в системе компьютерной математики Scilab существует специальная матричная функция linsolve(A,b), которая решает систему линейных алгебраических уравнений вида
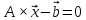
Необходимо решить уравнение вида:
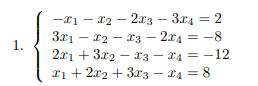
Приводим данное уравнение к виду
 и используем матричную функцию для его решения. (Рисунок 1)
и используем матричную функцию для его решения. (Рисунок 1)Шаги:
-
Создаем матрицу коэффициентов A и вектор свободных членов b. -
Используем встроенную функцию linsolve для решения СЛАУ. -
Производим проверку A*x+b, если в результате получился вектор, достаточно близкий к 0, то решение верно.

Рисунок 1. Решение СЛАУ с помощью встроенной функции.
Так же можно пойти другим способом и реализовать один из классических методов решения СЛАУ в Scilab, например, метод Крамера. (Рисунок 2)
Шаги:
-
Создаем матрицу коэффициентов A и массив свободных членов b. -
Создаем четыре вспомогательные матрицы. (Матрицы, в которых соответствующий столбец заменен на вектор b) -
Высчитываем главный определитель D. -
Высчитываем определители вспомогательных матриц d(1, 2, 3, 4) -
Получаем вектор решений x=d/D
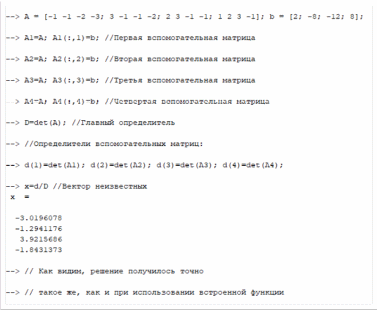
Рисунок 2. Решение СЛАУ методом Крамера в Scilab.
Также для проверки можно подставить значения x в исходное уравнение. (Рисунок 3)

Рисунок 3.
Результат выполнения задания 1.1.
В результате получилось решение системы: x = -3.0196078
-1.2941176
3.9215686
-1.8431373
Задание 1.2.
Если возможно, вычислить матрицу, обратную к матрице D. Обратной матрицей по отношению к данной называется матрица того же типа, которая, будучи умноженной как слева, так и справа на данную матрицу, в результате даст единичную матрицу.
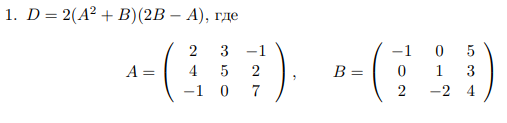
Шаги:
-
Создаем матрицы A и B. -
По формуле высчитываем матрицу D. -
Используем функцию inv для получения обратной матрицы. -
Производим проверку, при умножении обратной матрицы на исходную должна получиться матрица, близкая к единичной.
Ё
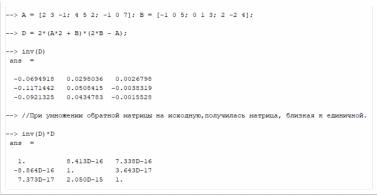
Рисунок 4. Нахождение обратной матрицы.
Результат выполнения задания 1.2.
В результате получилась обратная матрица:
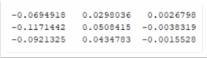
Рисунок 5. Обратная матрица.
Вывод.
В ходе выполнения лабораторной работы было проведено ознакомление с системой компьютерной математики Scilab и ее инструментами для работы с матрицами. Так же было проведено решение СЛАУ в Scilab методом Крамера и с использованием встроенной функции. Так же было выполнено решение задания по нахождению обратной матрицы.