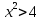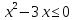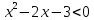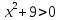Файл: Урока по математике по теме Неравенства и системы линейных неравенств.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МБОУ «Карасаевская СОШ»
Конспект открытого урока по математике
по теме «Неравенства и системы линейных неравенств». Подготовка к ОГЭ.
9 класс.
Разработала урок: учитель математики
Красильникова О.А
План-конспект урока.
Место урока: организация повторения при подготовке к ОГЭ по математике по темы «Решение линейных неравенств с одной переменной и их систем».
Тип урока: урок обобщения изученного материала.
Оборудование: компьютер, мультимедийный проектор, презентация, раздаточный материал, задания для выполнения на уроке, технологические карты урока.
Цель: обобщить и оценить знания учащихся по теме «Неравенства и системы линейных неравенств».
Задачи:
-
Образовательная (формирование познавательных УУД):
-повторить и закрепить учебный материал по теме «Решения линейных неравенств с одной переменной и их систем»; контроль приобретённых знаний.
-
Развивающая (формирование регулятивных УУД):
-
развивать приёмы мыслительной деятельности, внимание; -
формировать потребность к приобретению знаний;
-развивать коммуникативную и информационную компетенции учащихся.
-
Воспитательная: (формирование коммуникативных и личностных УУД):
-воспитывать культуру коллективной работы;
-развитие самостоятельности.
-
знать и понимать алгебраическую трактовку отношений «больше» и «меньше» между числами; -
знать и применять свойства числовых неравенств; -
знать и понимать термины «решение неравенства с одной переменной», «решение системы неравенств с одной переменной»; -
решать линейные неравенства с одной переменной и их системы; -
систематизировать знания и умения учащихся.
| Планируемые образовательные результаты | ||||||||
| Предметные | Метапредметные | Личностные | ||||||
| Владение символьным языком математики, овладение навыками выполнения устных, письменных вычислений. Уметь применять полученные знания при решении задач. | Умение выдвигать гипотезу при решении учебной задачи, понимать необходимость её проверки Умение применять полученные знания в учебной деятельности. Умение действовать в соответствии с предложенным алгоритмом. . | Формировать ответственное отношение к обучению, готовность к саморазвитию и самообразованию на основе мотивации к обучению и познанию. Умение правильно излагать свои мысли, понимать смысл поставленной задачи; Внимательность и аккуратность в вычислениях; требовательное отношение к себе и своей работе. | ||||||
| № | Этап урока | Время | Задачи этапа | Деятельность учителей | Деятельность учащихся | УУД | ||
| 1 | Организационный момент. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся. | 3мин | Обеспечение мотивации учения детьми, постановка цели и задач урока благоприятный психологический настрой на работу. Обеспечение мотивации уче. ния детьми, постановка цели и задач урока | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. Учитель приветствует учащихся, проверяет их готовность к уроку. -- Доброе утро, друзья мои! Я очень рада видеть вас. Сегодня мы принимаем гостей, это своего рода праздник. Настроение должно быть праздничным. Но утром каждый из вас сегодня проснулся со своим настроением. А каким было это настроение? Олег, с каким ты сегодня проснулся настроением? Посмотрите, ребята, у каждого было настроение свое: отличное, хорошее, не очень хорошее. Как же связано настроение с нашим сегодняшним уроком, с математикой? Математика тесно связана с жизнью, только жизненные ситуации переведены на язык символов. Если мы с вами сказали, что с утра мы по своему настроению не одинаковые, разные, не равные, так о чем мы с вами будем говорить сегодня на уроке? О неравенствах, правильно. Несмотря на то, что мы с вами разные, неодинаковые, но тем не менее мы каждый день должны с вами собираться, общаться, учиться, взаимодействовать. Раз мы все месте с вами собрались, то мы как неравенства объединились во что? В систему. Нам осталось сформулировать тему нашего урока. Какую цель нужно поставить перед собой на уроке? Также сегодня вы сделаете очередной шаг навстречу большой цели – итоговая аттестация. Я с радостью помогу вам сделать этот шаг. . | Включаются в деловой ритм урока. Учащиеся слушают учителя, подписывают листы самооценивания и технологические карты. «Решения линейных неравенств с одной переменной и их систем». Наша цель на уроке – обобщить знания и закрепить учебный материал по теме «Решения линейных неравенств с одной переменной и их систем». Повторить, проверить, закрепить, систематизировать, сделать выводы. | Коммуникати вные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные : организация своей учебной деятельности. Личностные: мотивация учения. | ||
| 2 | Актуализациязнаний | 1 мин | Актуализация опорных знаний и способов действий. | “Корзина” знаний На столе стоит «корзина» знаний, в которой условно будет собрано все то, что все ученики вместе знают об изучаемой теме. | Формулируют тему и цель урока, задачи. Записывают в тетради дату и тему урока | Коммуникати вные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные : организация своей учебной деятельности. Познавательн ые: структурирова ние собственных знаний. | ||
| | Повторение теории. Подготовка к обобщению. Обобщениеисистематизациязнаний(продолжение) Физминутка (сменить деятельность, обеспечить эмоциональную разгрузку) Обобщениеисистематизациязнаний. Самостоятельная работа | 5 мин | | Решение теста
1) Является ли число 12 решением неравенства 2х>10? 2) Является ли число - 6 решением неравенства 4х>12? 3) Является ли неравенство 5х-15>4х+14 строгим? 4) Существует ли целое число, принадлежащее промежутку [-2,8; -2,6]? 5) При любом ли значении переменной а верно неравенство а² +4 >о? 6) Верно ли, что при умножении или делении обеих частей неравенства на отрицательное число знак неравенства не меняется? 7) Верно ли, что при переносе слагаемых из одной части неравенства в другую знак неравенства не меняется? Проверка 1010100
Установите соответствие между неравенствами и числовыми промежутками: 1. 3x > 6 а) (-∞ ; - 0,2] 2. -5х ≥ 1 б) (-∞ ; 15) 3. 4х > 3 в) ( 2; + ∞ ) 4. 0,2х < 3 г) ( 0,75; +∞ ) Ребята что нам нужно повторить? Ребята что такое неравенство? А что значит решить неравенство? А какие бывают неравенства? (Линейные,квадратные,строгие,нестрогие) Какие существуют способы решения неравенств? (Метод параболы,метод интервалов) Решение линейных неравенств 1. ????????−????≥−????????−5 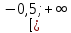 2.????????+????≥????????−???? 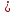 3.????????−????>????−????(????-2) 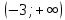 4. 3(2х-4)≤-5(2-3х), 5. 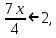 6. 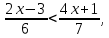 7. 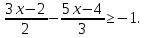 Решение неравенств второй степени 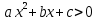 или или 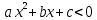
Метод интервалов
Решение неравенств второй степени Приступаем крешению системлинейныхнеравенств. Учитель напоминает, что если каждое из неравенств в системе является линейным неравенством, то говорят, что задана система линейных неравенств с одной переменной. Решением системы неравенств называют такое значение переменной, при котором неравенства системы преобразуются в верные числовые неравенства. Решить систему неравенств – найти все её решения или доказать, что решений нет. Решение систем неравенств
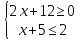 1) 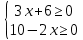 2) 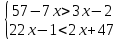 1) 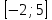 2) 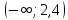 Самостоятельная работа(Приложение 2) «5» – 4 задания «4» – 3 задания «3» – 2 задания Дополнительное задание: решить систему неравенств 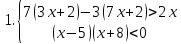 2. 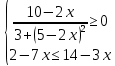 | Выполняют тест. Взаимная проверка Индивидуальная работа Групповая работа Свойства неравенств Какие бывают неравенства и как их решать Что является решением неравенства и системы неравенств Неравенства получаются равносильные, если 1. Перенести с противоположным знаком слагаемое из одной части неравенства в другую 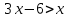 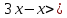 6 62. Умножить или разделить обе части неравенства на одно и тоже положительное число 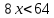 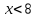 3. Умножить или разделить обе части неравенства на одно и тоже отрицательное число, изменив при этом знак неравенства на противоположный 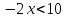 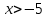 Называют свойства неравенств, которыми пользуются при решении. Записывают решение. Отвечают на вопросы учителя. Участвуют в беседе с учителем, отвечают на вопросы. Отвечают напоставленныйвопрос Называют свойства неравенств, которыми пользуются при решении. Записывают решение. Отвечают на вопросы учителя. Проверяют правильность своего решения, находят допущенные ошибки. Индивидуальная работа | формирование интереса к данной теме. Личностные: формирование готовности к самообразованию. Коммуникативные: уметь оформлять свои мысли в устной форме; слушать и понимать речь других. Регулятивные: планирование своей деятельности для решения поставленной задачи и контроль полученного результата. Фронтальная, индивидуальная работа Познавательные: Структурирование собственных знаний по теме «Решение линейных неравенств и систем неравенств с одной переменной» Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и сверстниками. Регулятивные: контроль и оценка процесса и результатов деятельности. Личностные: оценивание усваиваемого материала. Коммуникати вные: умение слушать и вступать в диалог; воспитывать чувство взаимопомощи, уважительное отношение к чужому мнению, культуру учебного труда. Личностные: формирование внимательност и и аккуратности в вычислениях, требовательное отношение к себе и своей работе. Регулятивные : умение самостоятельн о формулировать новые учебные задачи путем задавания вопросов о неизвестном; планировать собственную деятельность, определять средства для ее осуществления Личностные: формирование позитивной самооценки Регулятивные: умение самостоятельно адекватно анализировать правильность выполнения действий и вносить необходимые коррективы. |
| Домашнее задание Итог занятия Рефл | | Обеспечение понимания детьми содержания и способов выполнения домашнего задания. | Дает комментарий к домашнему заданию. По результатам самостоятельной работы «2» - работа над ошибками своего варианта + ещё 2 варианта «3» - работа над ошибками своего варианта + ещё 1 вариант «4-5» - Решить неравенство: а) 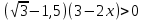 б) 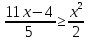 Решить систему неравенств: 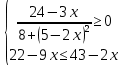 | Учащиеся записывают в дневники задание | | |
| Итог занятия Рефлексия | | Информация о домашнем задании |
Я предлагаю вам закончить предложения: «Сегодня на уроке Я повторил … Я закрепил….. Мне предстоит повторить.... Учитель оценивает учащихся, отмечает лучших. | Отвечают на вопросы. Рассказывают, что узнали. Дают самооценку уровню приобретенных знаний. | Регулятивные: оценивание собственной деятельности на уроке |
| | | | . | |
| | | | | | | | Познавательн ые: Поиск и выделение необходимой информации. Структурирова ние знаний. Анализ заданий. Регулятивные : Целеполагание, |
| 4 | | | | | | | |
| | | | | | | | |
| | | | | | | | |
| | | ||||||
| | | | | | | | |
| | | | | | | |
| | | | | | | |
Приложение 1
Приложение 2
Приложение 3
Приложение 1
Продолжите фразы:
Сегоднянаурокеяповторил


Сегоднянаурокеязакрепил


Мнепредстоитповторить


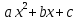
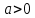 и вниз при
и вниз при 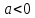 )
)